Mathématiques 6e
Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Mes Pages
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 13
Pas à pas
2. Volume d'un pavé droit
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
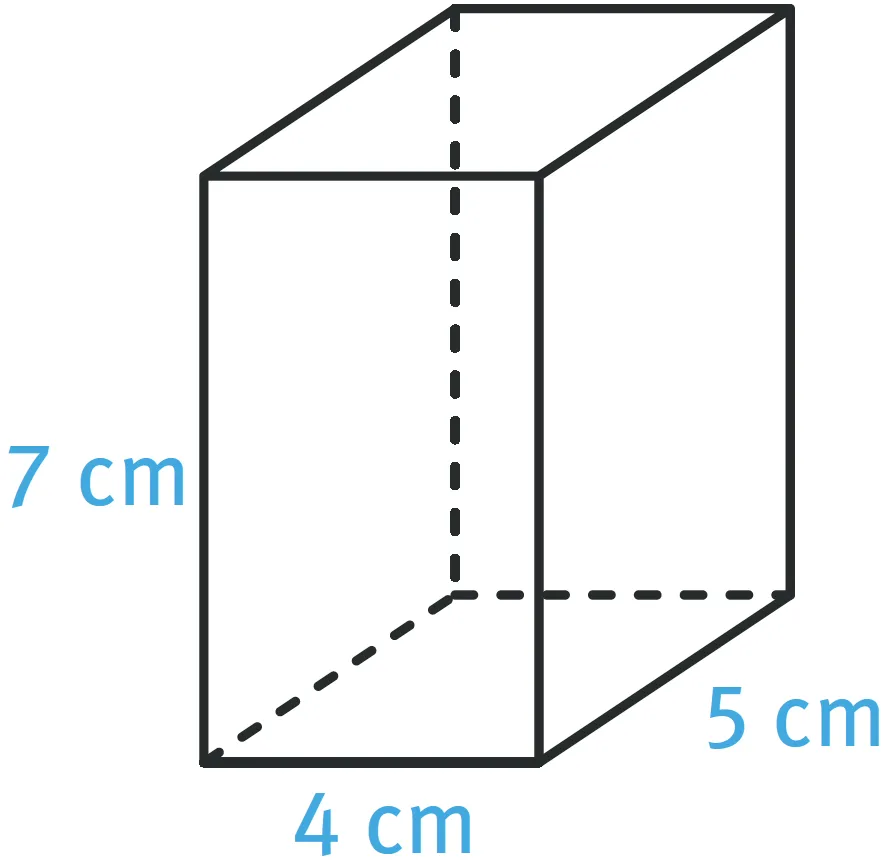
a. Combien de cubes de 1 cm d'arête peut-on placer « au fond » de ce pavé droit ?
b. Combien de couches peut-on ainsi placer ?
c. Combien de cubes de 1 cm de côté peut-on donc placer au maximum dans ce pavé ?
b. Combien de couches peut-on ainsi placer ?
c. Combien de cubes de 1 cm de côté peut-on donc placer au maximum dans ce pavé ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
- Le volume d'un solide mesure l'espace qui est contenu dans ce solide.
- Pour mesurer un volume, on utilise souvent les unités de mesure suivantes :
- le centimètre cube (cm^3) : le volume d'un cube d'un centimètre d'arête ;
- le décimètre cube (dm^3) : le volume d'un cube d'un décimètre d'arête ;
- le mètre cube (m^3) : le volume d'un cube d'un mètre d'arête.
- On utilise aussi souvent les unités de contenance, qui mesurent la quantité de liquide que peut contenir un volume. L'unité de contenance de base est le litre, on en déduit alors :
- le décilitre : un dixième de litre ;
- le centilitre : un centième de litre ;
- le millilitre : un millième de litre.
- On utilise rarement des unités de volume plus grandes que le mètre cube, mais il en existe aussi :
- le décamètre cube : le volume d'un cube d'un décamètre d'arête ;
- l'hectomètre cube : le volume d'un cube d'un hectomètre d'arête ;
- etc.
- Comme on le voit dans le tableau précédent, les unités de volume varient de 1 000 en 1 000 : 1 m^3 = 1 000 dm^3. Les unités de contenance varient de 10 en 10 : 1 L = 10 dL.

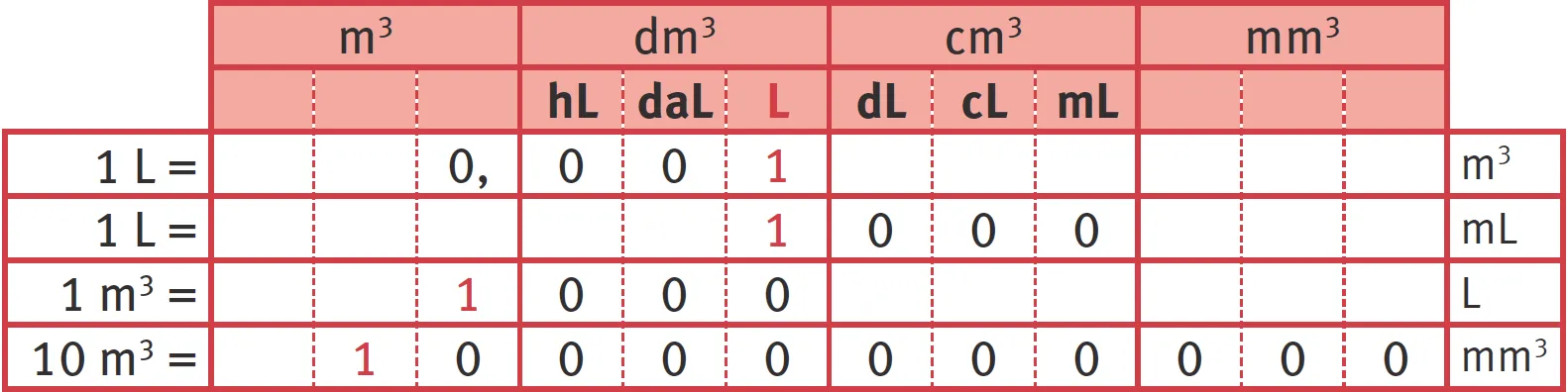
hL = hectolitre ; daL = décalitre ; L = litre ; dL = décilitre ; cL = centilitre ; mL = millilitre.
Remarques :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Convertir une mesure de volume en mesure de contenance
Exprimer 15,2 dm^3en cL.
- On rappelle que 1 dm^3 = 1 L et 1 L = 100 cL.
- Donc 15,2 dm^3 = 15,2 \times 100 cL = 1 520 cL.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4Conversions
1. Exprimer 267 dm3 en hL.
2. Exprimer 35,4 cm3 en cL.
3. Exprimer 482 mm3 en mL.
4. Exprimer 324 L en m3.
5. Exprimer 32,5 cL en mm^3.
6. Exprimer 247 dL en cm3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
- Quand on calcule un volume, il faut exprimer les grandeurs dans une même unité, en respectant la règle :
- m \times m \times m \rightarrow m^3
- dm \times dm \times dm \rightarrow dm^3
- cm \times cm \times cm \rightarrow cm^3
Exemple : 3 cm \times 5 cm \times 8 cm = (3 \times 5 \times 8) cm^3 = 120 cm^3.
- Le volume d'un parallélépipède rectangle est le produit des trois dimensions.
- Si le parallélépipède a des arêtes de longueur a, b et c son volume V vaut :
- V = a \times b \times c

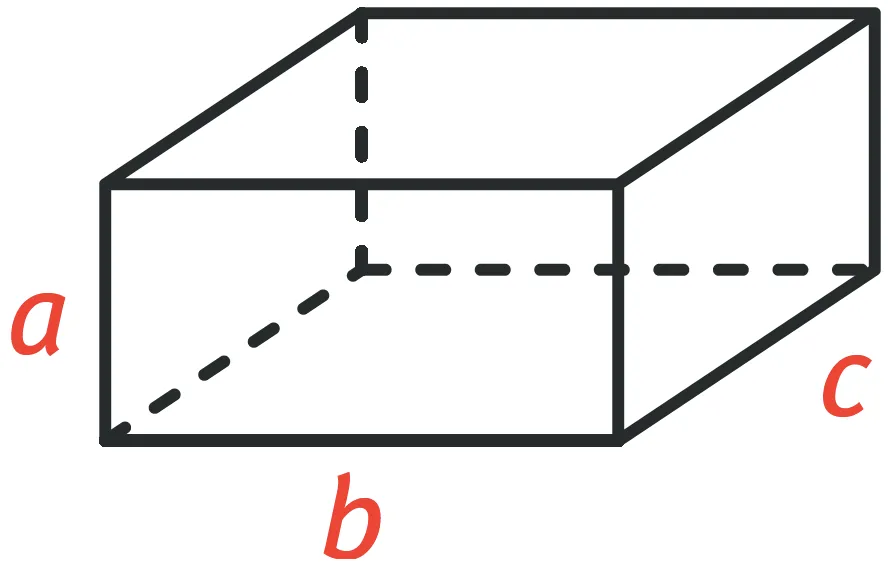
- Un cube d'arête de longueur c a un volume de c \times c \times c.
Exemples :
- Un parallélépipède rectangle de dimension 4 cm par 5 cm par 9 cm a un volume de 4 cm \times 5 cm \times 9 cm = (4 \times 5 \times 9) cm^3 = 180 cm^3.
- Si un cube a des arêtes de longueur 3 cm, son volume est 3 cm \times 3 cm \times 3 cm = (3 \times 3 \times 3) cm^3 = 27 cm^3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Calculer le volume d'un pavé droit avec son patron
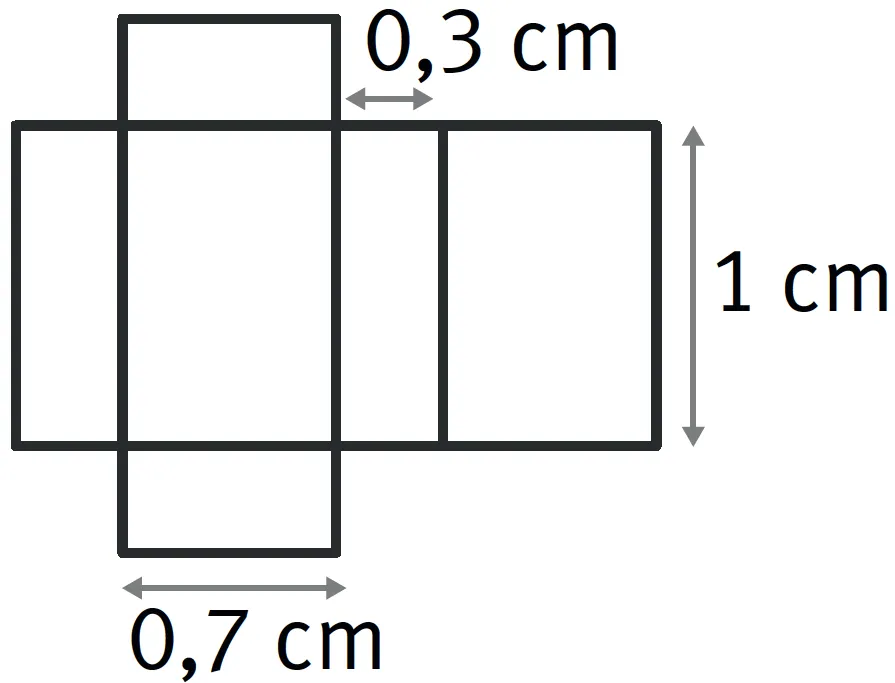
Quel est le volume du parallélépipède dont on donne ici le patron ?
- On mesure les longueurs sur le patron.
- On calcule : 1 cm \times 0,7 cm \times 0,3 cm = (1 \times 0,7 \times 0,3) cm^3 = 0,21 cm^3.
- Le volume est de 0,21 cm^3.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
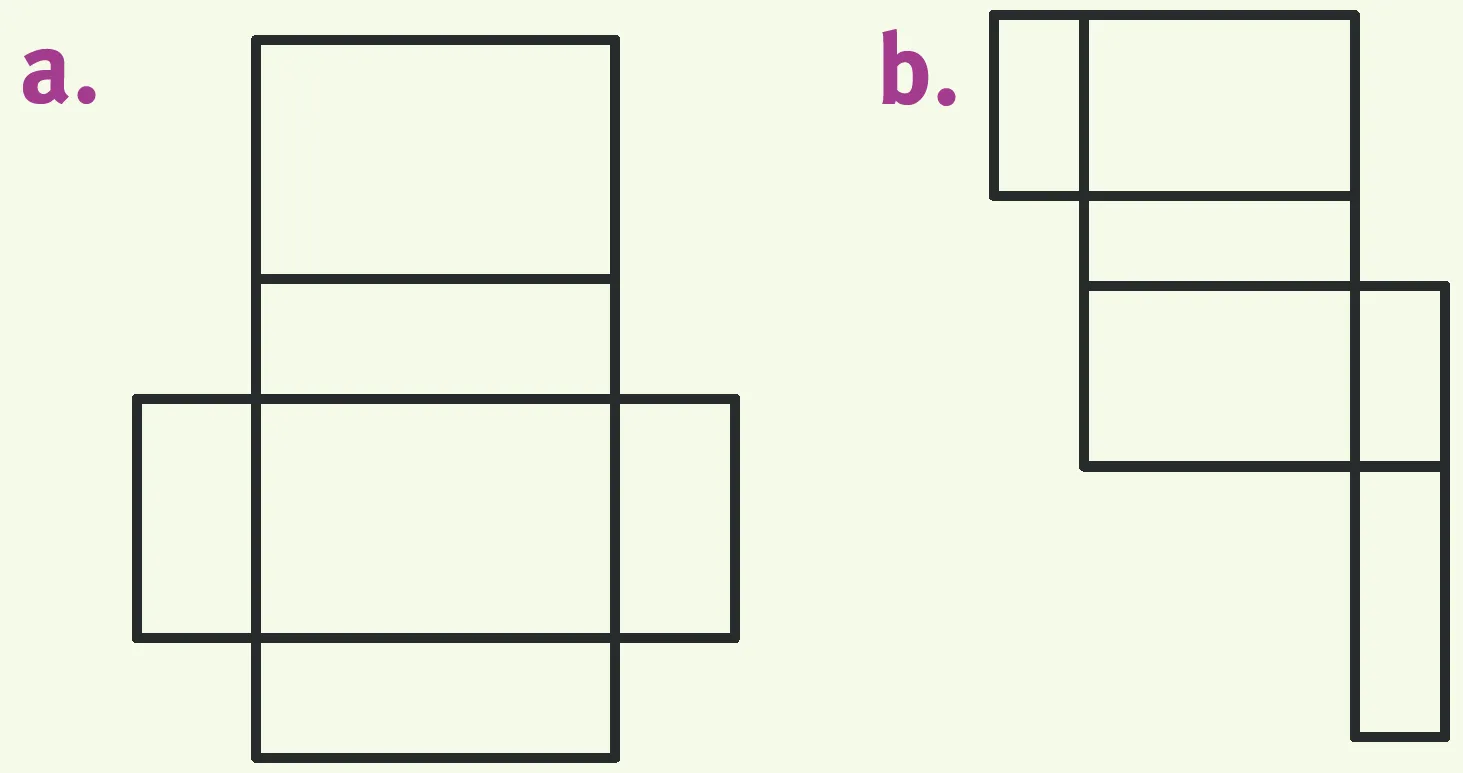
Exercice 5Donner le volume de chaque parallélépipède rectangle dont on donne le patron

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6Donner le volume d'un pavé de dimensions...
1. 4 cm par 8 cm par 7 cm ;
2. 3,2 km par 1,8 km par 0,5 km ;
3. 120 m par 18 m par 45 m ;
4. 14 mm par 18 mm par 23 mm ;
5. 15 hm par 3,5 hm par 6,3 hm.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
