Mathématiques 6e

Rejoignez la communauté !

Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.

Du primaire au collège

Ch. 1

Manipuler les nombres entiers

Ch. 2

Les nombres décimaux

Ch. 3

Addition, soustraction

Ch. 4

Multiplication, division décimale

Ch. 5

Fractions

Ch. 6

Proportionnalité

Ch. 7

Construction de droites

Ch. 8

Distances et cercles

Ch. 9

Angles

Ch. 10

Symétrie axiale

Ch. 11

Triangles, rectangles et losanges

Ch. 12

Aire et périmètre

Ch. 13

Volumes

Chapitre 5

Exercices

Fractions

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Échauffement

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

11

Écrire chaque nombre en écriture fractionnaire.

1. Un demi.

2. Quatre tiers.

3. Sept quarts.

4. Trois cinquièmes.

5. Cent sixièmes.

6. Huit septièmes.

7. Vingt huitièmes.

8. Neuf neuvièmes.

9. Quinze dixièmes.

10. Quarante centièmes.

11. Soixante-huit millièmes.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14

Écrire les fractions suivantes en toutes lettres.

1.

\frac{1 2}{4}

\frac{5}{3}

\frac{5}{2}

\frac{1 2 8}{7}

\frac{3 2 1}{1 0}

\frac{5 5}{1 0 0}

\frac{1 3 5 4}{1 0 0 0}

\frac{9 8}{9}

\frac{4 5}{8}

10.

\frac{3 6}{5}

11.

\frac{7}{6}

12.

\frac{1 8}{2 0}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15
Pour chaque forme

1. Donner la fraction représentée par la partie colorée 1.

Le zoom est accessible dans la version Premium.

2. Donner la fraction représentée par la partie colorée 2.

Le zoom est accessible dans la version Premium.

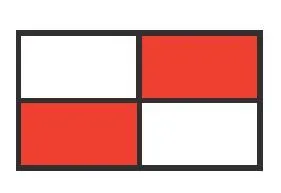
3. Donner la fraction représentée par la partie colorée 3.

Le zoom est accessible dans la version Premium.

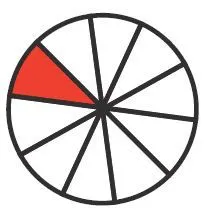4. Donner la fraction représentée par la partie colorée 4.

Le zoom est accessible dans la version Premium.

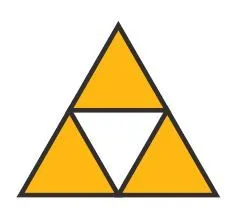
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16

Donner la forme décimale des fractions suivantes.

\frac{2 3 8}{1 0}

\frac{9 8 4}{1 0 0}

\frac{4 5}{1 0 0 0}

\frac{4 7 8}{1 0 0 0 0}

\frac{5}{1 0}

\frac{4 7 4}{1 0 0}

\frac{5 4 7}{1 0 0}

\frac{8 7 9 4}{1 0}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

17

Compléter avec la valeur correspondante.

\frac{7}{3} = \frac{2 1}{. . .}

\frac{8}{1 2} = \frac{1 6}{. . .}

\frac{1 4}{5} = \frac{. . .}{2 0}

\frac{8}{1 3} = \frac{. . .}{2 6}

\frac{. . .}{4 2} = \frac{7}{2 1}

\frac{. . .}{1 8} = \frac{7}{6}

\frac{5 2}{. . .} = \frac{1 3}{1 7}

\frac{6 5}{. . .} = \frac{5}{2}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

18

Compléter avec la valeur correspondante.

\frac{4 2}{1 8} = \frac{. . .}{6}

\frac{2 5}{1 0} = \frac{. . .}{2}

\frac{3 6}{1 5} = \frac{1 2}{. . .}

\frac{4 9}{2 1} = \frac{7}{. . .}

\frac{. . .}{5} = \frac{6 4}{4 0}

\frac{. . .}{1 1} = \frac{6 3}{9 9}

\frac{6}{. . .} = \frac{6 6}{3 3}

\frac{8}{. . .} = \frac{5 6}{2 1}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

19
Critères de divisibilité

1. 8 et 24 sont-ils pairs ? Pourquoi ? Compléter les pointillés :

\frac{8}{2 4} = \frac{. . . \times 2}{. . . \times 2} = \frac{. . .}{. . .}

2. 15 et 25 sont-ils des multiples de 5 ? Compléter les pointillés :

\frac{2 5}{1 5} = \frac{. . . \times 5}{. . . \times 5} = \frac{. . .}{. . .}

3. 49 et 56 sont-ils des multiples de 7 ? Compléter les pointillés :

\frac{5 6}{4 9} = \frac{. . . \times 7}{. . . \times 7} = \frac{. . .}{. . .}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

20

Sur l'axe gradué correspondant, placer les fractions proposées avec l'outil de dessin.

Dessinez ici

\frac{1}{6}

;

\frac{4}{6}

;

\frac{7}{6}

\frac{1}{1 4}

;

\frac{1}{7}

;

\frac{3}{7}

\frac{1}{3}

;

\frac{2}{3}

;

\frac{4}{3}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

21

Effectuer de tête les calculs suivants.

\frac{3}{5} \times 20

\frac{7}{4} \times 16

\frac{2 1}{7} \times 70

\frac{4}{9} \times 99

\frac{5}{1 2} \times 60

\frac{1 8}{9} \times 4

\frac{1}{2} \times 9

\frac{1}{3} \times 15

\frac{7}{8} \times 32

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

22

Écrire sous forme de fraction les nombres suivants et les comparer à 1.

1. 31 %

2. 45 %

3. 17,7 %

4. 185 %

5. 9 412 %

6. 0,73 %

7. 78 %

8. 100 %

9. 400 %

10. 1 000 %

11. 99,9 %

12. 1 100 %

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

23

Écrire sous forme de la somme d'un entier et d'une fraction inférieure à 1 les fractions suivantes.

1.

\frac{1 8}{5}

\frac{2 9}{7}

\frac{3 6}{1 1}

\frac{5 9}{8}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

24

Encadrer les fractions suivantes par deux entiers consécutifs.

1.

\frac{2 7}{6}

\frac{3 9}{8}

\frac{4 7}{5}

\frac{6 8}{9}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Entraînement

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

26
Qui suis-je ?

Je sais juste que je suis une fraction.

1. Je suis égale à

\frac{8}{3}

et mon numérateur est 24.

2. Je suis égale à

\frac{7}{4}

et mon numérateur est pair et inférieur à 15.

3. Je suis égale à

\frac{3 5}{4 5}

et mon dénominateur est le cinquième de 45.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

27
Quelle écriture en toutes lettres correspond à quelle fraction ?

Relis chaque valeur à sa prononciation.

$\frac{3}{1 7}$
$\frac{1 3}{1 5}$
$\frac{1 5}{3}$
$\frac{1 7}{3}$

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

28
Quelle écriture en toutes lettres correspond à quelle fraction ?

Compléter Le tableau suivant.

Écriture en français	Calcul à poser	Résultat
Un tiers de neuf
Trois-quarts de dix-huit et trois dixièmes
Cinq sixièmes de quinze et six dixièmes
	$\frac{7}{8} \times 12, 7$
	$\frac{1 3}{1 5} \times 8, 4$
		5,6

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

29

Calculer.

\frac{9}{7} \times 6, 3

\frac{1 7}{3 7} \times 2, 22

\frac{1 5}{4} \times 0, 871

\frac{7}{1 2} \times 18, 36

\frac{8 9}{3 6} \times 26, 1

\frac{4}{9} \times 3, 51

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

30

Comparer chaque fraction à 1

\frac{8}{2}

\frac{1 7}{3}

\frac{2}{7}

\frac{9}{2 5}

\frac{3 6}{3 6}

\frac{8}{9}

\frac{9}{8}

\frac{6}{4}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

31

Pour comparer

\frac{8}{1 7}

3

on utilise

3 = \frac{3}{1} = \frac{5 1}{1 7}

1. Comparer

\frac{9}{4}

2

2. Comparer

\frac{2 5}{5}

5

3. Comparer

\frac{9}{2}

4

4. Comparer

\frac{8}{7}

4

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

32

Pour chacune des fractions suivantes, dire si elle représente un nombre entier et en donner une valeur approchée par excès au millième.

1. Treize septièmes.

2. Quinze tiers.

3. Seize quarts.

4. Trois cinquièmes.

5. Douze neuvièmes.

6. Deux tiers.

7. Vingt-quatre quinzièmes.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

33

Placer des fractions sur un demi-axe.

Le zoom est accessible dans la version Premium.

1. Victor a reçu une tablette de chocolat pour Pâques et veut la faire durer une semaine. Quelle fraction de la tablette mangera-t-il chaque jour ?

2. Victor reçoit une deuxième tablette mais continue de manger la même quantité de chocolat chaque jour. Dessiner un demi-axe gradué et y placer les quantités de chocolat mangées au 4

^{e}

jour,au 9

^{e}

jour et au 14

^{e}

jour.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

34
On donne l'axe gradué ci-contre

Le zoom est accessible dans la version Premium.

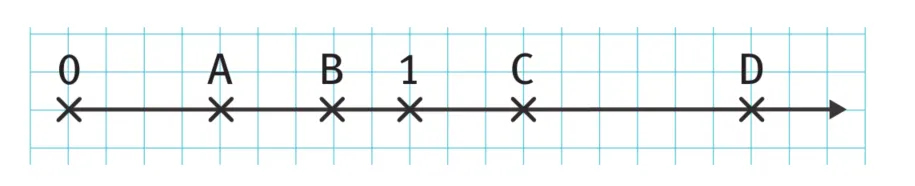
Donner sous forme de fractions les points représentés.

Comment peut-on écrire plus simplement les fractions représentant les points C et D ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

35
On donne l'axe gradué ci-contre

Recopier l'axe gradué suivant

Le zoom est accessible dans la version Premium.

1. Peut-on placer directement les fractions

\frac{2}{1 4}

\frac{6}{1 4}

\frac{1 6}{1 4}

sur l'axe suivant ? Pourquoi ? Si c'est le cas, les placer.

2. Peut-on placer la fraction

\frac{5}{1 4}

sur cet axe sans modifier les graduations ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

36
Avec des lettres

On donne les nombres suivants :

x = 15

y = 6

a = 8

b = 10

. Écrire et simplifier si possible les fractions suivantes.

\frac{x}{y}

Fractions

Échauffement

11

14

15Pour chaque forme

16

17

18

19Critères de divisibilité

20

21

22

23

24

Entraînement

25Vrai ou faux ?

26Qui suis-je ?

27Quelle écriture en toutes lettres correspond à quelle fraction ?

28Quelle écriture en toutes lettres correspond à quelle fraction ?

29

30

31

32

33

34On donne l'axe gradué ci-contre

35On donne l'axe gradué ci-contre

36Avec des lettres

15
Pour chaque forme

19
Critères de divisibilité

25
Vrai ou faux ?

26
Qui suis-je ?

27
Quelle écriture en toutes lettres correspond à quelle fraction ?

28
Quelle écriture en toutes lettres correspond à quelle fraction ?

34
On donne l'axe gradué ci-contre

35
On donne l'axe gradué ci-contre

36
Avec des lettres