Mathématiques 6e
Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Mes Pages
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 5
Pas à pas
1. Présentation des fractions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADéfinition
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
DécouvrirDe la fraction « partage » à la fraction « quotient » : le guide-âne
a. Observer le guide-âne. On pourra le prolonger si nécessaire.


b. Tracer un demi-axe et y repérer une unité.
c. Diviser cette unité en 7 grâce au guide-âne. Quelle fraction obtient-on ?
d. Reporter 8 fois cette portion. Quelle fraction obtient-on ?
e. Reporter 8 fois l'unité pour représenter 9.
f. Diviser le segment de longueur 9 unités en 7 grâce au guide-âne. Quelle fraction obtient-on ?


b. Tracer un demi-axe et y repérer une unité.
c. Diviser cette unité en 7 grâce au guide-âne. Quelle fraction obtient-on ?
d. Reporter 8 fois cette portion. Quelle fraction obtient-on ?
e. Reporter 8 fois l'unité pour représenter 9.
f. Diviser le segment de longueur 9 unités en 7 grâce au guide-âne. Quelle fraction obtient-on ?
- Effectuer 9 \div 7 avec une calculatrice. Qu'obtient-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
- Une fraction peut être vue de trois manières différentes.
- Comme une proportion.
- La fraction \dfrac{9}{7} : on a divisé une quantité en 7 portions. Chaque portion représente \dfrac{1}{7}. 9 portions représentent {9 \times \dfrac{1}{7} = \dfrac{9}{7}}.
- Comme un nombre.
- La fraction \dfrac{9}{7} est un nombre dont une valeur approchée au centième est 1,29 : {\dfrac{9}{7} \approx 1 \text{,} 29}.
- Comme un quotient.
- La fraction \dfrac{9}{7} est le quotient de 9 par 7.
- Écrire une fraction, c'est juste écrire différemment un quotient.
Rappels :
- Le quotient de a par b (a \div b) est le nombre qui multiplié par b donne a.
- Ainsi \dfrac{a}{b} = a \div b et b \times \dfrac{a}{b} = a.
- Vocabulaire :

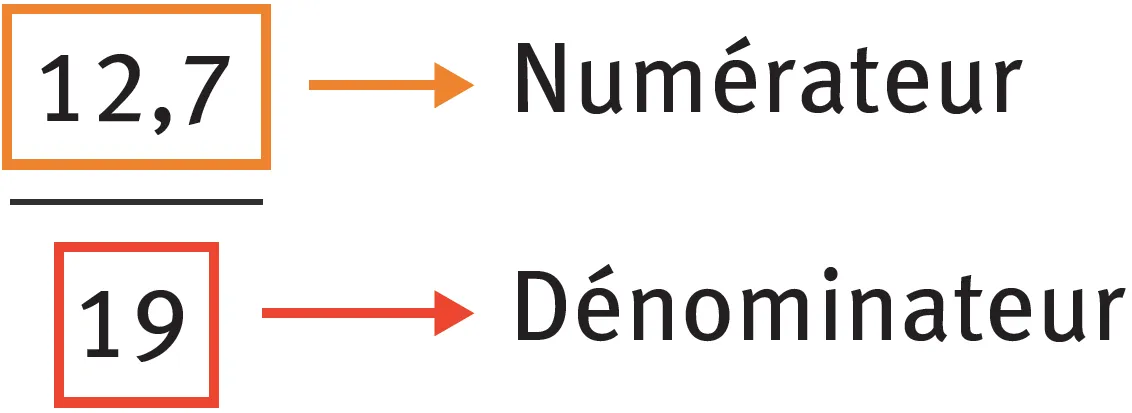
Attention !
Le dénominateur ne peut jamais être nul.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1Vrai ou faux ?
1. Dans la fraction \dfrac{7}{3}, le nombre 7 est le numérateur.
2. 0 \times \dfrac{27}{0} = 27
3. Dans la fraction \dfrac{7}{3}, le nombre 3 est le dénominateur.
2. 0 \times \dfrac{27}{0} = 27
3. Dans la fraction \dfrac{7}{3}, le nombre 3 est le dénominateur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Remarque :
Tout nombre décimal peut s'écrire sous forme de fraction, c'est l'écriture fractionnaire.
Exemple : 2\text{,}57 = \dfrac{257}{100}
Remarque :
Toute fraction n'est pas un nombre décimal. Par exemple \dfrac{1}{7} ne peut s'écrire autrement que \dfrac{1}{7}. Si on en veut une valeur exacte, on est obligé d'en garder une écriture fractionnaire. Par contre, si on en veut une valeur approchée, on peut écrire {\dfrac{1}{7} \approx 0 \text{,} 143}.
Attention !
\dfrac{1}{7} \approx 0 \text{,} 143 n'est pas une égalité !
Remarque :
Si b \neq 0 on a toujours \dfrac{b}{b} = 1 car b \times 1 = b.
Tout nombre décimal peut s'écrire sous forme de fraction, c'est l'écriture fractionnaire.
Exemple : 2\text{,}57 = \dfrac{257}{100}
Remarque :
Toute fraction n'est pas un nombre décimal. Par exemple \dfrac{1}{7} ne peut s'écrire autrement que \dfrac{1}{7}. Si on en veut une valeur exacte, on est obligé d'en garder une écriture fractionnaire. Par contre, si on en veut une valeur approchée, on peut écrire {\dfrac{1}{7} \approx 0 \text{,} 143}.
Attention !
\dfrac{1}{7} \approx 0 \text{,} 143 n'est pas une égalité !
Remarque :
Si b \neq 0 on a toujours \dfrac{b}{b} = 1 car b \times 1 = b.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Donner une écriture décimale d'une fraction
Donner une écriture décimale de la fraction suivante : \dfrac{7}{14}.
- On cherche un nombre x tel que 14 \times x = 7.
- On effectue la division 7 \div 14 qui donne 0,5.
- \dfrac{7}{14} = 0\text{,}5. On a bien 14 \times 0,5 = 7.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2Donner une écriture décimale des fractions suivantes
Vérifier le résultat comme précédemment.
1. \dfrac{2}{4}
2. \dfrac{8}{10}
3. \dfrac{12}{5}
4. \dfrac{17}{4}
5. \dfrac{36}{32}
6. \dfrac{135}{16}
7. \dfrac{4\:712}{32}
8. \dfrac{94}{32}
9. \dfrac{15\:444}{33}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BPlacer une fraction sur un axe gradué
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
- Il existe plusieurs méthodes pour placer une fraction sur un axe. Par exemple, pour placer \dfrac{4}{7} :
- Soit diviser 4 unités en 7.
- Soit diviser 1 unité en 7 et la reporter 4 fois au compas.
- Pour diviser une unité, on peut utiliser au choix :
- Le quadrillage
- Un « guide-âne »
- Une règle graduée
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
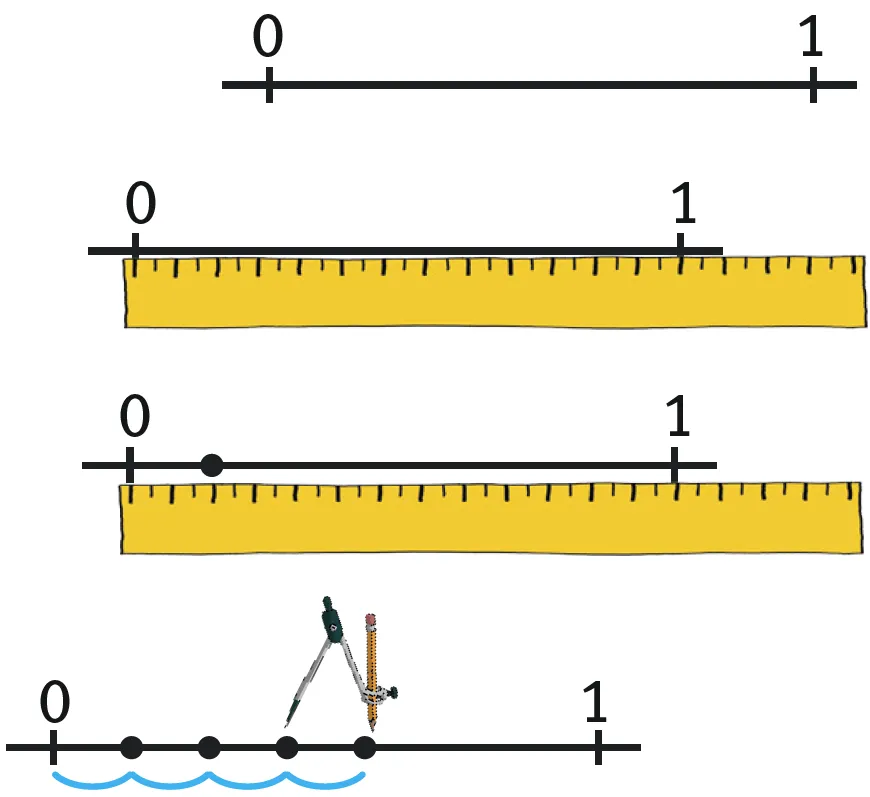
Refaire Partager une unité avec une règle graduée
Partager en 7 l'unité représentée sur l'axe.
- On mesure l'unité : 4,2 cm.
- On divise cette mesure par 7 : 4,2 cm \div 7 = 0,6 cm.
- On place la première graduation à 0,6 cm.
- On reporte la graduation.

Remarque :
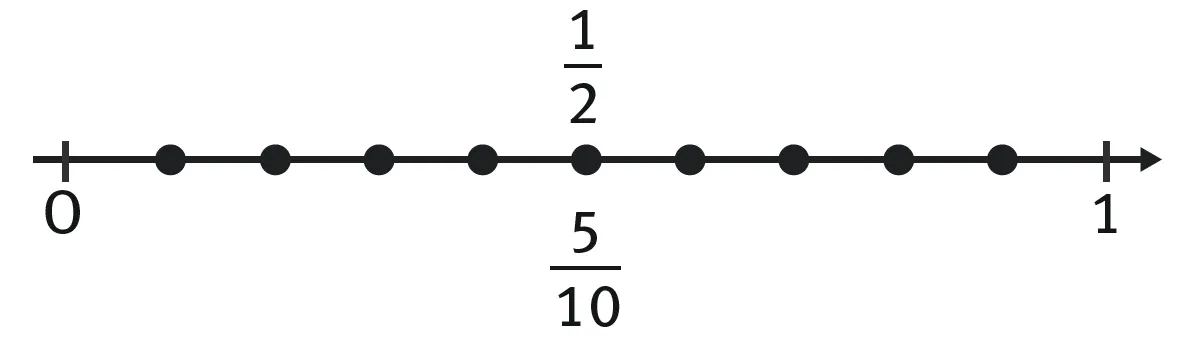
Il est ainsi possible de déterminer l'égalité de deux fractions.
Exemple : \dfrac{1}{2} et \dfrac{5}{10} se placent au même endroit sur la droite, ils sont donc égaux.
Il est ainsi possible de déterminer l'égalité de deux fractions.
Exemple : \dfrac{1}{2} et \dfrac{5}{10} se placent au même endroit sur la droite, ils sont donc égaux.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3Placer les fractions données sur les axes gradués suivants
1. \dfrac{1}{9} ; \dfrac{4}{9} ; \dfrac{6}{9}
2. \dfrac{14}{57} ; \dfrac{16}{57} ; \dfrac{19}{57}
3. \dfrac{1}{3} ; \dfrac{4}{3} ; \dfrac{5}{3}
2. \dfrac{14}{57} ; \dfrac{16}{57} ; \dfrac{19}{57}
3. \dfrac{1}{3} ; \dfrac{4}{3} ; \dfrac{5}{3}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
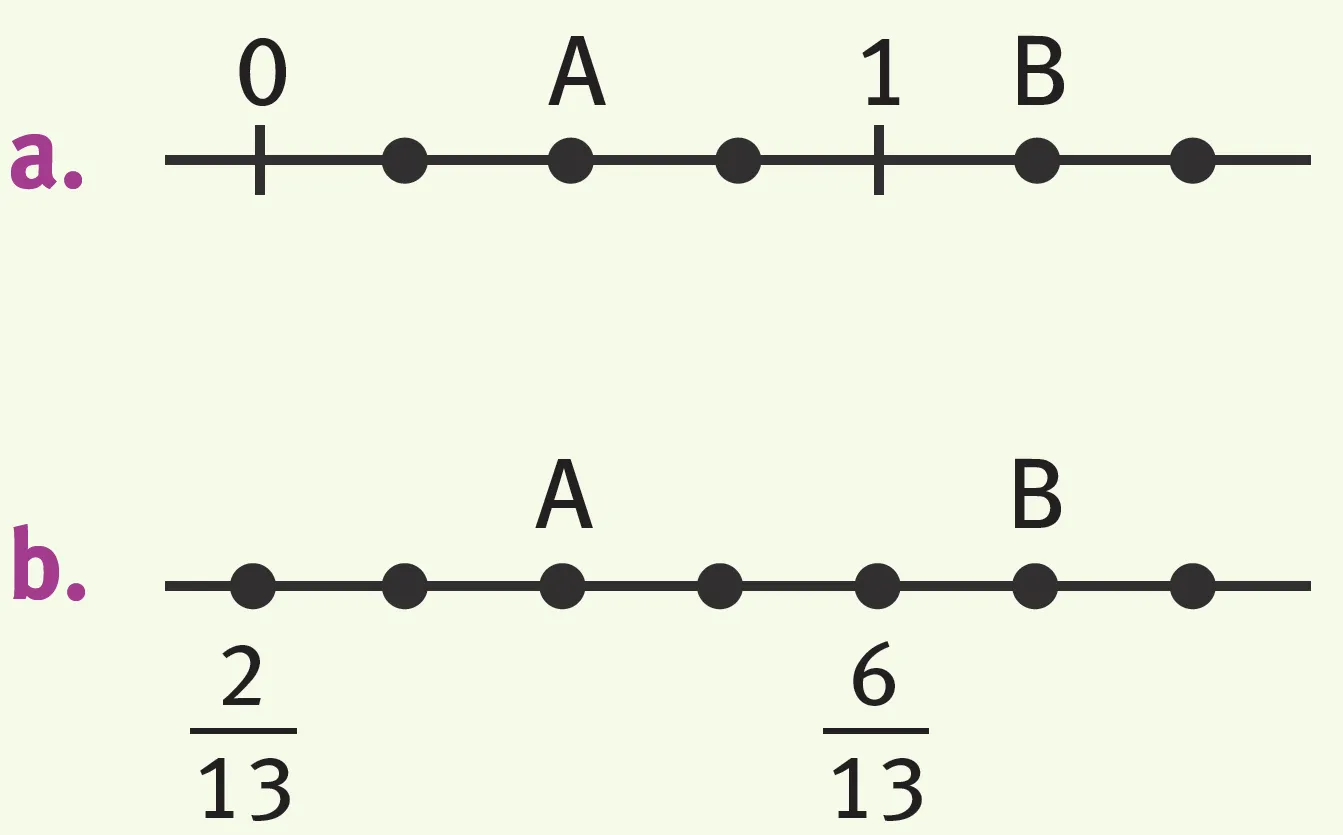
Exercice 4Écrire les nombres A et B sous forme de fraction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5Placer les fractions données sur l'axe gradué
1. \dfrac{3}{4} ; \dfrac{5}{4} ; \dfrac{7}{4}
2. \dfrac{5}{11} ; \dfrac{8}{11} ; \dfrac{19}{11}
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
