Mathématiques Cycle 4

Rejoignez la communauté !

Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.

Thème 1 : Nombres et calculs

Ch. 1

Arithmétique

Ch. 2

Nombres relatifs

Ch. 3

Nombres fractionnaires

Ch. 4

Calcul littéral

Ch. 5

Équations et inéquations

Ch. 6

Proportionnalité

Ch. 7

Puissances

Thème 2 : Organisation et gestion de données

Ch. 8

Statistiques

Ch. 9

Probabilités

Ch. 10

Fonctions

Thème 3 : Grandeurs et mesures

Ch. 11

Grandeurs et mesures

Thème 4 : Espace et géométrie

Ch. 12

Transformations dans le plan

Ch. 13

Triangles

Ch. 14

Angles et droites parallèles

Ch. 15

Géometrie dans l'espace

Ch. 16

Théorème de pythagore

Ch. 17

Agrandissements - réductions

Ch. 18

Trigonométrie

Annexes

Livret algorithmique et programmation

Pistes EPI

Dossier brevet

Chapitre 16

Problèmes résolus

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

41
Un carré

✔ J'envisage plusieurs méthode de résolution
✔ Je comprends la modélisation numérique ou géométrique d'une situation

ABCD

est un carré de côté

10 cm

AE = 2,5 cm

. Le point

F

est le milieu de

[AD]

Le zoom est accessible dans la version Premium.

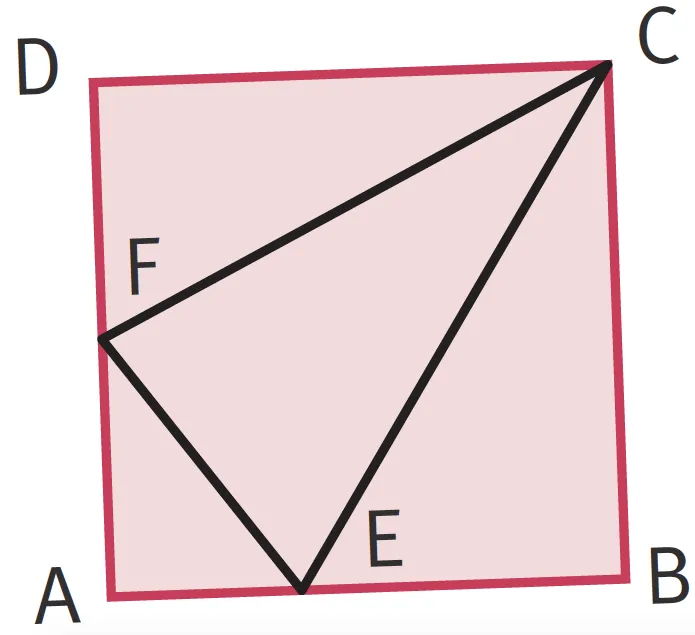Calculez l'aire du triangle $ECF$ .

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 1

On détermine la longueur des trois côtés du triangle, puis on démontre que le triangle est rectangle. On en calcule alors l'aire avec la formule du triangle rectangle.

Dans le triangle $AEF$ rectangle en $A$ , on applique le théorème de Pythagore :

EF^{2} = AE^{2} + AF^{2}

EF^{2} = 2, 5^{2} + 5^{2} = 6, 25 + 25 = 31, 25

EF = 31, 25

Dans le triangle $CDF$ rectangle en $D$ , on applique le théorème de Pythagore :

FC^{2} = DF^{2} + DC^{2}

FC^{2} = 5^{2} + 1 0^{2} = 25 + 100 = 125

FC = 125

Dans le triangle $EBC$ rectangle en $B$ , on applique le théorème de Pythagore :

EC^{2} = EB^{2} + BC^{2}

EC^{2} = 7, 5^{2} + 1 0^{2} = 56, 25 + 100 = 156, 25

EC = 156, 25

.

Le segment

[EF]

mesure

31, 25

cm

[FC]

125

cm

[EC] =

156, 25

cm

Dans le triangle $ECF$ , $[EC]$ est le plus grand côté et $EC2$ $= 156,25$ .

CF^{2} + FE^{2} = 125 + 31, 25 = 156, 25

On constate que

EC^{2} = CF^{2} + FE^{2}

.
D'après la réciproque du théorème de Pythagore, le triangle

ECF

est rectangle en

F

$A_{ECF} = FE \times FC \div 2 = 31, 25 \times 125 \div 2$

A_{ECF} = 31, 25

.

L'aire du triangle $ECF$ est égale à $31,25 cm$ $^{2}$ .

Corrigé 1

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 2

Pour calculer l'aire d'une forme géométrique inscrite dans une autre forme géométrique, on calcule l'aire totale de cette dernière puis on lui enlève l'aire des formes autres que celle dont on cherche l'aire.

$A_{ABCD} = 10 \times 10 = 100$
L'aire du carré $ABCD$ est égale à $100 cm$ ².
$AEF$ est rectangle en $A$ , $EBC$ en $B$ et $CDF$ en $D$ .

$AF = 10 \div 2 = 5$ $cm$
$A_{AEF} = 2, 5 \times 5 \div 2 = 6, 25$
Donc l'aire du triangle $AEF$ est égale à $6,25 c m^{2}$ .
$EB = 10 - 2, 5 = 7, 5$ $cm$
$A_{EBC} = 7, 5 \times 10 \div 2 = 37, 5$
L'aire du triangle $EBC$ est égale à $37,5 c m^{2}$ .
$DF = 10 \div 2 = 5$ $cm$
$A_{CDF} = 5 \times 10 \div 2 = 25$
L'aire du triangle $CDF$ est égale à $25 c m^{2}$ .

$A_{ECF} = 100 - (6, 25 + 37, 5 + 25) = 100 - 68, 75$
$A_{ECF} = 31, 25$

L'aire du triangle $ECF$ est égale à $31,25 cm$ ².

Corrigé 2

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

42
Problème similaire
Dans un trapèze

✔ Je structure mon raisonnement

Dans le trapèze

BCDE

suivant, les longueurs

BC = 6 cm

BE = 2,5 cm

Le zoom est accessible dans la version Premium.

Aire du trapèze :

A = (B + b) \times h \div 2

Coup de pouce

Calculez l'aire de ce trapèze.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Problèmes résolus

41
Un carré

42
Problème similaire
Dans un trapèze

Une erreur sur la page ? Une idée à proposer ?

Nous préparons votre pageNous vous offrons 5 essais

Les manuels scolaires

La communauté

Aide et utilisation

À propos

Problèmes résolus

41Un carré

42Problème similaireDans un trapèze

Une erreur sur la page ? Une idée à proposer ?

Nous préparons votre pageNous vous offrons 5 essais

Les manuels scolaires

La communauté

Aide et utilisation

À propos

41
Un carré

42
Problème similaire
Dans un trapèze