Exercices numériques

Nous allons chercher à donner des formules qui permettent de calculer des longueurs manquantes dans la figure suivante.Téléchargez le fichier ressource de l'exercice.

1. Rappeler les trois rapports de longueurs égaux selon le théorème de Thalès.

2. Ouvrez le document tableur de lʼexercice et, en suivant le modèle de la première case, remplissez les cases oranges avec les noms des longueurs pertinentes.

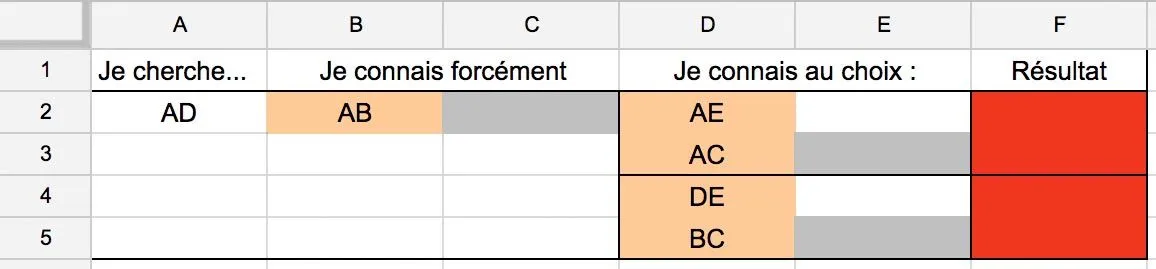3. En remplissant les cases grises avec les longueurs des côtés associés, on veut afficher dans la case rouge la valeur de la longueur recherchée. Remplissez le tableur avec les formules appropriées. On pourra tester les valeurs données en exemple ci-dessous.

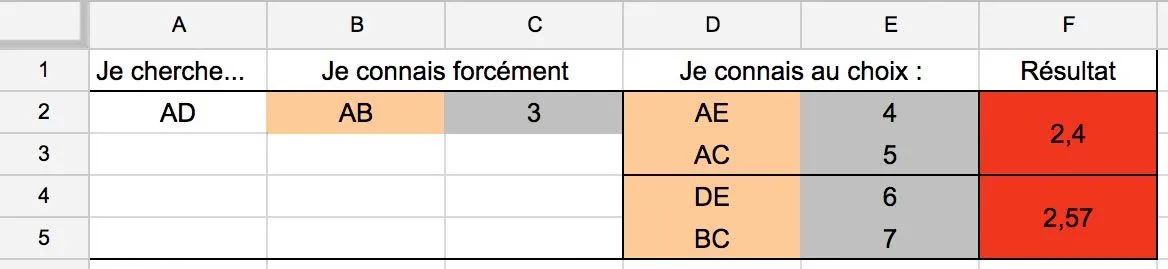4. À présent, ouvrez un logiciel de géométrie dynamique. Reproduisez la figure, et affichez les longueurs des différents côtés. Donnez à votre voisin les longueurs \mathrm{AB, AE} et \mathrm{AC}, et regardez s'il trouve la bonne valeur pour \mathrm{AD} avec le tableur. Vous pouvez ensuite recommencer en changeant la valeur des longueurs, et également les longueurs demandées.

Dans cet exercice, on se propose d'apprendre à utiliser conjointement le module d'algèbre et celui de géométrie pour vérifier le théorème de Thalès. Téléchargez le fichier ressource de l'exercice.


1. Reproduisez dans un logiciel de géométrie dynamique la figure de l'énoncé de lʼexercice n°48. On veut que la droite \mathrm{(DE)} soit parallèle à la droite \mathrm{(BC)}. Affichez ensuite les longueurs \mathrm{AD, AB, AE, AC, DE} et \mathrm{BC}.

2. Ouvrez une fenêtre de calcul, faites calculer au logiciel les rapports de grandeurs que l'on retrouve dans le théorème de Thalès.

3. Vous voyez s'afficher les valeurs de ces rapports de grandeurs. Que constatez-vous ? Faites varier la position des points \mathrm{A, B, C} et \mathrm{D}, un point à la fois. Que constatez-vous ?

Conservons toujours le triangle de lʼexercice n°48. Le programme que l'on se propose d'écrire permettra de déterminer si les droites \mathrm{(DE)} et \mathrm{(BC)} sont parallèles.

1. Quel égalité de rapports de longueurs doit-on tester pour appliquer la réciproque du théorème de Thalès ?

2. Savez-vous pourquoi, en informatique, lorsqu'on souhaite vérifier que deux rapports sont égaux, on préfère vérifier un produit en croix plutôt que de calculer une division ?

3. Ouvrez le document Scratch de l'exercice. On veut tester l'égalité des rapports de longueur \dfrac{a}{b} = \dfrac{c}{d} où a, b, c, d désignent les longueurs de la réponse à la première question. Complétez la condition pour que le programme fonctionne comme demandé.