Mathématiques 6e
Enseignant en primaire ?
Accompagnez-nous dans le développement d'une nouvelle collection !
Mes Pages
Du primaire au collège
Ch. 1
Manipuler les nombres entiers
Ch. 2
Les nombres décimaux
Ch. 3
Addition, soustraction
Ch. 4
Multiplication, division décimale
Ch. 5
Fractions
Ch. 6
Proportionnalité
Ch. 7
Construction de droites
Ch. 8
Distances et cercles
Ch. 9
Angles
Ch. 10
Symétrie axiale
Ch. 11
Triangles, rectangles et losanges
Ch. 12
Aire et périmètre
Ch. 13
Volumes
Chapitre 8
Pas à pas
2. Cercle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrir
a. Placer un point O sur le plan.
b. Placer quelques points situés à 3 cm de O.
c. Comment peut-on représenter tous les points à 3 cm de O ?
d. Où sont situés les points à une distance strictement inférieure à 3 cm de O ?
b. Placer quelques points situés à 3 cm de O.
c. Comment peut-on représenter tous les points à 3 cm de O ?
d. Où sont situés les points à une distance strictement inférieure à 3 cm de O ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
- Un cercle est la ligne sur laquelle se trouvent tous les points qui sont à une même distance d'un autre point, appelé le centre. Cette distance est le rayon.

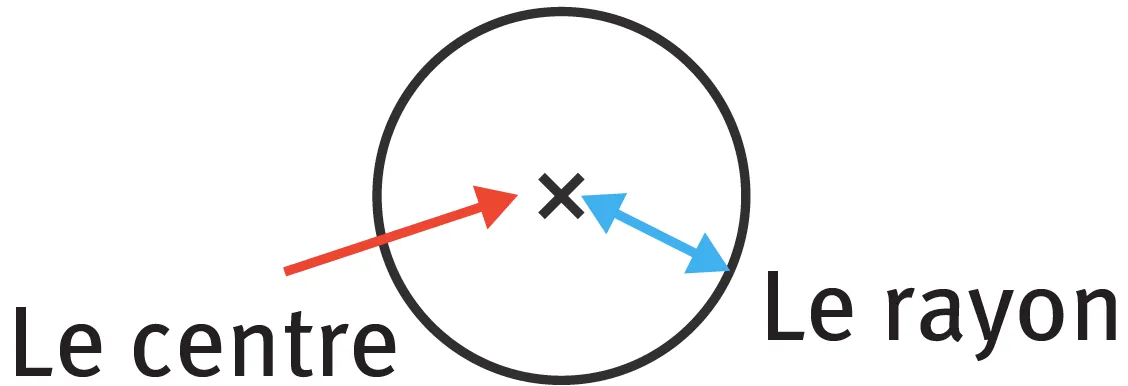
- Pour tracer un cercle, on utilise un compas, en fixant son ouverture sur le rayon du cercle.
- À chaque fois que l'on trace un cercle, on trace une infinité de points à égale distance du centre ! On ne peut pas tous les compter.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7 Tracer le cercle de centre B et de rayon AC

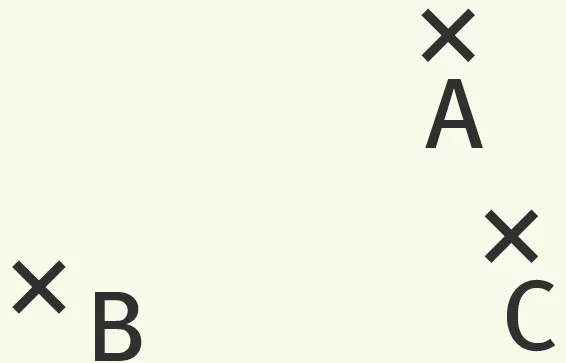
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
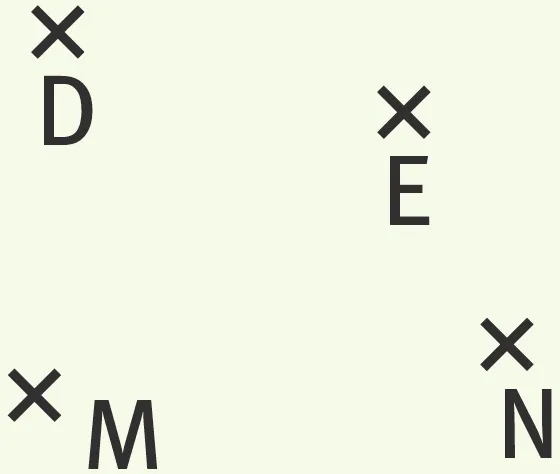
Exercice 8Tracer le cercle de centre D et de rayon MN

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retenir
- Vocabulaire :

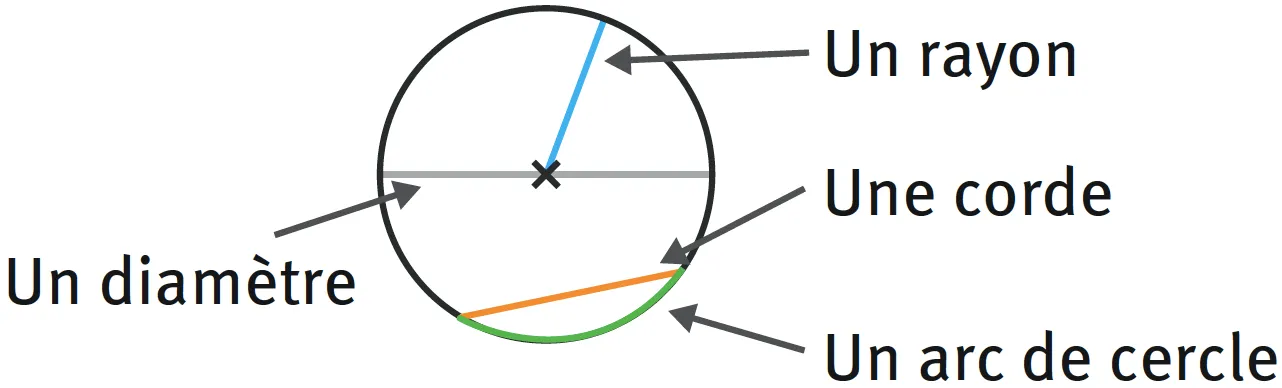
-
Remarques :
- Un rayon est un segment qui relie le centre du cercle à un point du cercle. Le rayon est la longueur d'un tel segment.
- Une corde est un segment reliant deux points d'un cercle.
- Un diamètre est une corde particulière qui passe par le centre du cercle.
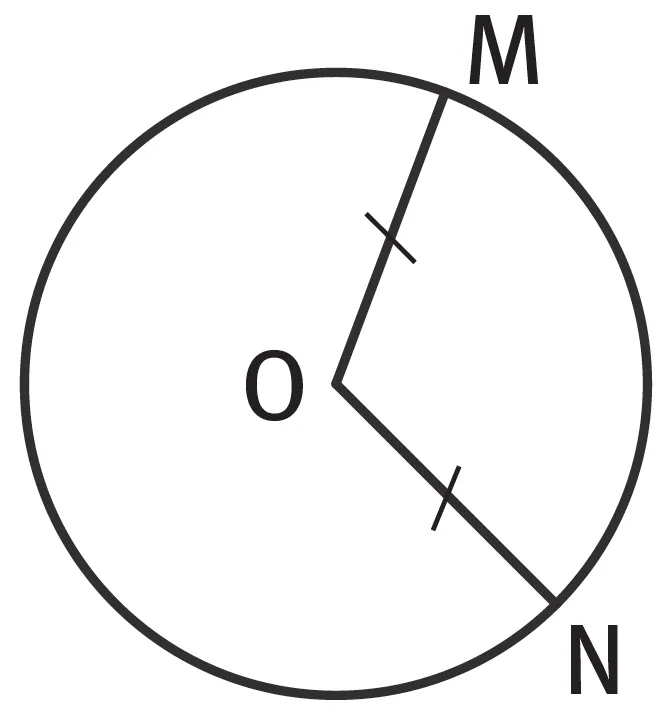
- Propriétés : Si deux points M et N appartiennent à un même cercle de centre O, alors OM = ON.
- Si OM = ON = r alors M et N sont sur le cercle de centre O et de rayon r.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Refaire Tracer un triangle dont les dimensions sont données
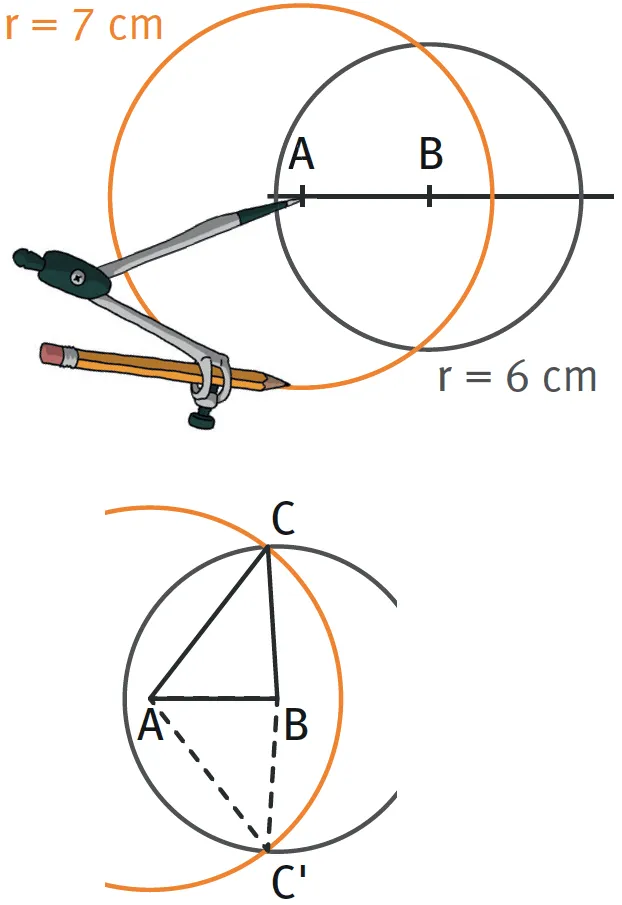
Tracer un triangle ABC tel que AB = 5 cm, BC = 6 cm et AC = 7 cm.
- On trace une droite. Sur cette droite, on place un point A.
- Avec la règle graduée, on place un point B sur la droite tel que AB = 5 cm.
- On ouvre le compas à 6 cm en s'aidant de la règle, et on trace un cercle de centre B.
- On ouvre le compas à 7 cm en s'aidant de la règle, et on trace un cercle de centre A.
- Le point C est sur chacun des cercles, donc sur leur intersection. On a le choix entre deux positions pour C : C et C'.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 9Construire un triangle ABC avec AB = 3 cm, AC = 4 cm et BC = 6 cm
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 10Construire un triangle TIC avec TI = 8 cm, IC = 5 cm et TC = 5 cm
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
