Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 13
Problèmes résolus
16 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32Triangles équilatéraux et semblables.
✔ Je reconnais une situation de proportionnalité
✔ Je représente des objets et des figures géométriques
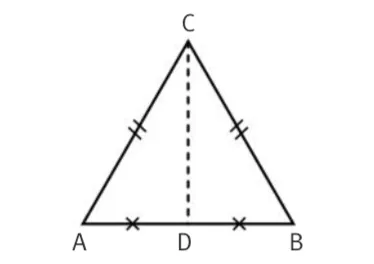
ABC est un triangle équilatéral. D est le milieu du segment [AB].
Démontrez que ADC et CDB sont semblables.
✔ Je représente des objets et des figures géométriques
ABC est un triangle équilatéral. D est le milieu du segment [AB].
Démontrez que ADC et CDB sont semblables.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Pour démontrer que deux triangles sont semblables, il est possible de montrer que les angles de ces triangles ont les mêmes mesures.
Corrigé 1
Le zoom est accessible dans la version Premium.
- ABC est équilatéral, donc tous ses angles mesurent 60^{\circ}. Donc C est équidistant de A et B. De plus, D est le milieu du segment [AB], il est donc lui aussi équidistant de A et B. Donc C et D appartiennent à la médiatrice de [AB].
- Or la médiatrice est perpendiculaire à [AB], donc les triangles ADC et CDB sont rectangles en D. Ces deux triangles ont donc un angle droit et un angle qui mesure 60^{\circ} (\widehat{\text{CAD}} pour le triangle CDA et \widehat{\text{CBD}} pour le triangle CDB).
- Donc pour ces deux triangles, le troisième angle mesure 180^{\circ} - 90^{\circ} - 60^{\circ} = 30^{\circ}. Les triangles CDB et ADC ont donc tous deux des angles valant 90^{\circ}, 60^{\circ} et 30^{\circ}, ils sont donc semblables.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Pour démontrer que deux triangles sont semblables, il est possible de montrer que la longueur des côtés de lʼun est proportionnelle à celle des côtés de lʼautre.
Corrigé 2
ABC est équilatéral et D est le milieu de [AB]. Donc AC = BC et AD = BD. Les deux triangles CDB et ADC ont un côté en commun : [DC].
Les deux triangles ont des côtés de longueurs égales deux à deux, ils sont donc égaux. Et puisque des triangles égaux sont aussi semblables, CDB et ADC sont des triangles semblables.
Les deux triangles ont des côtés de longueurs égales deux à deux, ils sont donc égaux. Et puisque des triangles égaux sont aussi semblables, CDB et ADC sont des triangles semblables.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33Problème similaireSymétrie centrale et triangles semblables.
✔ Je choisis un cadre adapté (numérique, algébrique ou géométrique) pour traiter un problème
ABC est un triangle rectangle isocèle en A. D est le symétrique de B par rapport à A.
Montrez que ACD et ABC sont semblables.
ABC est un triangle rectangle isocèle en A. D est le symétrique de B par rapport à A.
Montrez que ACD et ABC sont semblables.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah