Enseignement scientifique Terminale - 2024

Retourner à l'accueil
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Sciences, climat et société
Ouverture de thème
p. 12-14
Ch. 1
L’atmosphère terrestre et la vie
Ch. 2
La complexité du système climatique
Ch. 3
Le climat du futur
Se préparer à l'évaluation - Thème 1
Le futur des énergies
Ouverture de thème
p. 83
Ch. 4
Deux siècles d’énergie électrique
Ch. 5
Conversion et transport de l’énergie électrique
Ch. 6
Énergie, développement et futur climatique
Se préparer à l'évaluation - Thème 2
Une histoire du vivant
Une histoire du vivant
Ouverture de thème p. 152-154
Ch. 7
La biodiversité et son évolution
Ch. 8
L’évolution comme grille de lecture du monde
Ch. 9
L’évolution humaine
Ch. 10
Les modèles démographiques
Ch. 11
De l’informatique à l’intelligence artificielle
Se préparer à l'évaluation - Thème 3
Livret maths
Fiches méthode
Esprit critique et scientifique
Un panorama de la recherche scientifique
Fiche méthodep. 276
Différencier savoir, opinion et croyance
Fiche méthodep. 277
Apprécier la fiabilité d’une information sur Internet et savoir détecter les infox
Fiche méthodep. 278-279
Reconnaître et interpréter une relation de corrélation
Fiche méthodep. 280-281
Comprendre la construction des savoirs scientifiques
Fiche méthodep. 282
Identifier les différents biais cognitifs - Exclusivité numérique
Fiche méthode
Organiser un débat - Exclusivité numérique
Fiche méthode
Appréhender une controverse scientifique
Fiche méthode
Améliorer ses compétences
Fiches histoire
Annexes
Fiche méthode 4
Esprit critique et scientifique

Reconnaître et interpréter une relation de corrélation

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Relation, corrélation, causalité

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Relation

On peut mettre en relation deux grandeurs chiffrées, c'est-à-dire établir une relation mathématique entre elles, du moment qu'on dispose de plusieurs « mesures » chiffrées associant ces deux grandeurs. Pour visualiser cette relation, on trace généralement un graphique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exemples

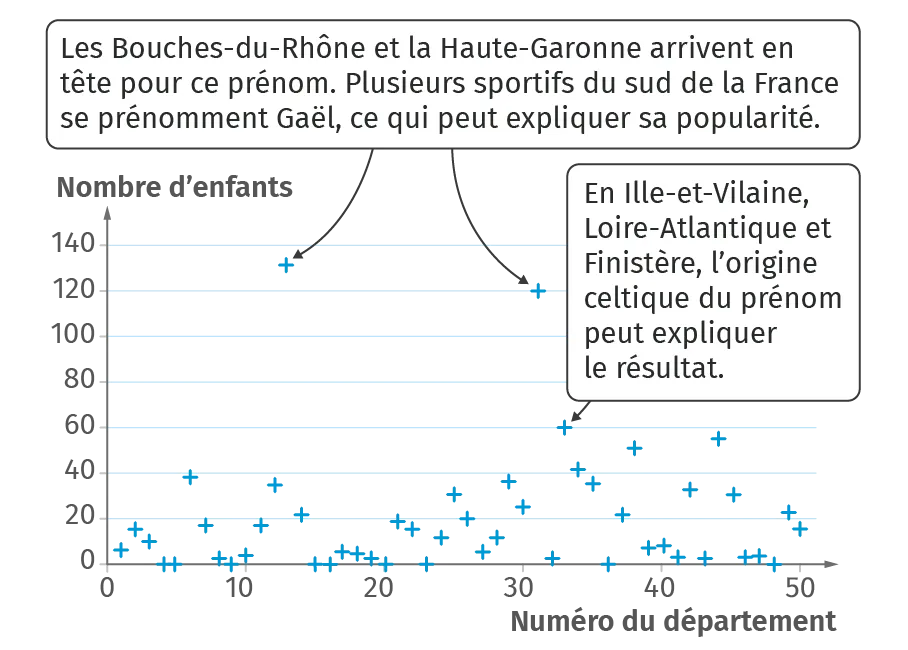
➜ Pour le graphique n°1, on peut établir une relation entre un nombre d'enfants prénommés Gaël et un numéro de département, car ce sont des données chiffrées (voir graphique n°1).

➜ En 2017, un chercheur tenta de montrer que les hommes considérés comme beaux ont davantage d'enfants de sexe féminin : une relation impossible à établir, car la beauté masculine n'est pas quantifiable par une mesure objective.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Placeholder pour relation entre le nombre d'enfants prénommés Gaël entre 2007 et 2017 et leur département de naissance relation entre le nombre d'enfants prénommés Gaël entre 2007 et 2017 et leur département de naissance
Graphique n°1 : relation entre le nombre d'enfants prénommés Gaël entre 2007 et 2017 et leur département de naissance
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Corrélation

Il y a corrélation de deux grandeurs chiffrées quand le tracé fait apparaître une relation mathématique, qui permet de prédire l'abscisse d'un point à partir de son ordonnée et vice-versa. Cette prédiction n'est pas exacte, elle constitue une estimation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exemples

➜ Pour le graphique n°1, il n'existe pas de corrélation entre le dépar- tement et le nombre d'enfants prénommés Gaël : on peut trouver des raisons pour lesquelles un département particulier a un tel résultat, mais il n'y a pas de régularité, une fonction mathématique ne permet pas de décrire l'ensemble.

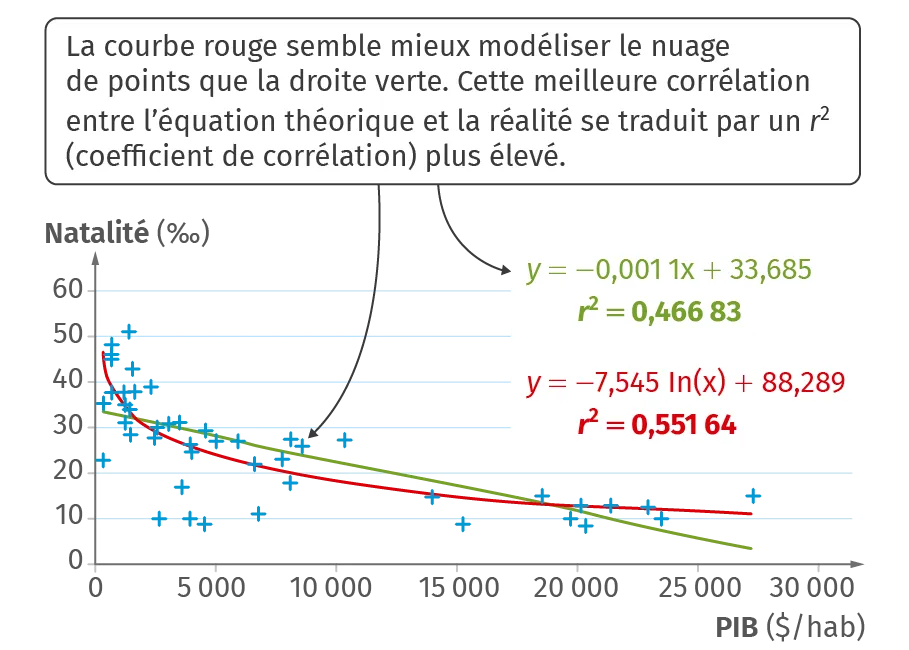
➜ Pour le graphique n°2, il semble y avoir une relation que l'on peut résumer ainsi : plus le PIB est élevé, plus la natalité est faible. Cette relation peut être formalisée par des équations de différents types.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Placeholder pour relation entre fécondité et PIB pour différents pays relation entre fécondité et PIB pour différents pays
Graphique n°2 : relation entre fécondité et PIB pour différents pays
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Causalité

Une corrélation ne signifie pas pour autant une causalité : ainsi, les deux grandeurs peuvent être proportionnelles tout en étant parfaitement indépendantes l'une de l'autre. Il y a causalité lorsqu'on peut montrer que la modification d'une grandeur entraîne la modification de l'autre dans un sens bien déterminé, pour une raison précise.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exemple

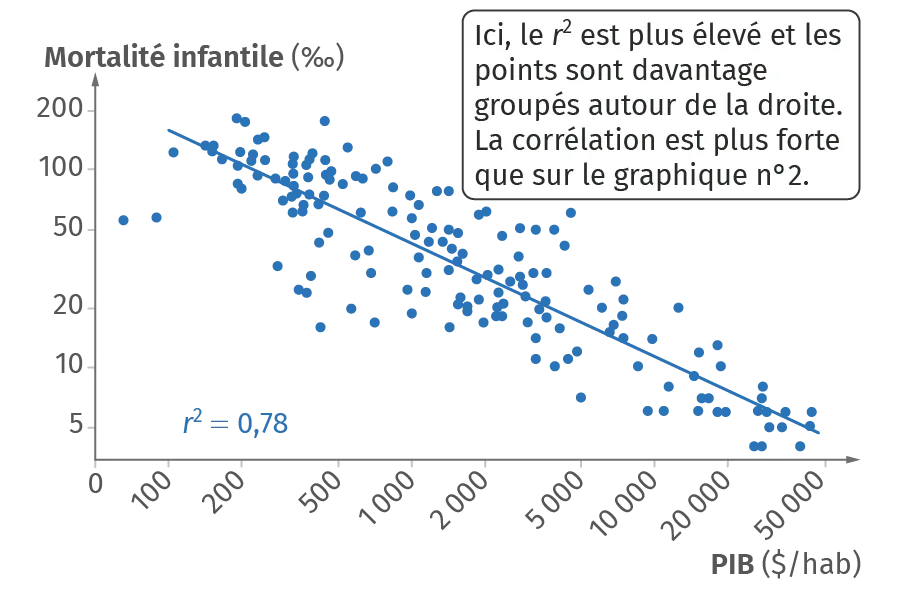
➜ Pour le graphique n°3, on peut établir une corrélation entre le PIB et la mortalité infantile, mais aussi une causalité, car les pays plus pauvres disposent en général de systèmes de santé moins efficaces.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Placeholder pour relation entre mortalité infantile et PIB relation entre mortalité infantile et PIB
Graphique n°3 : relation entre mortalité infantile et PIB
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Décrire et apprécier la solidité d'une corrélation

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Mise en évidence graphique de la corrélation

Pour avoir une idée de l'équation qui va représenter au mieux l'évolution observée, on essaie de tracer une courbe qui passe au plus près de tous les points. Par exemple, une droite traduit mathématiquement une relation de proportionnalité.
Sur un tableur, on peut tracer cette droite, appelée courbe de régression ou courbe de tendance. Ce peut être aussi une autre fonction mathématique (exponentielle, logarithmique, etc.).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Le coefficient de corrélation

La solidité de la corrélation, c'est-à-dire la probabilité de tomber juste en utilisant l'équation de la droite, est donnée par le coefficient de corrélation r2. C'est une mesure de l'écart moyen des points à la droite. Plus ce coefficient est proche de 1 (100 %), meilleure est la corrélation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exemples

➜ Pour le graphique n°2, les points sont plutôt éloignés de la droite ; le coefficient r2 est de 0,46 (46 %), ce qui est faible. La corrélation n'est pas parfaite : cela témoigne de la complexité de la relation. Le PIB est un paramètre explicatif de la natalité, mais il n'en est pas le seul. Une fonction de type logarithmique, plus complexe, semble un peu mieux adaptée : le coefficient est alors de 0,55.

➜ Pour le graphique n°3, la corrélation est plus solide (r2 = 0,78) : le taux de mortalité infantile dépend très fortement du PIB.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

C
Corrélation n'est pas causalité

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Détecter les corrélations non informatives

Dire qu'une grandeur est proportionnelle à une autre ne signifie pas pour autant que la variation de l'une est la cause directe de la variation de l'autre. Il peut en effet s'agir d'une coïncidence, ou encore d'un effet plus subtil : la présence d'une variable explicative commune (variable de confusion).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Placeholder pour relation entre production de glaces aux États-Unis et morts par noyade dans des piscinesrelation entre production de glaces aux États-Unis et morts par noyade dans des piscines
Graphique n°4 : relation entre production de glaces aux États-Unis et morts par noyade dans des piscines.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exemple

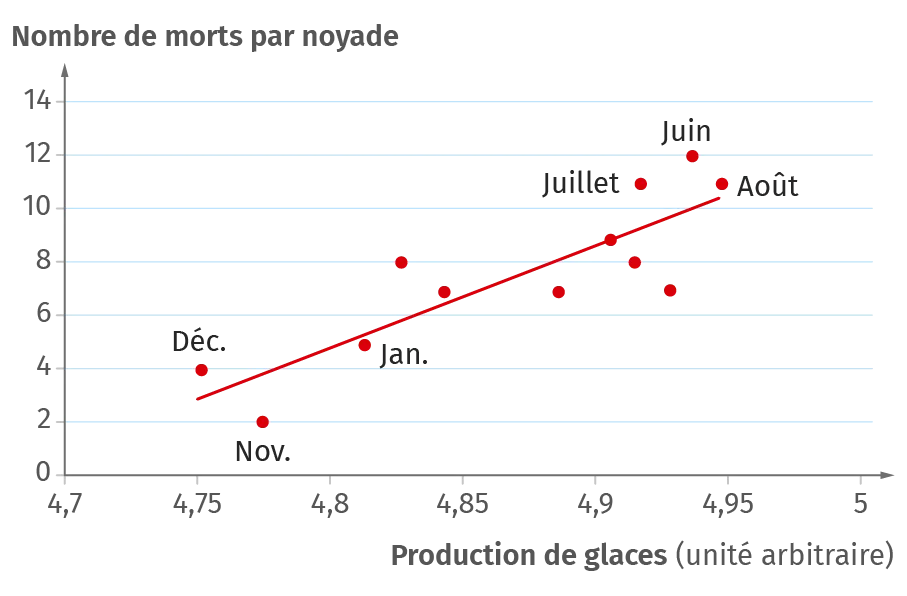
➜ Dans le graphique n°4, il y a une corrélation entre la vente de glaces aux États-Unis et le nombre de morts par noyade. Manger de la glace peut-il augmenter le risque de se noyer ? En réalité, il y a ici une variable de confusion qui est la température : plus il fait chaud, plus on vend de glaces, mais plus il y a également de baigneurs, donc de noyades.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Argumenter une relation de causalité

La causalité ne se démontre pas mathématiquement : une fois que l'on a obtenu une corrélation, il faut construire un raisonnement plausible pouvant expliquer que l'une des variables varie en fonction de l'autre. Attention à ne pas confondre la cause et la conséquence !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exemple

➜ Pour le graphique n°3, on peut argumenter que les pays disposant d'un PIB et donc de ressources élevées mettent en place des politiques de santé et d'éducation, ce qui a pour conséquence d'éviter une grande partie des décès de nourrissons. À l'inverse, la mortalité infantile faible n'est probablement pas la cause d'un PIB élevé. On pourrait aussi suggérer que les pays au PIB élevé ont les moyens de défendre leur espace aérien contre les extraterrestres, qui sont responsables du décès des enfants en bas âge : ce scénario correspond aux données, mais il est peu probable...
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Ainsi, la présence d'une corrélation n'est pas une démonstration de causalité, mais seulement un argument en sa faveur, s'il est étayé par un raisonnement, qui n'est pas irréfutable, mais plus ou moins plausible.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Supplément numérique

Découvrez des
corrélations absurdes
.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.