Physique-Chimie 3e - Cahier d'activités - 2023

Nouveau manuel de Sciences et Technologie 6e
Découvrez cet ouvrage collaboratif, conforme au nouveau programme !
Mes Pages
Thème 1 : Organisation et transformations de la matière
Ch. 1
Les espèces chimiques et l'identification
Ch. 2
Les transformations chimiques
Ch. 3
Les états de la matière
Ch. 4
Les mélanges et la solubilité
Ch. 5
L'organisation de la matière dans l'Univers
Thème : 2 Mouvements et interactions
Ch. 6
La vitesse des systèmes
Ch. 7
Les nature des mouvements
Ch. 8
La modélisation des actions
Thème 3 : Énergie, transferts et conversions
Ch. 9
Les différentes formes d’énergie et les conversions
Ch. 10
Les circuits électriques et les lois
Ch. 11
La puissance électrique et la consommation
Thème 4 : Signaux pour observer et communiquer
Ch. 12
Les signaux lumineux et sonores
Annexes
Fiches méthodes
6 - La vitesse des systèmes
Activité documentaire
Changement climatique
La surveillance du climat
✔ Caractériser la vitesse par sa direction, son sens et sa valeur.
✔ Relier la distance parcourue par la lumière à la durée de sa propagation.
✔ Relier la distance parcourue par la lumière à la durée de sa propagation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Introduction
Les satellites européens Météosat sont conçus pour transmettre des images numériques de la Terre. Ces images permettent aux météorologues de prévoir les conditions météorologiques et certains phénomènes tels que les ouragans et les tempêtes, et de suivre les changements climatiques à l'échelle de la planète. Les satellites Météosat jouent donc un rôle crucial dans la protection de la population en fournissant des informations précises et fiables sur les conditions météorologiques et climatiques en temps réel.
Problématique
Comment évolue la vitesse de ces satellites au cours de leur mouvement de rotation ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
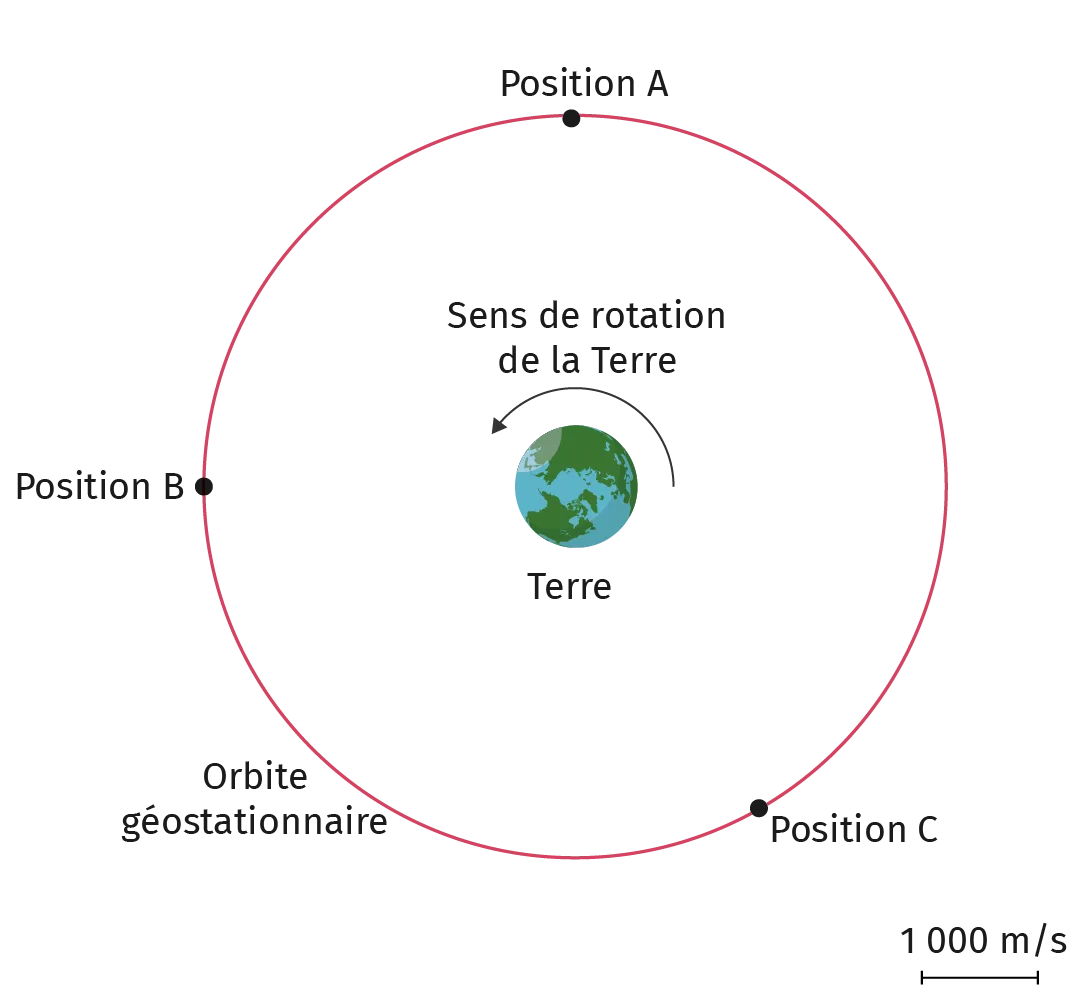
Doc. 1Orbite des satellites Météosat
Les satellites Météosat sont géostationnaires car ils sont placés sur une orbite particulière autour de la Terre qui leur permet de rester à la même position par rapport à la surface de la planète.
Cette orbite géostationnaire se situe à 36 000 km au-dessus de la Terre. Elle est choisie pour que le satellite tourne autour de la Terre à la même vitesse que celle-ci. Cela signifie que, même si la Terre tourne sur elle-même, le satellite reste en place au-dessus d'un point donné à la surface de la planète.
Grâce à cette orbite, les satellites Météosat peuvent fournir une couverture constante de la météo et du climat sur une grande partie de la surface de la Terre.
Cette orbite géostationnaire se situe à 36 000 km au-dessus de la Terre. Elle est choisie pour que le satellite tourne autour de la Terre à la même vitesse que celle-ci. Cela signifie que, même si la Terre tourne sur elle-même, le satellite reste en place au-dessus d'un point donné à la surface de la planète.
Grâce à cette orbite, les satellites Météosat peuvent fournir une couverture constante de la météo et du climat sur une grande partie de la surface de la Terre.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'orbite géostationnaire est très occupée par les satellites artificiels : on en dénombre près de 560 !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Vitesse de propagation de la lumière : c=300 000 000 \mathrm{~m} / \mathrm{s}
Rayon de la Terre : \mathrm{R_T = 6 370 km}
Périmètre d'un cercle de rayon \bf{r} : p=2 \times \pi \times r
Rayon de la Terre : \mathrm{R_T = 6 370 km}
Périmètre d'un cercle de rayon \bf{r} : p=2 \times \pi \times r
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Vitesse
Les données collectées par les satellites géostationnaires sont envoyées sous forme de signaux électromagnétiques vers la Terre. Ces signaux se déplacent à la vitesse de propagation de la lumière c.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3Direction et sens de la vitesse
La direction et le sens sont des caractéristiques de la vitesse, au même titre que la valeur que l'on exprime en mètre par seconde (\mathrm{m/s}) ou en kilomètre par heure (\mathrm{km/h}). La direction est une droite tandis que le sens est une orientation (vers le haut ou vers le bas par exemple).


Pour un mouvement rectiligne, la direction se confond avec la trajectoire du mouvement.


En revanche, pour tous les autres mouvements de trajectoires plus complexes (comme les mouvements circulaires), la direction ne correspond pas à la trajectoire suivie sur tout le mouvement, mais uniquement au cours d'un bref instant. Elle correspondrait à la trajectoire de l'objet si toutes les actions ressenties par l'objet disparaissaient d'un seul coup !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
1. Les signaux envoyés par les satellites géostationnaires Météosat mettent un certain temps à arriver sur Terre. Calculer la durée de propagation de ces signaux en utilisant les informations des Doc. 1 et Doc. 2.
2. Sachant que la trajectoire correspond à un cercle, calculer la distance d parcourue en une journée par un satellite.
3. Les satellites géostationnaires de Météosat effectuent leur mouvement de rotation autour de la Terre avec une valeur de vitesse constante : on parle de mouvement uniforme. En déduire la valeur de la vitesse v de ces satellites.
4. Sur le schéma ci-dessous, représenter par des pointillés les directions de la vitesse au niveau des points \mathrm{A}, \mathrm{B} et \mathrm{C}.
5. La Terre tourne dans le sens inverse des aiguilles d'une montre lorsqu'on l'observe au-dessus du pôle Nord. Préciser alors les sens des vitesses représentées aux points \mathrm{A}, \mathrm{B} et \mathrm{C}.
6. En utilisant l'échelle fournie, tracer les vitesses aux points \mathrm{A}, \mathrm{B} et \mathrm{C} en tenant compte de leur valeur, de leur direction et de leur sens.
7. Choisir les bonnes réponses pour répondre à la problématique.
Cliquer ici pour avoir accès au schéma
5. La Terre tourne dans le sens inverse des aiguilles d'une montre lorsqu'on l'observe au-dessus du pôle Nord. Préciser alors les sens des vitesses représentées aux points \mathrm{A}, \mathrm{B} et \mathrm{C}.
Cliquer ici pour avoir accès au schéma
7. Choisir les bonnes réponses pour répondre à la problématique.
Au cours de leur mouvement, les satellites Météosat décrivent une trajectoire avec une vitesse dont la est constante. En revanche, à chaque instant, la ainsi que le sens évoluent. Les caractéristiques de la vitesse les mêmes en tout point de la trajectoire.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
