Mathématiques 1re Techno
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 3
Avant de commencer
Dérivation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Interpréter graphiquement le nombre dérivé comme coefficient directeur de la tangente.
2. Construire la tangente à une courbe en un point.
3. Déterminer l'équation réduite de la tangente à une courbe en un point.
4. Calculer la dérivée d'une fonction polynôme de degré inférieur ou égal à trois.
5. Déterminer le sens de variation et les extremums d'une fonction polynôme de degré inférieur ou égal à 3.
2. Construire la tangente à une courbe en un point.
3. Déterminer l'équation réduite de la tangente à une courbe en un point.
4. Calculer la dérivée d'une fonction polynôme de degré inférieur ou égal à trois.
5. Déterminer le sens de variation et les extremums d'une fonction polynôme de degré inférieur ou égal à 3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Construit en 1749, le « pont mathématique » de l'université de Cambridge (Angleterre) est un pont dont la structure est composée de poutres tangentes à la forme du pont.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rappels théoriques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étudier une fonction affine :
Définition :
Une fonction affine est une fonction de la forme f : x \mapsto ax + b, avec a et b deux réels.Propriété :
Une fonction affine est représentée par une droite dans un repère.Propriété :
Une fonction affine est strictement croissante si a\gt0, strictement décroissante si a\lt0.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dresser un tableau de variations :
Définition :
Un tableau de variations permet de résumer le sens de variation d'une fonction f selon les valeurs de x. La fonction est représentée par une flèche montante lorsqu'elle est croissante, et descendante lorsqu'elle est décroissante.Le tableau peut se construire à partir du graphique de la fonction ou par le calcul.
Méthode :
Soit f la fonction représentée ci‑dessous.
1. On commence par déterminer son ensemble de définition, ici \left[ -1 ; + \infty \right].
2. On note les points où la fonction change de sens de variations : ici, en -0,5 et 0{,}5.
3. On dresse le tableau.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer une équation de droite dans un repère :
Définition :
Une droite non verticale du plan est représentée par une équation de droite de la forme y = ax+b. Le coefficient a est appelé pente ou coefficient directeur de la droite, et le coefficient b est appelé ordonnée à l'origine.Une droite verticale est représentée par une équation du type x = a.
Méthode :
Graphiquement,1. Pour déterminer l'ordonnée à l'origine, il suffit de relever l'ordonnée du point d'intersection entre la droite et l'axe des ordonnées ;
2. Pour déterminer le coefficient directeur, on choisit deux points distincts de la droite \text{A}(x_\text{A} \: ; \: y_\text{A}) et \text{B}(x_\text{B} \: ; \: y_\text{B}). Le coefficient directeur est alors donné par a = \dfrac{y_\text{B} - y_\text{A}}{x_\text{B} - x_\text{A}}.
Exemple :
La droite ci‑dessous coupe l'axe des ordonnées au point \text{A}(0 \: ; 2). Son ordonnée à l'origine est donc 2.Les points \text{A}(0 \: ; 2) et \text{B}(3\: ; 6) sont sur la droite. Le coefficient directeur est donc a = \dfrac{y_\text{B} - y_\text{A}}{x_\text{B} - x_\text{A}} = \dfrac{6-2}{3-0} = \dfrac{4}{3}.
Une équation de la droite est donc y = \dfrac{4}{3}x + 2.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Construire un tableau de signe :
Définition :
Le tableau de signe permet de résumer le signe d'une expression dépendant de x en fonction des valeurs prises par x.Pour le construire, on factorise au maximum l'expression, on étudie le signe de chacun des facteurs, puis on utilise la règle des signes.
Exemple :
On veut étudier le signe de (x+1)(2x +6) pour x un nombre réel.On résout les inéquations x+ 1 \leqslant 0 \Leftrightarrow x \leqslant -1 et 2x + 6 \leqslant 0 \Leftrightarrow 2x \leqslant -6 \Leftrightarrow x \leqslant \dfrac{-6}{2} = -3.
Enfin, on dresse le tableau de signe donnant le signe de chacun des facteurs en fonction de la valeur de x, et on déduit le signe du produit en utilisant la règle des signes.

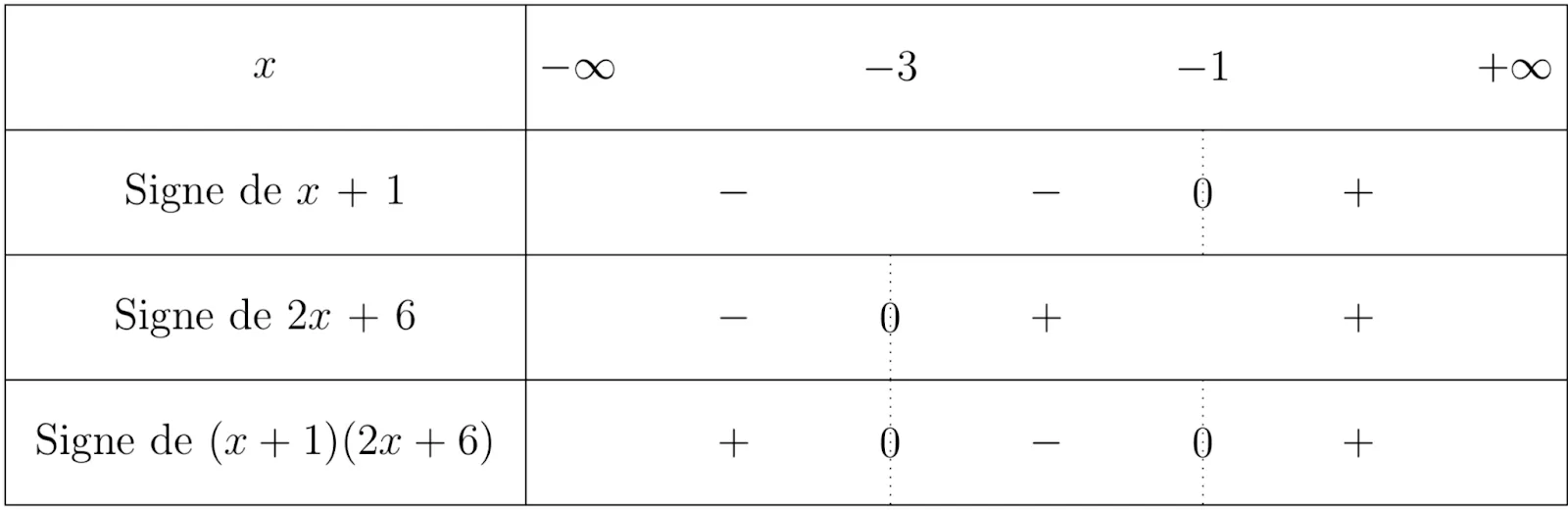
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Étudier une fonction affine.
2. Déterminer une équation de droite dans un repère.
3. Dresser un tableau de variations.
4. Construire un tableau de signe.
2. Déterminer une équation de droite dans un repère.
3. Dresser un tableau de variations.
4. Construire un tableau de signe.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1Déterminer une équation de droite
Déterminer les équations réduites des droites tracées dans le repère ci‑dessous.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2Coefficients d'une fonction affine
Chacune des fonctions affines ci‑dessous peut s'écrire sous la forme mx + p. Déterminer, dans chaque cas, la valeur de m et de p.
1. f(x)=3-x
2. g(x)=-x+1
3. h(x)=-4
4. k(x)=\frac{2 x-1}{3}
1. f(x)=3-x
2. g(x)=-x+1
3. h(x)=-4
4. k(x)=\frac{2 x-1}{3}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3Appartenance à une droite
On considère, dans un repère orthonormé (\mathrm{O} \: ; \mathrm{I} \:, \mathrm{J}), la droite d d'équation y = -3x + 1. Parmi les quatre points suivants, quels sont ceux appartenant à d ?
1. \mathrm{A}(0 \: ; 1)
2. \mathrm{B}(-3 \: ;-10)
3. \mathrm{C}(1 \: ;-2)
4. \mathrm{D}\left(-\frac{2}{3} \: ;-3\right)
1. \mathrm{A}(0 \: ; 1)
2. \mathrm{B}(-3 \: ;-10)
3. \mathrm{C}(1 \: ;-2)
4. \mathrm{D}\left(-\frac{2}{3} \: ;-3\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4Construire un tablau de signe
Grâce à notre outil d'édition d'image, compléter le tableau de signe de la fonction f définie sur [-5 \: ; 5] par : f(x)=(x+3)(-2 x+3).


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5Problème
On considère les fonctions f et g définies sur [-3 \: ; 5] par f(x)=x+1 et g(x)=-0,5 x^{2}+x+3. On a représenté ci‑dessous leur courbe représentative dans un repère orthonormé.

1. Par lecture graphique, construire les tableaux de variations des fonctions f et g sur [-3 \: ; 5].
2. Justifier les variations de f.
3. Résoudre graphiquement l'équation f(x)=g(x), puis vérifier algébriquement le résultat obtenu.

1. Par lecture graphique, construire les tableaux de variations des fonctions f et g sur [-3 \: ; 5].
Cliquez pour accéder à une zone de dessin
2. Justifier les variations de f.
3. Résoudre graphiquement l'équation f(x)=g(x), puis vérifier algébriquement le résultat obtenu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Au cours du XVIIe siècle, une polémique enflamma le monde des mathématiques pour savoir qui, d'Isaac Newton ou de Gottfried Wilhelm Leibniz, était le père du calcul infinitésimal (calcul sur des nombres infiniment petits). Quand Newton parlait de « fluxion » et avait une approche numérique du phénomène, Leibniz en avait plutôt développé une approche géométrique. Cette polémique était probablement surtout une question de prestige national entre l'Angleterre et l'Allemagne. Si elle fait encore débat aujourd'hui, on s'accorde au moins sur le fait qu'aucun des deux n'a plagié l'autre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
