Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 3
Exercices
Préparer le bac
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice corrigé[D'après EC sujet T1CMATH03525.]
La courbe \mathcal{C}_f ci‑dessous est la représentation graphique, dans un repère orthonormé, d'une fonction f définie et dérivable sur l'intervalle [-6 \: ; 14].
La droite \mathrm{T}_{\mathrm{A}} est la tangente à la courbe \mathcal{C}_f au point \text{A}.
La droite \mathrm{T}_{\mathrm{B}} est la tangente à la courbe \mathcal{C}_f au point \text{B}.
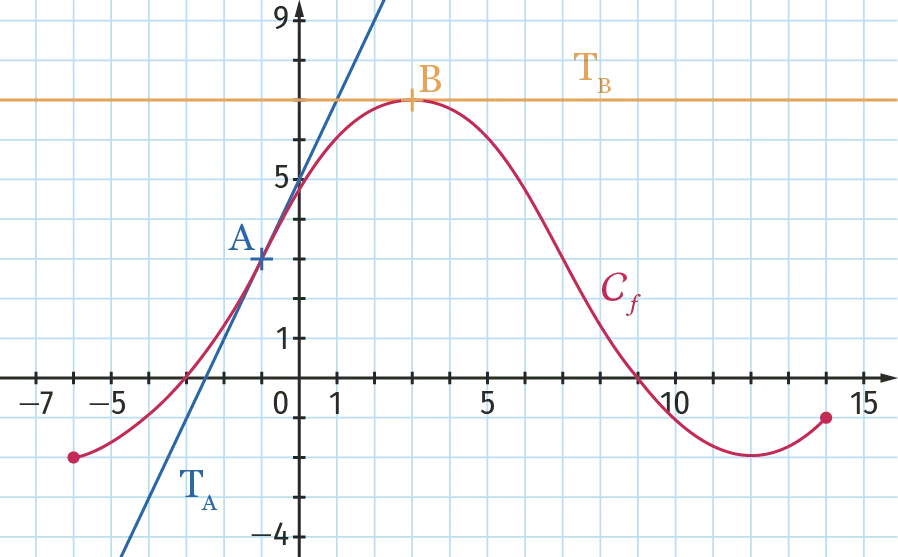
Utiliser le graphique pour répondre aux questions suivantes.
1. Déterminer f(3) et f^{\prime}(3).
2. Déterminer f(-1) et f^{\prime}(-1).
3. Résoudre graphiquement l'équation f(x)=6.
4. Dresser le tableau de variations de la fonction f sur l'intervalle [-6 \: ; 14] en y faisant figurer le signe de f^{\prime}(x).
5.
Une seule des trois courbes suivantes peut être la représentation graphique de f^{\prime}, la fonction dérivée de la fonction f. Laquelle ? Justifier.
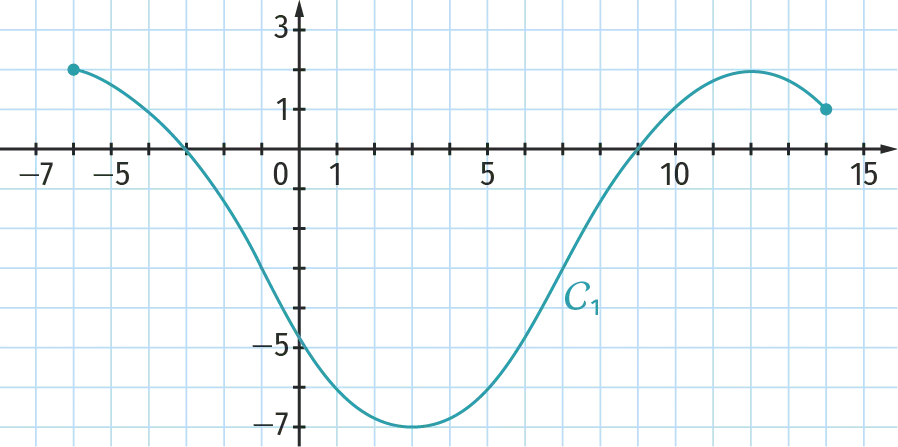
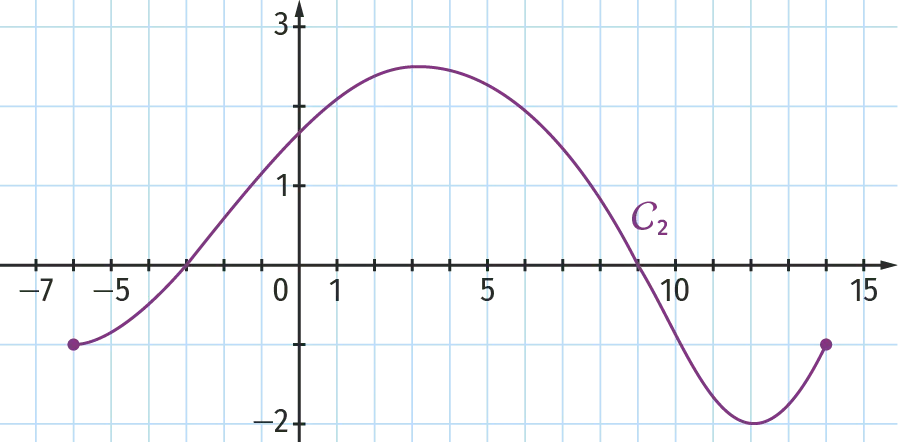
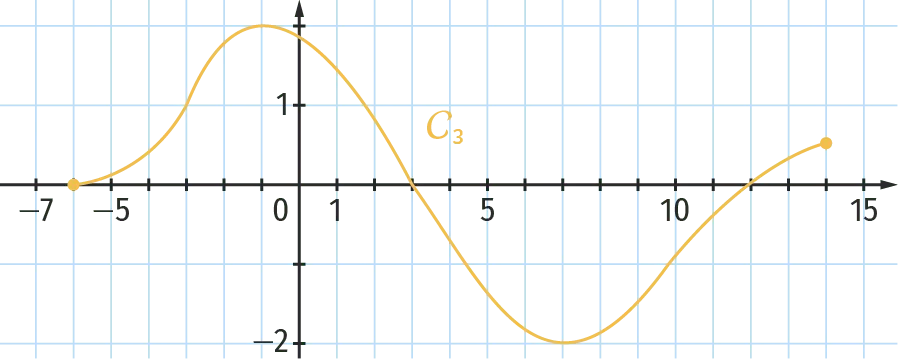
La droite \mathrm{T}_{\mathrm{A}} est la tangente à la courbe \mathcal{C}_f au point \text{A}.
La droite \mathrm{T}_{\mathrm{B}} est la tangente à la courbe \mathcal{C}_f au point \text{B}.
Le zoom est accessible dans la version Premium.
Utiliser le graphique pour répondre aux questions suivantes.
1. Déterminer f(3) et f^{\prime}(3).
2. Déterminer f(-1) et f^{\prime}(-1).
3. Résoudre graphiquement l'équation f(x)=6.
4. Dresser le tableau de variations de la fonction f sur l'intervalle [-6 \: ; 14] en y faisant figurer le signe de f^{\prime}(x).
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution rédigée
1. f(3) est l'ordonnée du point \text{B} donc f(3)=7.
f^{\prime}(3) est le coefficient directeur de la tangente à la courbe au point \text{B}. Donc f^{\prime}(3)=0.
2. f(-1) est l'ordonnée du point \text{A} donc f(-1)=3.
f^{\prime}(-1) est le coefficient directeur de la tangente à la courbe au point \text{A}.
D'après le graphique, \mathrm{T}_{\mathrm{A}} passe par les points \mathrm{A}(-1 \: ; 3) et \mathrm{C}(0 \: ; 5). Donc f^{\prime}(-1)=\frac{y_{\mathrm{C}}-y_{\mathrm{A}}}{x_{\mathrm{C}}-x_{\mathrm{A}}}=\frac{5-3}{0-(-1)}=2.
3. Les solutions de l'équation f(x)=6 sont les abscisses des points de la courbe dont l'ordonnée vaut 6. Donc \mathrm{S}=\{1 ; 5\}.
4. Les variations de f donnent le signe de f^{\prime}.
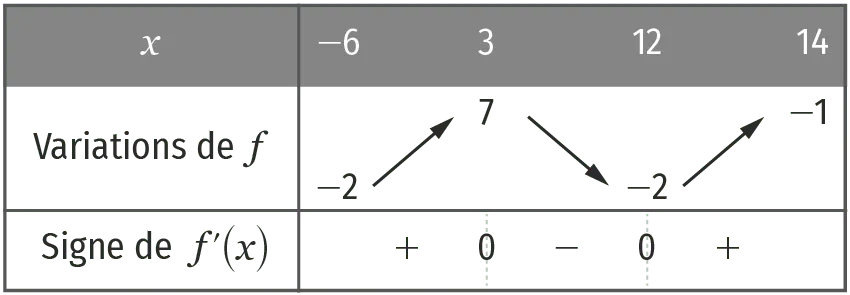
5. La seule courbe représentant une fonction positive sur l'intervalle [-6 \: ; 3] est la courbe \mathcal{C}_3, c'est donc la courbe représentative de la fonction f^{\prime}.
f^{\prime}(3) est le coefficient directeur de la tangente à la courbe au point \text{B}. Donc f^{\prime}(3)=0.
2. f(-1) est l'ordonnée du point \text{A} donc f(-1)=3.
f^{\prime}(-1) est le coefficient directeur de la tangente à la courbe au point \text{A}.
D'après le graphique, \mathrm{T}_{\mathrm{A}} passe par les points \mathrm{A}(-1 \: ; 3) et \mathrm{C}(0 \: ; 5). Donc f^{\prime}(-1)=\frac{y_{\mathrm{C}}-y_{\mathrm{A}}}{x_{\mathrm{C}}-x_{\mathrm{A}}}=\frac{5-3}{0-(-1)}=2.
3. Les solutions de l'équation f(x)=6 sont les abscisses des points de la courbe dont l'ordonnée vaut 6. Donc \mathrm{S}=\{1 ; 5\}.
4. Les variations de f donnent le signe de f^{\prime}.
Le zoom est accessible dans la version Premium.
5. La seule courbe représentant une fonction positive sur l'intervalle [-6 \: ; 3] est la courbe \mathcal{C}_3, c'est donc la courbe représentative de la fonction f^{\prime}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 99
[D'après EC sujet T1CMATH03531.]
Le chiffre d'affaires, en milliers d'euros, d'une entreprise en fonction du temps est modélisé par la fonction f(x)=3 x\left(48 x-5 x^{2}\right), où x représente le nombre d'années.
1. a. Pour tout x \gt 0, développer f(x).
b. En déduire l'expression de f^{\prime}.
c. On admet que f^{\prime}(x)=-3 x(15 x-96).
Dresser le tableau de variation de f.
d. En déduire le maximum de f sur [0 \: ; 10].
Interpréter ce résultat dans le cadre de l'exercice.
2. Compléter la ligne 9 du programme écrit en Python ci‑dessous afin qu'en fin d'exécution, la variable \color{purple}\bf{M} contienne une valeur approchée du chiffre d'affaires maximal, exprimé en millier d'euros.
1. a. Pour tout x \gt 0, développer f(x).
b. En déduire l'expression de f^{\prime}.
c. On admet que f^{\prime}(x)=-3 x(15 x-96).
Dresser le tableau de variation de f.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
d. En déduire le maximum de f sur [0 \: ; 10].
Interpréter ce résultat dans le cadre de l'exercice.
2. Compléter la ligne 9 du programme écrit en Python ci‑dessous afin qu'en fin d'exécution, la variable \color{purple}\bf{M} contienne une valeur approchée du chiffre d'affaires maximal, exprimé en millier d'euros.
def chiffresaffairesmax():
x = 0
B = 3*x*(48*x - 5*x**2)
M = B
for k in range(100):
x = x + 0.1
B = 3*x*(48*x - 5*x**2)
if B > M :
M = ...
return M
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 100
[D'après EC sujet T1CMATH03528.]
Le zoom est accessible dans la version Premium.
Une entreprise produit et vend des courgettes. Elle a la capacité d'en produire entre 0 et 16 tonnes.
On note \mathrm{C}(x) le coût de production, exprimé en euros, de x tonnes de courgettes.
La fonction \mathrm{C} est donc définie sur [0 \: ; 16] et elle est donnée par \mathrm{C}(x)=x^{3}-15 x^{2}+78 x-650.
Chaque tonne de courgettes est vendue 150 €.
On rappelle que le bénéfice correspond à la différence entre la recette et le coût de production.
1. Vérifier que le bénéfice \mathrm{B}(x) s'exprime, pour tout x \in[0 \: ; 16], par \mathrm{B}(x)=-x^{3}+15 x^{2}+72 x+650.
2. On admet que la fonction \text{B} est dérivable sur [0 \: ; 16] et on note \text{B}^{\prime} sa fonction dérivée. Déterminer \text{B}^{\prime}(x).
3. Montrer que \mathrm{B}^{\prime}(x)=-3(x+2)(x-12) pour x dans l'intervalle [0 \: ; 16].
4. À l'aide d'un tableau de signe, étudier le signe de \mathrm{B}^{\prime}(x) sur l'intervalle [0 \: ; 16], puis en déduire le tableau de variations de la fonction \text{B} sur [0 \: ; 16].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
5. Quelle quantité de courgettes l'entreprise doit‑elle produire et vendre pour avoir un bénéfice maximal ?
Quel est alors ce bénéfice ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 101
[D'après EC sujet T1CMATH03526.]
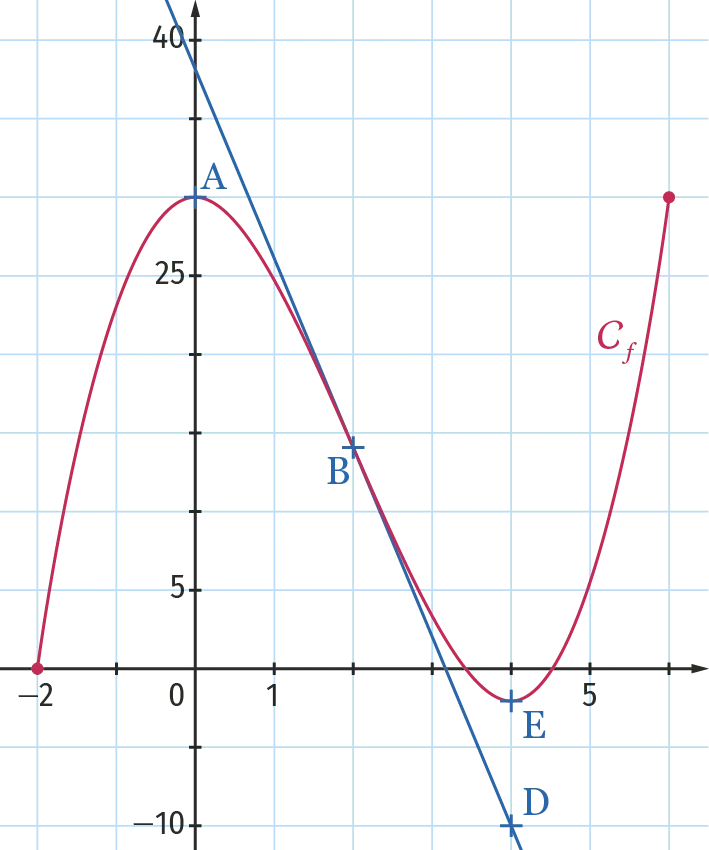
Soit f la fonction définie sur l'intervalle [-2 \: ; 6] dont la courbe représentative \mathcal{C}_f est donnée ci‑dessous.
On note f^{\prime} la fonction dérivée de la fonction f sur l'intervalle [-2 \: ; 6].
On considère les points \mathrm{A}(0 \: ; 30), \mathrm{B}(2 \: ; 14), \mathrm{D}(4 \: ; -10) et \mathrm{E}(4 \: ; -2). \text{A}, \text{B} et \text{E} sont trois points de la courbe \mathcal{C}_f.
La droite (\text{BD}) est la tangente à la courbe \mathcal{C}_f au point \text{B}.
Les tangentes à la courbe \mathcal{C}_f aux points \text{A} et \text{E} sont parallèles à l'axe des abscisses.
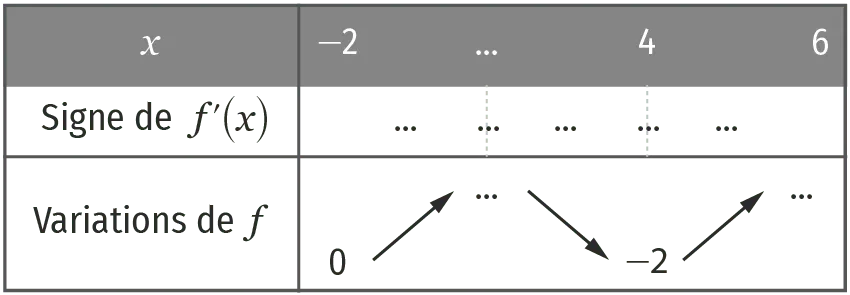
1. À l'aide des informations précédentes, compléter le tableau ci‑dessous grâce notre outil d'édition d'image.
2. Donner le nombre de solutions de l'équation f(x)=0.
3. Déterminer graphiquement la valeur de f^{\prime}(2).
4. Déterminer une équation de la tangente à la courbe \mathcal{C}_f au point d'abscisse 2.
On note f^{\prime} la fonction dérivée de la fonction f sur l'intervalle [-2 \: ; 6].
On considère les points \mathrm{A}(0 \: ; 30), \mathrm{B}(2 \: ; 14), \mathrm{D}(4 \: ; -10) et \mathrm{E}(4 \: ; -2). \text{A}, \text{B} et \text{E} sont trois points de la courbe \mathcal{C}_f.
La droite (\text{BD}) est la tangente à la courbe \mathcal{C}_f au point \text{B}.
Les tangentes à la courbe \mathcal{C}_f aux points \text{A} et \text{E} sont parallèles à l'axe des abscisses.
Le zoom est accessible dans la version Premium.
1. À l'aide des informations précédentes, compléter le tableau ci‑dessous grâce notre outil d'édition d'image.
Le zoom est accessible dans la version Premium.
2. Donner le nombre de solutions de l'équation f(x)=0.
3. Déterminer graphiquement la valeur de f^{\prime}(2).
4. Déterminer une équation de la tangente à la courbe \mathcal{C}_f au point d'abscisse 2.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah