Mathématiques 1re Techno
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 3
Cours 1
Variations d'une fonction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A
Taux de variation en un point
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Soit f une fonction définie sur un intervalle \text{I} et a un nombre réel appartenant à \text{I}.
On appelle taux de variation de f au point d'abscisse a (ou entre a et a + h) le nombre \tau=\frac{f(a+h)-f(a)}{h}, où h est un nombre réel quelconque différent de 0 tel que a+h \in \mathrm{I}.
On appelle taux de variation de f au point d'abscisse a (ou entre a et a + h) le nombre \tau=\frac{f(a+h)-f(a)}{h}, où h est un nombre réel quelconque différent de 0 tel que a+h \in \mathrm{I}.
Remarque
Le taux de variation s'écrit aussi \frac{\Delta f}{\Delta x}.
Notation
On utilise la lettre grecque \tau qui se prononce « tau ».
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Soit f la fonction, qui à tout réel x, associe le nombre f(x)=x^{3}.
Le taux de variation de f entre les valeurs 0 et 0 + 5 est le nombre :
Le taux de variation de f entre les valeurs 0 et 0 + 5 est le nombre :
\tau=\frac{f(0+5)-f(0)}{5}=\frac{5^{3}-0^{3}}{5}=25.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B
Point de vue graphique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Le taux de variation d'une fonction f entre les valeurs a et a + h est le coefficient directeur de la droite passant par \mathrm{A}(a \: ; f(a)) et \mathrm{B}(a+h \: ; f(a+h)).


Remarque
Le coefficient directeur de la droite (\mathrm{AB}) vaut : m=\frac{y_{\mathrm{B}}-y_{\mathrm{A}}}{x_{\mathrm{B}}-x_{\mathrm{A}}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le coefficient directeur de la droite passant par les points \mathrm{A}(a \: ; f(a)) et \mathrm{B}(a+h \: ; f(a+h)) s'écrit \frac{y_{\mathrm{B}}-y_{\mathrm{A}}}{x_{\mathrm{B}}-x_{\mathrm{A}}}=\frac{f(a+h)-f(a)}{a+h-a}=\frac{f(a+h)-f(a)}{h}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
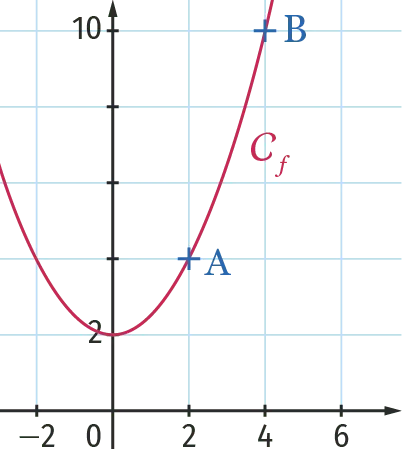
Soit f la fonction définie sur \R par f(x)=0,5 x^{2}+2. On note C_f sa courbe représentative dans le repère ci‑dessous.
On a f(2)=0,5 \times 2^{2}+2=4 donc \mathrm{A}(2 ; 4) \in \mathcal{C}_{f}.
Par ailleurs, f(4)=0,5 \times 4^{2}+2=10 donc \mathrm{B}(4 ; 10) \in \mathcal{C}_{f}.
Le taux de variation de f entre 2 et 4 est donc le coefficient directeur de la droite (\mathrm{AB}): \frac{y_{\mathrm{B}}-y_{\mathrm{A}}}{x_{\mathrm{B}}-x_{\mathrm{A}}}=\frac{10-4}{4-2}=\frac{6}{2}=3.
On a f(2)=0,5 \times 2^{2}+2=4 donc \mathrm{A}(2 ; 4) \in \mathcal{C}_{f}.
Par ailleurs, f(4)=0,5 \times 4^{2}+2=10 donc \mathrm{B}(4 ; 10) \in \mathcal{C}_{f}.
Le taux de variation de f entre 2 et 4 est donc le coefficient directeur de la droite (\mathrm{AB}): \frac{y_{\mathrm{B}}-y_{\mathrm{A}}}{x_{\mathrm{B}}-x_{\mathrm{A}}}=\frac{10-4}{4-2}=\frac{6}{2}=3.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 1
Calculer un taux de variation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soit f la fonction définie, pour tout réel x, par f(x)=1-x^{3}. Soient \text{A} et \text{B} les points d'abscisses -1 et 3.
Calculer le taux de variation de f entre -1 et 3.
Calculer le taux de variation de f entre -1 et 3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
f(\color{#CE422B}-1\color{black})=1-(-1)^{3}=1+1=\color{#5EB45E}2 donc le point \text{A} a pour coordonnées (\color{#CE422B}-1\color{black} \: ; \color{#5EB45E}2\color{black}).
f(\color{#CE422B}3\color{black})=1-3^{3}=1-27=\color{#5EB45E}-26 donc le point \text{B} a pour coordonnées (\color{#CE422B}3\color{black} \: ; \color{#5EB45E}-26\color{black}).
Le taux de variation de f entre -1 et 3 vaut m=\frac{y_{\mathrm{B}}-y_{\mathrm{A}}}{x_{\mathrm{B}}-x_{\mathrm{A}}}=\frac{-26-2}{3-(-1)}=-7.
Pour s'entraîner : exercices et
f(\color{#CE422B}3\color{black})=1-3^{3}=1-27=\color{#5EB45E}-26 donc le point \text{B} a pour coordonnées (\color{#CE422B}3\color{black} \: ; \color{#5EB45E}-26\color{black}).
Le taux de variation de f entre -1 et 3 vaut m=\frac{y_{\mathrm{B}}-y_{\mathrm{A}}}{x_{\mathrm{B}}-x_{\mathrm{A}}}=\frac{-26-2}{3-(-1)}=-7.
Pour s'entraîner : exercices et
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. On détermine les coordonnées des points \text{A} et \text{B}.
2. On calcule le coefficient directeur m de la droite (\mathrm{AB}).
2. On calcule le coefficient directeur m de la droite (\mathrm{AB}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C
Lien avec les variations de la fonction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Soit f une fonction monotone sur un intervalle \text{I}. Alors les taux de variation entre deux valeurs de cet intervalle sont de signe constant (tous positifs ou tous négatifs).
Plus précisément :
Plus précisément :
- si f est croissante sur \text{I}, alors les taux de variation de f sur \text{I} sont positifs ;

- si f est décroissante sur \text{I}, alors les taux de variation de f sur \text{I} sont négatifs.
À visualiser dans ce module GeoGebra :
Remarque
Une fonction f est monotone sur un intervalle \text{I} lorsque f ne change pas de variation sur \text{I} (f reste soit croissante, soit décroissante).
Remarque
La condition monotone est essentielle ici.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- f étant croissante sur \text{I}, alors, quels que soient les nombres a et a + h de \text{I}, les droites joignant deux points de la courbe ont des coefficients directeurs positifs et donc les taux de variation sont positifs.
- f étant décroissante sur \text{I}, alors, quels que soient les nombres a et a + h de \text{I}, les droites joignant deux points de la courbe ont des coefficients directeurs négatifs et donc les taux de variation sont négatifs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
La fonction x \mapsto 3-x^{2} est décroissante sur l'intervalle [0 \: ;+\infty[.
Le taux de variation entre deux valeurs quelconques est donc négatif. Par exemple :
Le taux de variation entre deux valeurs quelconques est donc négatif. Par exemple :
- entre 1 et 5: \tau=\frac{\left(3-5^{2}\right)-\left(3-1^{2}\right)}{5-1}=-6 \lt 0 \: ;
- entre 10 et 12: \tau=\frac{\left(3-12^{2}\right)-\left(3-10^{2}\right)}{12-10}=-22 \lt 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 2
Utiliser le lien entre taux de variation et variations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soit f une fonction dont on donne le tableau de variations ci‑dessous.

Sans calcul, donner le signe du taux de variation de f entre 0 et 5, puis le calculer.

Sans calcul, donner le signe du taux de variation de f entre 0 et 5, puis le calculer.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le tableau nous donne :
- le sens de variation de la fonction ;
- les images de 0 et de 5 par f.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

