Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 3
Entraînement 3
Point de vue global : fonction dérivée et applications
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 64
[Calculer.]
Associer, à chaque fonction, sa fonction dérivée.
: f_{1}(x)=-2 x^{3}+7 x^{2}+x+1
: f_{2}(x)=-2 x^{2}+7 x+1
: f_{3}(x)=-2 x^{2}+7
: f_{2}(x)=-2 x^{2}+7 x+1
: f_{3}(x)=-2 x^{2}+7
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 65
[Calculer.]
Soit f la fonction définie pour tout réel x par :
1. Déterminer, pour tout réel x, une expression de f^{\prime}(x).
2. Calculer les nombres dérivés f^{\prime}(0) et f^{\prime}(2) et interpréter graphiquement ces deux nombres.
f(x)=x^{2}-4 x+1.
On note f^{\prime} la fonction dérivée de la fonction f.
1. Déterminer, pour tout réel x, une expression de f^{\prime}(x).
2. Calculer les nombres dérivés f^{\prime}(0) et f^{\prime}(2) et interpréter graphiquement ces deux nombres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 66
[Calculer.]
Soit f la fonction définie pour tout réel x par :
1. Calculer f(0).
2. Déterminer, pour tout réel x, une expression de f^{\prime}(x).
3. Calculer le nombre dérivé f^{\prime}(0) puis déterminer une équation de la tangente à la courbe représentative de f au point d'abscisse 0.
f(x)=\frac{3}{2} x^{2}-\frac{1}{4} x+5.
On note f^{\prime} la fonction dérivée de la fonction f.
1. Calculer f(0).
2. Déterminer, pour tout réel x, une expression de f^{\prime}(x).
3. Calculer le nombre dérivé f^{\prime}(0) puis déterminer une équation de la tangente à la courbe représentative de f au point d'abscisse 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 67
[Communiquer.]
On considère la fonction f définie, pour tout réel x, par f(x)=-0,5 x^{3}+0,5 x+1
Un élève affirme que les tangentes à la courbe représentative de f aux points d'abscisses -1 et 1 sont parallèles.
Discuter cette affirmation.
Un élève affirme que les tangentes à la courbe représentative de f aux points d'abscisses -1 et 1 sont parallèles.
Discuter cette affirmation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 68
[Calculer.]
Dans chaque cas, déterminer l'expression de f^{\prime}, la fonction dérivée de f, puis l'équation réduite de la tangente à la courbe représentative de f au point d'abscisse a.
1. f(x)=x^{2}+x+1 et a=0.
2. f(x)=x^{3}-7 x et a=-1.
3. f(x)=x^{3}+x^{2} et a=2.
1. f(x)=x^{2}+x+1 et a=0.
2. f(x)=x^{3}-7 x et a=-1.
3. f(x)=x^{3}+x^{2} et a=2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 69
[Représenter.]
On considère la fonction f définie sur [0 \: ; 3] par :
1. Déterminer, pour tout x \in[0 \: ; 3], une expression de f^{\prime}(x).
2. Résoudre sur [0 \: ; 3] l'équation f^{\prime}(x)=0.
3. Grâce à notre outil d'édition d'image, compléter le tableau suivant
f(x)=2 x^{2}-4 x.
On note f^{\prime} la fonction dérivée de la fonction f.
1. Déterminer, pour tout x \in[0 \: ; 3], une expression de f^{\prime}(x).
2. Résoudre sur [0 \: ; 3] l'équation f^{\prime}(x)=0.
3. Grâce à notre outil d'édition d'image, compléter le tableau suivant
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 70
Le zoom est accessible dans la version Premium.
[Chercher.]
Le zoom est accessible dans la version Premium.
On a représenté ci‑dessous le tableau de signe de la dérivée f^{\prime} d'une fonction f définie sur [0 \: ; 8].
1. À l'aide de la calculatrice graphique, identifier la fonction f parmi les trois propositions suivantes.
a. f(x)=0,5 x^{2}-3 x+7,5
b. f(x)=-0,5 x^{2}+2 x+1
c. f(x)=-0,5 x^{2}+3 x
2. Construire le tableau de variations de f.
Le zoom est accessible dans la version Premium.
1. À l'aide de la calculatrice graphique, identifier la fonction f parmi les trois propositions suivantes.
a. f(x)=0,5 x^{2}-3 x+7,5
b. f(x)=-0,5 x^{2}+2 x+1
c. f(x)=-0,5 x^{2}+3 x
2. Construire le tableau de variations de f.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 71
[Calculer.]
On considère la fonction f définie, pour tout réel x, par f(x)=3,5 x^{2}-14 x+1.
On note f^{\prime} la fonction dérivée de la fonction f.
1. Déterminer, pour tout réel x, une expression de f^{\prime}(x) en fonction de x.
2. Étudier, pour tout réel x, le signe de f^{\prime}(x).
3. En déduire les variations de f sur \R.
On note f^{\prime} la fonction dérivée de la fonction f.
1. Déterminer, pour tout réel x, une expression de f^{\prime}(x) en fonction de x.
2. Étudier, pour tout réel x, le signe de f^{\prime}(x).
3. En déduire les variations de f sur \R.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 72
[Calculer.]
Reprendre l'exercice précédent avec la fonction g définie, pour tout réel x, par g(x)=-3 x^{2}+16 x-3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 73
[Calculer.]
On considère la fonction f définie, pour tout réel x, par f(x)=x^{3}+4 x
On note f^{\prime} la fonction dérivée de la fonction f.
1. Déterminer, pour tout réel x, une expression de f^{\prime}(x) en fonction de x.
2. Étudier, pour tout réel x, le signe de f^{\prime}(x).
3. En déduire les variations de f sur \R.
On note f^{\prime} la fonction dérivée de la fonction f.
1. Déterminer, pour tout réel x, une expression de f^{\prime}(x) en fonction de x.
2. Étudier, pour tout réel x, le signe de f^{\prime}(x).
Remarque
La somme de deux nombres positifs est positive.
3. En déduire les variations de f sur \R.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 74
[Calculer.]
Reprendre l'exercice précédent avec la fonction g définie, pour tout réel x, par g(x)=-x^{3}-7.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 75
[Représenter.]
Suite à une épidémie dans une région, le nombre de personnes malades t jours après l'apparition des premiers cas est modélisé par f(t)=45 t^{2}-t^{3}, pour tout t appartenant à [0 \: ; 45].
1. Déterminer le nombre de personnes malades prévu par ce modèle au bout de 20 jours.
2. Montrer que pour tout t appartenant à [0 \: ; 45] :
3. Déterminer le signe de f^{\prime}(t) sur [0 \: ; 45].
4. Dresser le tableau de variations de f sur l'intervalle [0 \: ; 45].
5. Déterminer le jour où le nombre de personnes malades est maximal durant cette période de 45 jours et préciser le nombre de personnes alors malades.
Le zoom est accessible dans la version Premium.
1. Déterminer le nombre de personnes malades prévu par ce modèle au bout de 20 jours.
2. Montrer que pour tout t appartenant à [0 \: ; 45] :
f^{\prime}(t)=3 t(30-t).
3. Déterminer le signe de f^{\prime}(t) sur [0 \: ; 45].
4. Dresser le tableau de variations de f sur l'intervalle [0 \: ; 45].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
5. Déterminer le jour où le nombre de personnes malades est maximal durant cette période de 45 jours et préciser le nombre de personnes alors malades.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans la vie professionnelle
Le technicien d'analyses biomédicales effectue des analyses sur des prélèvements humains (sang, urine, selles, etc.) afin de permettre aux médecins d'établir un diagnostic. Pour cela, le technicien prépare les produits, manipule les échantillons, puis rédige une conclusion chiffrée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 76
[Modéliser.]
Le zoom est accessible dans la version Premium.
Étude d'une fonction de degré 2
On modélise le chiffre d'affaires trimestriel, en milliers d'euros, d'une entreprise hôtelière depuis le premier trimestre 2020 par la fonction f définie sur l'intervalle [0 \: ; 16] par f(x)=0,8 x^{2}-10 x+200 où x s'exprime en trimestres écoulés depuis le 1er janvier 2020.
1. Quel est le chiffre d'affaires de l'entreprise au 1er janvier 2020 ? Au 1er janvier 2021 ?
2. a. Déterminer, pour tout x \in[0 \: ; 16], une expression de f^{\prime}(x).
b. Étudier le signe de f^{\prime}(x) sur l'intervalle [0 \: ; 16].
c. En déduire le tableau de variations de f sur l'intervalle [0 \: ; 16].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
3. À partir de quel moment l'entreprise voit‑elle son chiffre d'affaires s'améliorer ?
4. En traçant la courbe représentative de f, à partir de quelle date peut‑on prévoir que le chiffre d'affaires sera supérieur à celui de début 2020 ? Justifier par le calcul.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 77
[Calculer.]
On a représenté ci‑dessous une fonction f définie et dérivable sur [1 \: ; 8].
Étudier, pour tout x \in[1 \: ; 8], le signe de f^{\prime}(x).
Le zoom est accessible dans la version Premium.
Étudier, pour tout x \in[1 \: ; 8], le signe de f^{\prime}(x).
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Aide
On pourra utiliser le lien entre le signe de f^{\prime} et les variations de f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 78
[Communiquer.]
Parmi les courbes ci‑dessous, une seule représente la dérivée de la fonction f: x \mapsto-3 x^{2}+2 x+5.
Laquelle ?
Laquelle ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 79
[Représenter.]
On donne ci‑dessous le tableau de signe de la dérivée f^{\prime} d'une fonction f définie sur \R.
Parmi les trois courbes suivantes, une seule correspond à la représentation graphique de la fonction f. Laquelle ?
1.
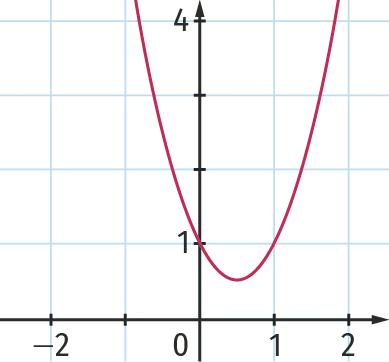
2.
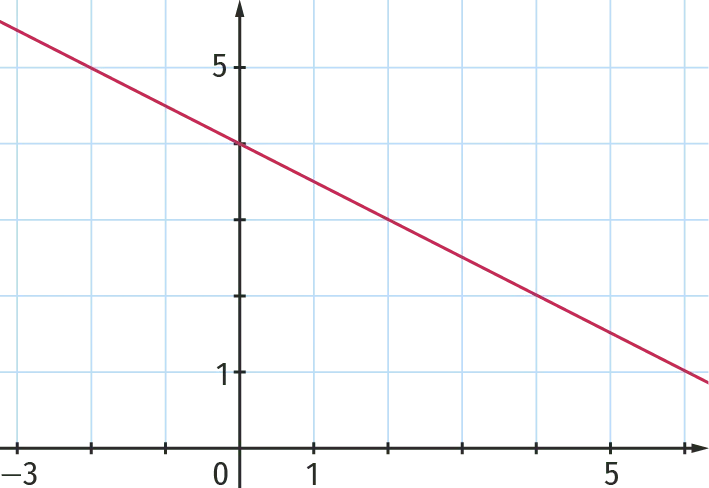
3.
Le zoom est accessible dans la version Premium.
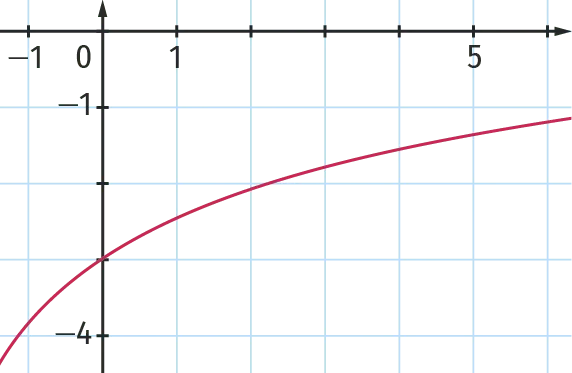
Parmi les trois courbes suivantes, une seule correspond à la représentation graphique de la fonction f. Laquelle ?
1.
Le zoom est accessible dans la version Premium.
2.
Le zoom est accessible dans la version Premium.
3.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 80
[Représenter.]
Les courbes \mathcal{C}_1, \mathcal{C}_2 et \mathcal{C}_3 représentent trois fonctions f_1, f_2 et f_3.
Associer, à chacune d'elles, la courbe représentative de sa fonction dérivée, \mathcal{L}_1, \mathcal{L}_2 ou \mathcal{L}_3.
\mathcal{C}_2 :
\mathcal{C}_3 :
Associer, à chacune d'elles, la courbe représentative de sa fonction dérivée, \mathcal{L}_1, \mathcal{L}_2 ou \mathcal{L}_3.
Courbes des fonctions f_1, f_2 et f_3
Courbes des dérivées f_{1}^{\prime}, f_{2}^{\prime} et f_{3}^{\prime}
Le zoom est accessible dans la version Premium.
Courbes des dérivées f_{1}^{\prime}, f_{2}^{\prime} et f_{3}^{\prime}
Le zoom est accessible dans la version Premium.
\mathcal{C}_1 :
\mathcal{C}_2 :
\mathcal{C}_3 :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 81
[Raisonner.]
Les courbes représentatives des fonctions f et g définies, pour tout réel x, par f(x)=x^{2}-2 x+5 et g(x)=-x^{2}+12 x-32 admettent deux tangentes parallèles, comme l'illustre la figure ci‑dessous.
1. Donner deux nombres a et b tels que f^{\prime}(a)=g^{\prime}(b).
2. Déterminer l'équation réduite de la tangente à la courbe représentative de f au point d'abscisse a.
3. Déterminer l'équation réduite de la tangente à la courbe représentative de g au point d'abscisse b.
Le zoom est accessible dans la version Premium.
1. Donner deux nombres a et b tels que f^{\prime}(a)=g^{\prime}(b).
2. Déterminer l'équation réduite de la tangente à la courbe représentative de f au point d'abscisse a.
3. Déterminer l'équation réduite de la tangente à la courbe représentative de g au point d'abscisse b.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 82
[Modéliser.]
On considère les fonctions f: x \mapsto x^{2}-3 x+3 et g: x \mapsto x^{3}-4,5 x^{2}+5 x-0,5 définies sur \R.
1. Pour tout réel x, déterminer une expression de f^{\prime}(x) et de g^{\prime}(x).
2. En déduire que ces deux courbes ont une tangente commune au point d'abscisse 1.
1. Pour tout réel x, déterminer une expression de f^{\prime}(x) et de g^{\prime}(x).
2. En déduire que ces deux courbes ont une tangente commune au point d'abscisse 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 83
[Représenter.]
Soit f la fonction définie pour tout réel x par :
1. Déterminer, pour tout réel x, une expression de f^{\prime}(x).
2. Prouver que, pour tout réel a, on a f^{\prime}(-a)=f^{\prime}(a).
3. Interpréter graphiquement ce résultat.
f(x)=-2 x^{3}-4 x+1
1. Déterminer, pour tout réel x, une expression de f^{\prime}(x).
2. Prouver que, pour tout réel a, on a f^{\prime}(-a)=f^{\prime}(a).
3. Interpréter graphiquement ce résultat.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 84
[Représenter.]
Soit f la fonction définie sur [-10 \: ; 20] par :
On admet que f est dérivable sur [-10 \: ; 20] et on note f^{\prime} la fonction dérivée de f.
1. a. Montrer que pour tout x \in [-10 \: ; 20] :
1. b. Montrer que pour tout x \in [-10 \: ; 20] :
2. Déterminer le tableau de variations de f sur [-10 \: ; 20].
f(x)=(x-1)\left(x^{2}-2 x-26\right).
On admet que f est dérivable sur [-10 \: ; 20] et on note f^{\prime} la fonction dérivée de f.
1. a. Montrer que pour tout x \in [-10 \: ; 20] :
f^{\prime}(x)=3 x^{2}-6 x-24.
1. b. Montrer que pour tout x \in [-10 \: ; 20] :
f^{\prime}(x)=3(x-4)(x+2).
Aide
On pourra développer, pour tout x \in [-10 \: ; 20], la seconde expression.
2. Déterminer le tableau de variations de f sur [-10 \: ; 20].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 85
Exercice inversé
Proposer une fonction polynôme de degré 2 dont le tableau de variations est le suivant.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 86
Exercice inversé
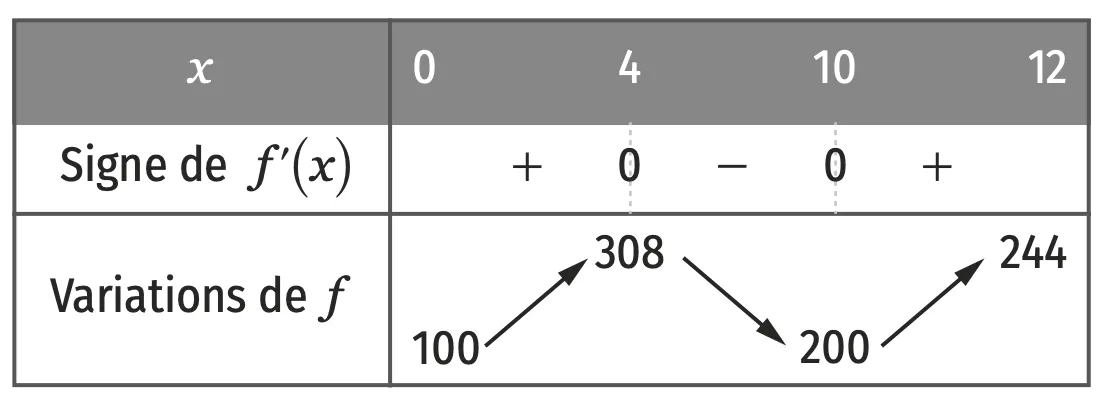
Proposer une fonction polynôme de degré 3, de
la forme x^{3}+b x^{2}+c x+d, dont le tableau de variations est le suivant.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah