Mathématiques Terminale Bac Pro - Cahier
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 8
Avant de commencer
Trigonométrie
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'objectif de ce chapitre est d'apprendre à résoudre certaines équations trigonométriques et de faire découvrir un outil permettant d'ajouter ou de soustraire des tensions ou des intensités sinusoïdales de même fréquence. Son introduction s'appuie sur des exemples concrets issus du domaine professionnel ou de la physique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Une table de mixage est un instrument permettant de moduler le son afin de créer des sonorités uniques. Les signaux de base sont créés avec des fonctions trigonométriques puis ils peuvent être modifiés (changements de fréquences ou d'amplitudes par exemple) grâce à des algorithmes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rappels de première
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Cercle trigonométrique
On se place dans un repère orthonormé du plan d'origine \text{O}. Le cercle trigonométrique \text{C} est le cercle de centre \text{O}, de rayon 1 et orienté dans le sens direct (sens inverse des aiguilles d'une montre).Sinus et cosinus d'un nombre réel

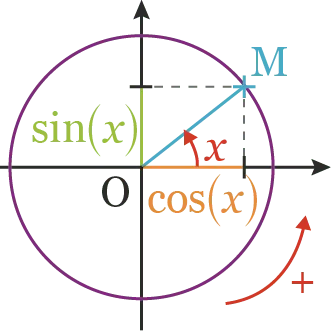
Soit \text{M} un point appartenant au cercle trigonométrique.
Le cosinus du nombre réel x, noté \textrm{cos}(x), est l᾽abscisse du point \text{M}.
Le sinus du nombre réel x, noté \text{sin}(x), est l'ordonnée du point \text{M}.
Propriétés : Pour tout réel x, on a :
1. -1 \leqslant \cos (x) \leqslant 1 et -1 \leqslant \sin (x) \leqslant 1
2. \cos (x+2 \pi)=\cos (x) et \sin (x+2 \pi)=\sin (x)
3. \cos ^{2}(x)+\sin ^{2}(x)=1
4. \cos (x)=\sin \left(x+\frac{\pi}{2}\right)
Valeurs remarquables de cosinus et de sinus

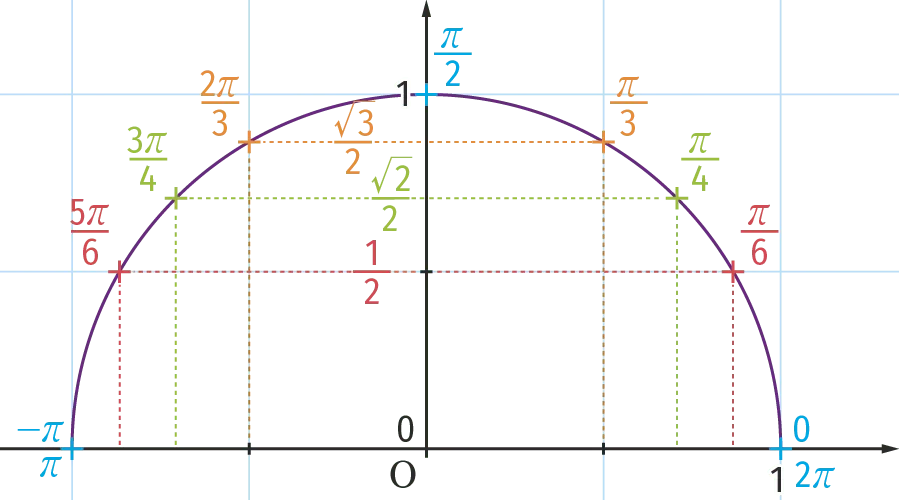
| x en degré | 0° | 30° | 45° | 60° | 900° | 180° |
| x en radian | 0 | \frac{\pi}{6} | \frac{\pi}{4} | \frac{\pi}{3} | \frac{\pi}{2} | \pi |
| \sin(x) | 0 | \frac{1}{2} | \frac{\sqrt{2}}{2} | \frac{\sqrt{3}}{2} | 1 | 0 |
| \cos(x) | 1 | \frac{\sqrt{3}}{2} | \frac{\sqrt{2}}{2} | \frac{1}{2} | 0 | -1 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Validation des acquis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1
Pour chaque question, choisir la ou les bonnes réponses.
1. Sur le cercle trigonométrique ci-dessous, \text{R} est le point image de :

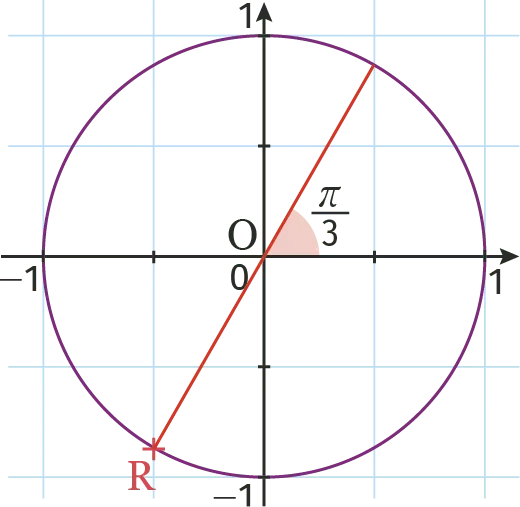
2. \cos \left(\frac{5 \pi}{6}\right)=\ldots
3. \sin \left(\frac{3 \pi}{2}\right)=\ldots
4. \cos \left(\frac{\pi}{4}\right)=\ldots
5. \cos \left(\frac{4 \pi}{3}\right)=\ldots
6. \sin \left(\frac{\pi}{4}+2 \pi\right)=\ldots
1. Sur le cercle trigonométrique ci-dessous, \text{R} est le point image de :


2. \cos \left(\frac{5 \pi}{6}\right)=\ldots
3. \sin \left(\frac{3 \pi}{2}\right)=\ldots
4. \cos \left(\frac{\pi}{4}\right)=\ldots
5. \cos \left(\frac{4 \pi}{3}\right)=\ldots
6. \sin \left(\frac{\pi}{4}+2 \pi\right)=\ldots
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
