Mathématiques Terminale Bac Pro - Cahier
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Poursuite d'études
Fonctions logarithme népérien et exponentielle
✔ Utiliser les propriétés opératoires de la fonction \bm{\ln} pour résoudre une équation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés
Soit a, b et k des nombres réels strictement positifs.- \ln (a \times b)=\ln (a)+\ln (b).
- \ln \left(\frac{1}{b}\right)=-\ln (b) et \ln \left(\frac{a}{b}\right)=\ln (a)-\ln (b).
- \ln \left(a^{k}\right)=k \times \ln (a) et en particulier \ln \left(a^{2}\right)=2 \times \ln (a).
Remarque
Ces propriétés sont les mêmes que pour la fonction \log.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice corrigé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Déterminer le plus grand entier naturel n tel que 1{,}25^{n} \leqslant 20.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
La fonction \ln étant strictement croissante
sur ] 0 \:;+\infty[, 1{,}25^{n} \leqslant 20 équivaut à \ln \left(1{,}25^{n}\right) \leqslant \ln (20).
Comme \ln \left(1{,}25^{n}\right)=n \times \ln (1{,}25), alors on a n \times \ln (1{,}25) \leqslant \ln (20) donc n \leqslant \frac{\ln (20)}{\ln (1{,}25)} car \ln (1{,}25)>0.
On calcule \frac{\ln (20)}{\ln (1{,}25)} \approx 13{,}4. Le plus grand entier naturel n tel que 1,25^{n} \leqslant 20 est donc 13.
On peut vérifier à l'aide de la calculatrice : 1{,}25^{13} \approx 18{,}19 et 1{,}25^{14} \approx 22{,}74.
Comme \ln \left(1{,}25^{n}\right)=n \times \ln (1{,}25), alors on a n \times \ln (1{,}25) \leqslant \ln (20) donc n \leqslant \frac{\ln (20)}{\ln (1{,}25)} car \ln (1{,}25)>0.
On calcule \frac{\ln (20)}{\ln (1{,}25)} \approx 13{,}4. Le plus grand entier naturel n tel que 1,25^{n} \leqslant 20 est donc 13.
On peut vérifier à l'aide de la calculatrice : 1{,}25^{13} \approx 18{,}19 et 1{,}25^{14} \approx 22{,}74.
Méthode
On procède de la même manière qu'avec la fonction \log.
- On utilise la croissance de \ln pour écrire : 1,25^{n} \leqslant 20 \Leftrightarrow \ln \left(1,25^{n}\right) \leqslant \ln (20).
- On applique les propriétés opératoires de \ln pour écrire \ln \left(1,25^{n}\right) comme le produit de deux nombres.
- On résout l'inéquation obtenue comme une inéquation du premier degré. Attention au signe quand on divise par un logarithme.
- On utilise la calculatrice pour obtenir une valeur approchée des logarithmes népériens.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 13
Exprimer, en fonction de \ln(2) et \ln(3) les expressions suivantes.
1. \ln (3 \times 2)
2. \ln (2 \times 27)
3. \ln \left(\frac{2}{9}\right)
4. \ln (9 \times 4 \times 27)
1. \ln (3 \times 2)
2. \ln (2 \times 27)
3. \ln \left(\frac{2}{9}\right)
4. \ln (9 \times 4 \times 27)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 14
Exprimer, en fonction de x, \ln(2) et \ln(3) les expressions suivantes.
1. \mathrm{A}=\ln \left(\frac{2}{9^{x}}\right)
2. \mathrm{B}=\ln \left(\frac{2^{x}}{3}\right)
3. \mathrm{C}=\ln (6)-\ln (2)
4. \mathrm{D}=\ln \left(8 \times 1,5^{x}\right)
5. \mathrm{E}=\ln \left(12^{x}\right)-\ln \left(4^{x}\right)
6. \mathrm{F}=\ln \left(\frac{3}{4}\right)+\ln \left(\frac{2}{3}\right)
1. \mathrm{A}=\ln \left(\frac{2}{9^{x}}\right)
2. \mathrm{B}=\ln \left(\frac{2^{x}}{3}\right)
3. \mathrm{C}=\ln (6)-\ln (2)
4. \mathrm{D}=\ln \left(8 \times 1,5^{x}\right)
5. \mathrm{E}=\ln \left(12^{x}\right)-\ln \left(4^{x}\right)
6. \mathrm{F}=\ln \left(\frac{3}{4}\right)+\ln \left(\frac{2}{3}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 15
Utiliser les propriétés opératoires du logarithme pour simplifier les expressions suivantes.
1. \text{A}=\ln \left(\frac{0,75^{x}}{2}\right)
2. \mathrm{B}=\ln \left((x-1)^{2}\right)-\ln (x-1)
3. \mathrm{C}=\ln \left(\frac{1}{2}\right)+\ln \left(\frac{1}{2}\right)
4. \mathrm{D}=\ln \left(1,4^{x}\right)
1. \text{A}=\ln \left(\frac{0,75^{x}}{2}\right)
2. \mathrm{B}=\ln \left((x-1)^{2}\right)-\ln (x-1)
3. \mathrm{C}=\ln \left(\frac{1}{2}\right)+\ln \left(\frac{1}{2}\right)
4. \mathrm{D}=\ln \left(1,4^{x}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 16
Soit f la fonction définie sur ] 0 \:;+\infty[ par f: x \mapsto \ln \left(x^{2}\right).
Simplifier l'expression de f et en déduire l'expression de sa fonction dérivée.
Simplifier l'expression de f et en déduire l'expression de sa fonction dérivée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 17
Donner une valeur approchée, arrondie au dixième, de la solution de chacune de ces équations.
1. 2^x = 1
2. 0{,}1^{x}=\mathrm{e}
3. \mathrm{e}^x = 2
4. 1{,}2^x = 1{,}44
1. 2^x = 1
2. 0{,}1^{x}=\mathrm{e}
3. \mathrm{e}^x = 2
4. 1{,}2^x = 1{,}44
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 18
Donner une valeur approchée, arrondie au dixième, de la solution de chacune de ces équations.
1. \left(\frac{2}{3}\right)^{n}=1
2. 2 \times 5^{n}=4
3. 2 \times 3^{n}=9
1. \left(\frac{2}{3}\right)^{n}=1
2. 2 \times 5^{n}=4
3. 2 \times 3^{n}=9
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 19
Dans chaque cas, déterminer le plus grand entier n vérifiant l'inéquation donnée.
1. 2{,}1^{n} \leqslant 8
2. 4 \times 10^{n} \leqslant 200
3. \left(\frac{3}{2}\right)^{n} \leqslant 20
1. 2{,}1^{n} \leqslant 8
2. 4 \times 10^{n} \leqslant 200
3. \left(\frac{3}{2}\right)^{n} \leqslant 20
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 20
Dans chaque cas, déterminer le plus petit entier n vérifiant l'inéquation donnée.
1. 5{,}3^{n}>40
2. 4{,}5^{n} \geqslant 18
3. \left(\frac{8}{3}\right)^{n} \geqslant 1
1. 5{,}3^{n}>40
2. 4{,}5^{n} \geqslant 18
3. \left(\frac{8}{3}\right)^{n} \geqslant 1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 21
Résoudre les inéquations suivantes. On arrondira les solutions à 10^{-2} près.
1. 0{,}9^{x}\lt0{,}5
2. 1{,}8^{x}>1{,}9^{2}
3. \left(\frac{4}{5}\right)^{x} \geqslant 0{,}6
4. 4^{x} \leqslant 5^{x}
5. 0{,}1^{x} \lt 0{,}2^{x}
1. 0{,}9^{x}\lt0{,}5
2. 1{,}8^{x}>1{,}9^{2}
3. \left(\frac{4}{5}\right)^{x} \geqslant 0{,}6
4. 4^{x} \leqslant 5^{x}
5. 0{,}1^{x} \lt 0{,}2^{x}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 22
Une quantité augmente de 20 % par heure. Sa valeur au début de l'observation est u_{0}=1.
1. Calculer sa valeur, arrondie au dixième, au bout de cinq heures.
2. On donne l'algorithme suivant, écrit en langage courant.
À quoi sert cet algorithme ?
3. Déterminer la valeur de la variable n à la fin de l'exécution de l'algorithme.
1. Calculer sa valeur, arrondie au dixième, au bout de cinq heures.
2. On donne l'algorithme suivant, écrit en langage courant.
\boxed{
\begin{array} { r|l }
1 & u = 1, n = 0 \\
2 & \text{Tant que } u \lt 6 \text{ faire :} \\
3 & \quad u \leftarrow u \times 1,2 \\
4 & \quad n \leftarrow n+1 \\
5 & \text{Afficher } n \\
\end{array}
}
À quoi sert cet algorithme ?
3. Déterminer la valeur de la variable n à la fin de l'exécution de l'algorithme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 23
Une quantité un diminue de 12 % par an. Sa valeur de départ est u_{0}=1.
1. Calculer sa valeur arrondie à 10^{-1} après quatre ans.
2. On modélise l'évolution de cette quantité dans un tableur.

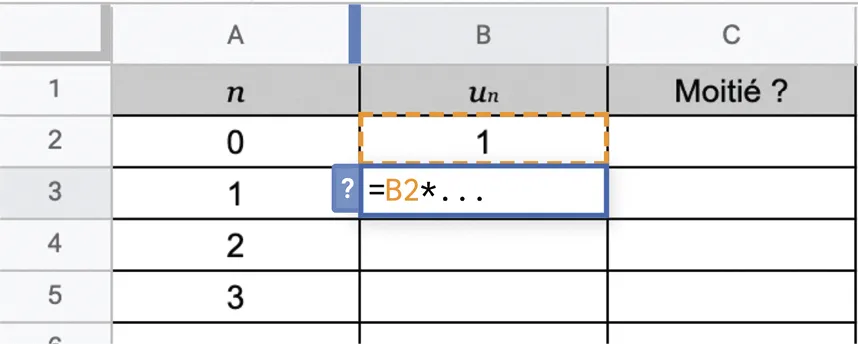
Compléter la formule à entrer en B3 puis à faire glisser vers le bas, afin de calculer la valeur de cette quantité chaque année.
3. Compléter la formule suivante, à entrer en C2, afin qu'elle affiche 1 jusqu'à ce que la quantité observée ait diminué de moitié et 0 ensuite : « =SI(B2 … ; 0 ; 1) ».
4. Déterminer le nombre de 1 obtenus dans la colonne C et interpréter ce résultat.
1. Calculer sa valeur arrondie à 10^{-1} après quatre ans.
2. On modélise l'évolution de cette quantité dans un tableur.


Compléter la formule à entrer en B3 puis à faire glisser vers le bas, afin de calculer la valeur de cette quantité chaque année.
3. Compléter la formule suivante, à entrer en C2, afin qu'elle affiche 1 jusqu'à ce que la quantité observée ait diminué de moitié et 0 ensuite : « =SI(B2 … ; 0 ; 1) ».
4. Déterminer le nombre de 1 obtenus dans la colonne C et interpréter ce résultat.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 24
Soit f et g les fonctions définies sur \R par
f: x \mapsto 5 \times 1,5^{x} et g: x \mapsto 100 \times 0,7^{x}. On a représenté ces deux fonctions dans le repère
ci-dessous.
https://assets.lls.fr/pages/55470040/mattppeinf14-plan-de-travail-1.svg

1. Identifier la courbe représentative de chaque fonction. Justifier la réponse.
2. Résoudre graphiquement l'inéquation f(x) \lt g(x). Arrondir à l'unité.
3. Retrouver ce résultat par le calcul.
https://assets.lls.fr/pages/55470040/mattppeinf14-plan-de-travail-1.svg

1. Identifier la courbe représentative de chaque fonction. Justifier la réponse.
2. Résoudre graphiquement l'inéquation f(x) \lt g(x). Arrondir à l'unité.
3. Retrouver ce résultat par le calcul.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 25
Soit f et g les fonctions définies sur \R par
f: x \mapsto 5 \times 1,4^{x} et g: x \mapsto 8 \times 1,3^{x}.
1. Représenter ces fonctions sur l'écran d'une calculatrice et conjecturer les coordonnées de leur point d'intersection.
2. Recopier et compléter le programme suivant, qui détermine une valeur approchée de l'abscisse de leur point d'intersection.
3. Déterminer la valeur affichée à la fin de l'exécution de ce programme.
1. Représenter ces fonctions sur l'écran d'une calculatrice et conjecturer les coordonnées de leur point d'intersection.
2. Recopier et compléter le programme suivant, qui détermine une valeur approchée de l'abscisse de leur point d'intersection.
\boxed{
\begin{array} { r|l }
1 & x = 0, f = \text{..., } g = \text{...} \\
2 & \text{Tant que } g - f > 0{,}01 \text{ faire :} \\
3 & \quad f \leftarrow \text{...} \\
4 & \quad g \leftarrow \text{...} \\
5 & \text{Afficher } x\\
\end{array}
}
3. Déterminer la valeur affichée à la fin de l'exécution de ce programme.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
