Sommaire
Mes pages
N° Page
Ouverture
p. 1-15
Constitution de la matière à l'échelle microscopique et macroscopique
Ouverturep. 16-17
1. Constitution et transformations de la matière
Testez le chapitre 100 % débloqué
2. Mouvement et interactions
Mouvement et interactions
Ouverturep. 198-199
3. Ondes et signaux
Ondes et signaux
Ouverturep. 250-251
Méthode
Annexes
Rabats de début
Rabats
Lexique
p. 338-339
Rabats de fin
Rabats
/ 339
Vue papier
Animation montrant le basculement entre la vue numérique et la vue papier
Découvrez la vue papier en cliquant ici
Page précédente
Chapitre 11
Exercices

Pour s'entraîner

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

20
Astrophotographie

✔ APP : Maîtriser le vocabulaire du cours

Une astronome amatrice photographie les étoiles avec une longue durée d'exposition.

Placeholder pour Photographie nocturne : traînées lumineuses d'étoiles filantes au-dessus d'un volcan enneigé et d'un arbre.Photographie nocturne : traînées lumineuses d'étoiles filantes au-dessus d'un volcan enneigé et d'un arbre.
Filet d'étoiles

1. Dans quel référentiel les étoiles sont-elles photographiées ?

2. Décrire leur trajectoire.

3. L'étoile polaire est une étoile qui paraît fixe par rapport à la Terre. Identifier cette étoile sur la photographie ci-dessus.

4. En quoi le mouvement apparent des étoiles peut-il être un inconvénient en astrophotographie ?
5. Les astrophotographes professionnels sont équipés de télescopes motorisés qui suivent le mouvement d'une étoile. Expliquer.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

21
Station spatiale internationale

✔ APP : Maîtriser le vocabulaire du cours
✔ REA : Effectuer des calculs littéraux et numériques

Placeholder pour Photographie spatiale de la Station spatiale internationale (ISS) orbitant la Terre. Grands panneaux solaires déployés.Photographie spatiale de la Station spatiale internationale (ISS) orbitant la Terre. Grands panneaux solaires déployés.

La station spatiale internationale (ISS) est une station spatiale en orbite circulaire basse autour de la Terre. Des astronautes internationaux y mènent des expériences de recherche scientifique en milieu spatial. Située à une altitude d'environ 330 km, l'ISS effectue un tour complet en 93 minutes.

1. Quel est le référentiel adapté à l'étude du mouvement de l'ISS ?
2. Décrire le mouvement de l'ISS dans ce référentiel.
3. Calculer la valeur de la vitesse.

4. Décrire la variation du vecteur vitesse.
5. Combien de tours effectue l'ISS en une journée ?


Données

  • Rayon de la Terre : RT 6 370 km.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

22
Performances d'un nageur

✔ MATH : Le modèle du vecteur en physique
✔ REA : Effectuer des mesures. Effectuer des calculs littéraux et numériques

En natation, la chronophotographie permet d'analyser les performances du nageur. L'échelle choisie pour la représentation de la vitesse est : 1 cm 8 ms-1

La chronophotographie
1. Définir le système et le référentiel d'étude.
2. Quelle est la valeur de la vitesse initiale au point ?

3. Calculer la valeur du vecteur vitesse et du plongeur aux points et

4. Tracer le vecteur vitesse et du plongeur aux points , et sur l'image ci-dessous.

5. Comment varient les caractéristiques du vecteur vitesse au cours du mouvement ? Qualifier alors le mouvement du plongeur.

Détails du barème
TOTAL /5,5 pts

0,5 pt
1. Employer les termes du cours.
0,5 0,5 pt
2. Mesurer à la règle la longueur du vecteur et convertir à l'échelle.
1,5 pt
3. Donner la formule littérale puis faire l'application numérique. Exprimer le résultat numérique avec deux chiffres significatifs, en ms-1.
1,5 pt
4. Indiquer le point d'application, l'origine, le sens et la valeur correcte.
1 pt
5. Décrire l'évolution du vecteur vitesse en termes de direction, sens et valeur. Utiliser le vocabulaire approprié pour qualifier le mouvement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

23
Sky Jump à Las Vegas

✔ MATH : Le modèle du vecteur en physique

À Las Vegas, les adeptes de sensations fortes peuvent sauter du haut de la tour Stratosphère pour un saut de 253 mètres, reliés à un câble en acier. Lors des premiers instants (phase 1), le sauteur est en chute libre, puis l'arrivée au sol (phase 2) est freinée par une bobine.

Placeholder pour Saut à l'élastique depuis la tour Stratosphère à Las Vegas. Une personne chute en plein ciel bleu. Photographie.Saut à l'élastique depuis la tour Stratosphère à Las Vegas. Une personne chute en plein ciel bleu. Photographie.

1. Définir le système et le référentiel d'étude.
2. Décrire le mouvement du système lors des deux phases du mouvement.
3. Décrire la variation du vecteur vitesse lors des deux phases du mouvement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

24
La grêle

✔ ANA : Exploiter des informations
✔ MATH : Le modèle du vecteur en physique

Placeholder pour Photographie : grêle tombant sur un toit gris. Gouttes visibles sur les tuiles.Photographie : grêle tombant sur un toit gris. Gouttes visibles sur les tuiles.

La grêle peut avoir des effets dévastateurs pour les habitants et les agriculteurs en raison de la vitesse que les grêlons acquièrent lors de leur chute.
En effet, le grêlon chute avec une vitesse initiale nulle puis accélère jusqu'à atteindre une vitesse limite de 70 kmh-1.

1. Définir le système et le référentiel d'étude.
2. Le système est assimilé à un point matériel. Quel(s) aspect(s) ne peut-on pas aborder lors de cette étude ?
3. Comment évolue le vecteur vitesse lors de la première phase de la chute ?
4. Donner la direction, le sens et la valeur du vecteur vitesse en m·s‑1 lors de la deuxième phase de la chute. Comment qualifier le mouvement lors de cette deuxième phase ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

25
Remontées mécaniques en QCM

✔ MATH : Le modèle du vecteur en physique

On étudie deux remontées mécaniques dans le référentiel terrestre. Un téléski tire des skieurs sur une portion rectiligne à vitesse constante.

1. Le vecteur vitesse du skieur :




Un télésiège décrit une portion de cercle à vitesse constante pour récupérer les skieurs.

2. Le vecteur vitesse du télésiège :




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

26
Les bulles de champagne

✔ ANA : Proposer un protocole

Dans une flûte de champagne, les bulles se créent au niveau des aspérités de la paroi puis remontent verticalement jusqu'à la surface.
On a représenté la chronophotographie d'une bulle lors de son ascension. La durée séparant deux images est égale à 0,050 s.

Chronophotographie d'une bulle
1. Proposer un protocole expérimental qui permettrait de représenter l'évolution de la vitesse de la bulle en fonction du temps.
2. Estimer la taille réelle d'une flûte de champagne et en déduire l'échelle verticale approximative de cette représentation.
3. Comment évolue la valeur de la vitesse au cours du temps ?
4. Estimer la vitesse limite atteinte par la bulle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

27
Copie d'élève à commenter

Proposer une justification pour chaque erreur relevée par le correcteur. Les réponses sont liées à des questions indépendantes.

1. Déterminons la valeur de la vitesse au point 3 :

m/s.


2. Le mouvement est circulaire uniforme donc la variation du vecteur vitesse est nulle.
3. La Lune décrit un cercle dans le référentiel qui est centré sur la Terre et appelé référentiel terrestre.

4. Le vecteur vitesse au point considéré est horizontal, vers la droite et a pour valeur 15 m.

5. La vitesse a toujours la même valeur donc le vecteur vitesse est constant.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Apollo 11

✔ APP : Extraire l'information utile

Le 20 juillet 1969, N. Armstrong, M. Collins et B. Aldrin se posaient sur le sol lunaire à bord du module lunaire Apollo. Le mouvement du module lunaire lors de l'alunissage est représenté sur l'image ci‑après.

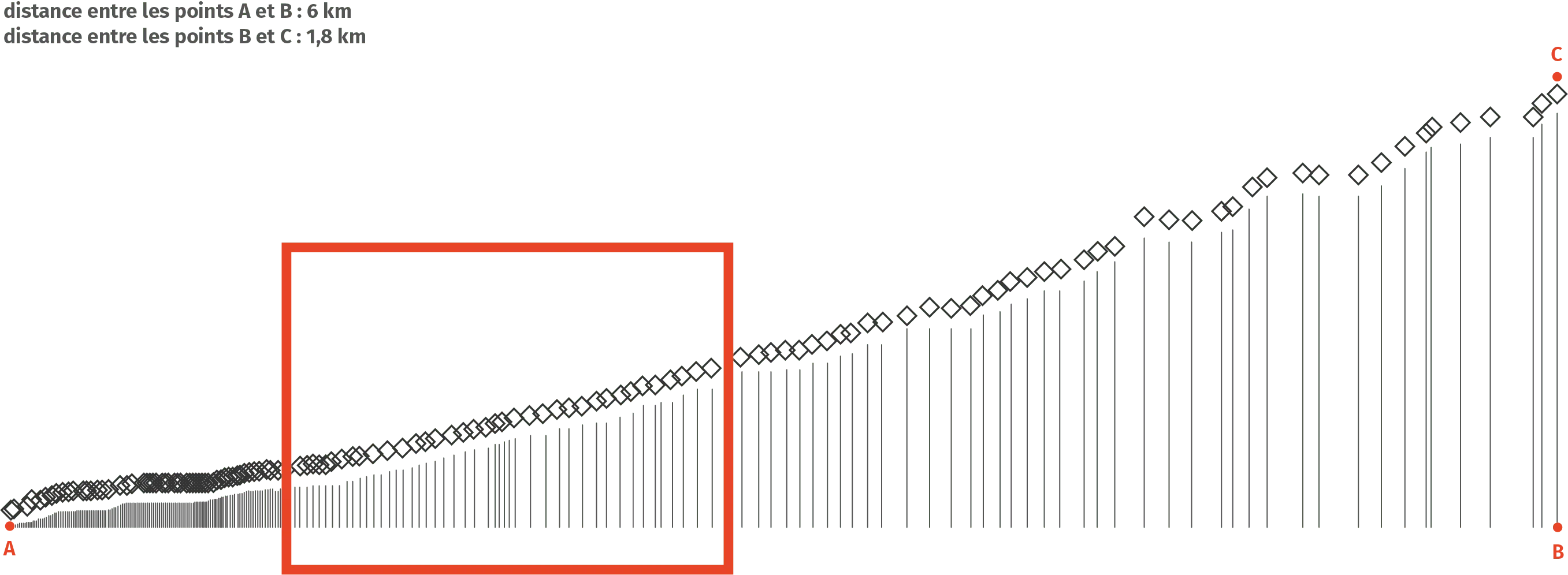
Placeholder pour Graphique montrant une croissance exponentielle de A à C. Distance A-B: 6km, B-C: 1,8km.Graphique montrant une croissance exponentielle de A à C. Distance A-B: 6km, B-C: 1,8km.

1. Dans quel référentiel le mouvement est‑il représenté ?

2. Décrire la partie du mouvement située dans l'encadré en termes de trajectoire et de variation de la vitesse.

3. Estimer la vitesse moyenne du module lors de l'alunissage.
Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille