Enseignement scientifique 1re
Mes Pages
Thème 1 : Une longue histoire de la matière
Ch. 1
Les éléments chimiques
Ch. 2
Des édifices ordonnés : les cristaux
Ch. 3
Une structure complexe : la cellule
Thème 2 : Le Soleil, notre source d'énergie
Ch. 4
Le rayonnement solaire
Ch. 5
Le bilan radiatif terrestre
Ch. 6
Énergie solaire et photosynthèse
Ch. 7
Le bilan thermique du corps humain
Thème 3 : La Terre, un astre singulier
Ch. 8
La forme de la Terre
Ch. 9
L'histoire de l’âge de la Terre
Ch. 10
La Terre dans l’Univers
Thème 4 : Son et musique, porteurs d'information
Ch. 11
Le son, phénomène vibratoire
Ch. 12
Musique et nombres
Ch. 13
Le son, une information à coder
Ch. 14
Entendre la musique
Projet Experimental et Numérique
Livret Maths
Annexes
Thème 1
Objectif Bac
Exercice avec des coups de pouce méthode
Préparation aux épreuves communes de contrôle continu
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1Datation de peintures rupestres
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ÉnoncéCalculatrice autorisée
La grotte Chauvet-Pont d'Arc a été découverte en 1994 dans le cadre d'une exploration spéléologique. Il s'agit de l'un des sites de peintures rupestres les plus remarquables. Les oeuvres peintes datent de l'Aurignacien et témoignent d'une remarquable maîtrise des techniques picturales.
Doc. 1
Grotte Chauvet-Pont d'Arc : détail
de peinture rupestre que l'on date au carbone 14
Doc. 2
La formation du carbone 14
Le temps de demi-vie du carbone 14 est de l'ordre de 5 570 années. Il est continuellement produit dans la haute atmosphère grâce à des réactions nucléaires entre les noyaux des atomes d'azote 14 de l'air et des neutrons d'origine cosmique. Ces réactions maintiennent une teneur constante en ^{14} \mathrm{C} dans l'atmosphère.
Doc. 3
Méthode de datation au carbone 14
Un organisme vivant possède la même concentration en ^{14} \mathrm{C} que l'atmosphère mais à sa mort ses échanges de carbone avec le milieu ambiant cessent et son taux de ^{14} \mathrm{C} décroît alors selon une loi exponentielle.La méthode la plus courante de datation consiste à déterminer le taux de radiocarbone (c'est-à-dire le rapport ^{14} \mathrm{C} / ^{12}\mathrm{C} total) d'un échantillon à l'instant t de mesure.
L'âge de l'échantillon est alors donné par la formule :
t-t_{0}=\dfrac{t_{1 / 2}}{0\text{,}693} \times \ln \left(\dfrac{C_{0}}{C_{t}}\right)
où C_{0} est le taux de carbone 14 dans l'échantillon à l'instant t_{0} de la mort de l'organisme d'où provient l'échantillon \left(C_{0} \approx 10^{-12} \text { et } t_{1 / 2}=\right. 5 570 années).
Remarque : \text{ln} est la fonction logarithme népérien notée « \text{ln} » sur la calculatrice.
1. Donner l'origine du carbone 14 dans l'atmosphère.
2. Comment expliquer la présence de carbone 14 dans les pigments naturels utilisés par les artistes rupestres ?
2. Comment expliquer la présence de carbone 14 dans les pigments naturels utilisés par les artistes rupestres ?
3. Calculer l'âge de ces peintures rupestres dont les échantillons de pigments récoltés donnent un taux mesuré en carbone 14 de : C_{t}=1\text{,}3 \times 10^{-14}.
4. Peut-on confirmer que ces peintures datent de l'Aurignacien, dont la période s'étend de ‑43 000 à ‑29 000 ans ?
4. Peut-on confirmer que ces peintures datent de l'Aurignacien, dont la période s'étend de ‑43 000 à ‑29 000 ans ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Lorsque l'on demande de présenter des réactions nucléaires, toutes les informations nécessaires sont dans l'énoncé.
2. Les pigments sont d'origine végétale. Détailler le processus qui permet au carbone 14 de passer de l'atmosphère (sous forme de \mathrm{CO}_{2}) aux pigments.
3. Attention aux parenthèses pour ce calcul à la calculatrice.
2. Les pigments sont d'origine végétale. Détailler le processus qui permet au carbone 14 de passer de l'atmosphère (sous forme de \mathrm{CO}_{2}) aux pigments.
3. Attention aux parenthèses pour ce calcul à la calculatrice.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3Abondance des éléments chimiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ÉnoncéCalculatrice autorisée
Dans un laboratoire, des étiquettes de micro-échantillons A et B se sont décollées. On cherche à retrouver lequel provient d'une roche et lequel provient de cellules d'origine humaine.
Doc. 1
Abondance massique des éléments chimiques dans le corps humain [a] et la croûte terrestre [b]
[b]
| Élément | Pourcentage massique |
| Fer (\mathrm{Fe}) | 6 % |
| Silicium (\mathrm{Si}) | 28 % |
| Calcium (\mathrm{Ca}) | 4 % |
| Oxygène (0) | 46 % |
| Aluminium (\mathrm{Al}) | 8 % |
| Autres | 8 % |
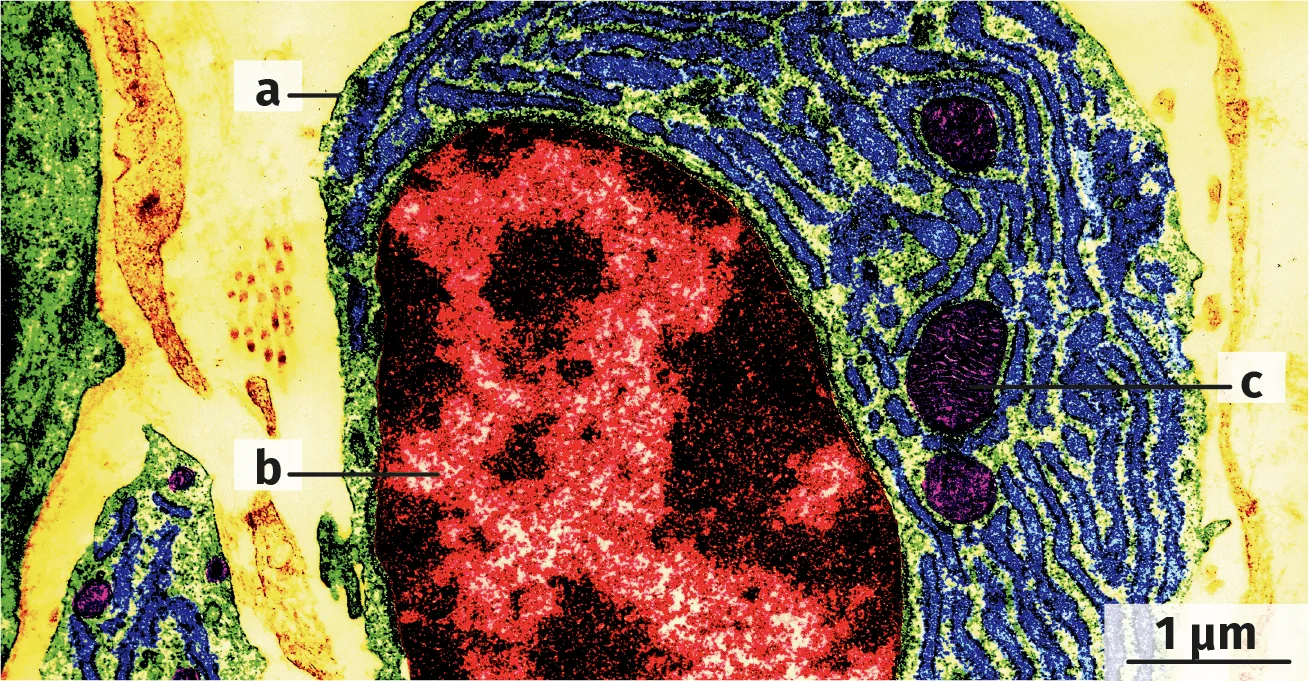
Doc. 2
Microphotographie de cellule humaine
Doc. 3
Représentation schématique d'un lipide
1. Indiquer les deux types de réactions ayant permis, à partir des premiers éléments de l'Univers, de former les autres éléments.
2. Comparer les 3 éléments les plus abondants dans la croûte terrestre avec ceux du corps humain. En déduire une stratégie de résolution du problème.
3. Quels atomes seront les plus abondants (en masse) dans l'échantillon de cellules humaines ?
2. Comparer les 3 éléments les plus abondants dans la croûte terrestre avec ceux du corps humain. En déduire une stratégie de résolution du problème.
3. Quels atomes seront les plus abondants (en masse) dans l'échantillon de cellules humaines ?
4. L'échantillon A pèse 41,67 mg et contient, entre autres : 18 mg d'oxygène, 9,5 mg de silicium et 2,88 mg de calcium. Calculer les pourcentages massiques en O, Si et Ca. Formuler une hypothèse sur la nature de l'échantillon.
5. Le correspond à l'échantillon de cellules humaines. Indiquer avec quel(s) type(s) de microscope(s) on peut obtenir une telle image.
6. Identifier les constituants a, b, c du .
7. Indiquer lequel de ces constituants est composé en grande partie de la molécule du .
5. Le correspond à l'échantillon de cellules humaines. Indiquer avec quel(s) type(s) de microscope(s) on peut obtenir une telle image.
6. Identifier les constituants a, b, c du .
7. Indiquer lequel de ces constituants est composé en grande partie de la molécule du .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Se souvenir des réactions nucléaires apprises.
2. Les deux documents apportent le même type d'information : chercher les 3 pourcentages les plus élevés dans chacun des documents, puis indiquer s'ils concernent les mêmes éléments dans les deux documents. En quoi cela peut-il aider à identifier la nature des échantillons ?
3. On devrait obtenir une répartition en éléments chimiques proche de celle du document 1 [a].
4. On connaît la masse en divers éléments de l'échantillon et sa masse totale. À l'aide d'une relation de proportionnalité, on peut calculer la masse de chaque élément pour une masse totale de 100 mg. On peut ensuite comparer ces valeurs à celles du document 1 pour formuler l'hypothèse.
5. Bien observer l'échelle.
2. Les deux documents apportent le même type d'information : chercher les 3 pourcentages les plus élevés dans chacun des documents, puis indiquer s'ils concernent les mêmes éléments dans les deux documents. En quoi cela peut-il aider à identifier la nature des échantillons ?
3. On devrait obtenir une répartition en éléments chimiques proche de celle du document 1 [a].
4. On connaît la masse en divers éléments de l'échantillon et sa masse totale. À l'aide d'une relation de proportionnalité, on peut calculer la masse de chaque élément pour une masse totale de 100 mg. On peut ensuite comparer ces valeurs à celles du document 1 pour formuler l'hypothèse.
5. Bien observer l'échelle.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
