Mathématiques Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 2
Cours 1
Vecteurs de l'espace
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ATranslation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Soient \text{A} et \text{B} deux points distincts de l'espace. La translation t de vecteur \overrightarrow{\text{AB}} est la transformation qui, à tout point \text{C}, associe l'unique point \text{D} tel que \overrightarrow{\text{CD}} = \overrightarrow{\text{AB}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On étend à l'espace la notion de vecteur étudiée en géométrie plane.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Soient \text{E} et \text{F} deux points de l'espace, \vec{u} un vecteur de l'espace et t la translation de vecteur \vec{u}.
On note \text{E}' et \text{F}' les images respectives de \text{E} et \text{F} par la translation t.
On a alors \overrightarrow{\text{E}'\text{F}'} = \overrightarrow{\text{EF}}.
On note \text{E}' et \text{F}' les images respectives de \text{E} et \text{F} par la translation t.
On a alors \overrightarrow{\text{E}'\text{F}'} = \overrightarrow{\text{EF}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La translation de vecteur \overrightarrow{\text{AB}} associe à tout point \text{C} l'unique point \text{D} tel que \text{[AD]} et \text{[BC]} ont même milieu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
On note t : \text{E} \mapsto \text{E}' la translation de vecteur \vec{u} ; autrement dit t(\text{E}) = \text{E}' \iff \overrightarrow{\text{EE}'} = \vec{u}. De même, t(\text{F}) = \text{F}' \iff \overrightarrow{\text{FF}'} = \vec{u}.
D'après la relation de Chasles, on a \overrightarrow{\text{E}'\text{F}'}= \overrightarrow{\text{E}'\text{E}} + \overrightarrow{\text{EF}} + \overrightarrow{\text{FF}'} soit \overrightarrow{\text{E}'\text{F}'}= - \vec{u} + \overrightarrow{\text{EF}} + \vec{u} = \overrightarrow{\text{EF}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La translation conserve les distances.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
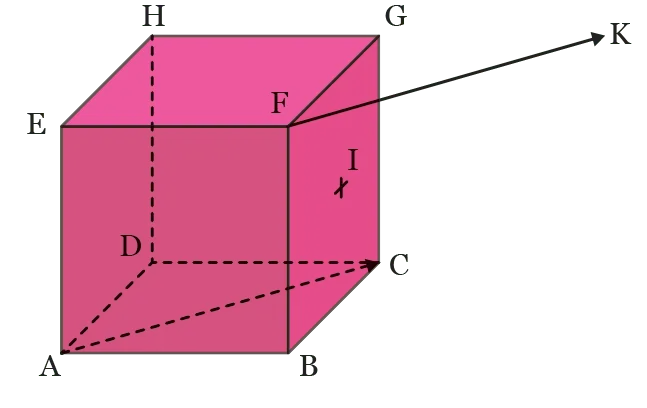
On considère le cube \text{ABCDEFGH} ci-contre.
On note \text{I} le centre du carré \text{BCGF}. Soit t la translation de vecteur \overrightarrow{\text{AC}}. On note \text{K} l'image de \text{F} par t. Montrer que \text{I} est le milieu de [\text{AK}].

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- On traduit vectoriellement les données.
- On utilise les propriétés du parallélogramme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
\text{K} est l'image de \text{F} par t, c'est-à-dire \overrightarrow{\text{FK}} = \overrightarrow{\text{AC}}. Donc \text{ACKF} est un
parallélogramme : ses diagonales se coupent alors en leur milieu. Or,
I est le centre du carré \text{BCGF} donc \text{I} est le milieu de \text{[FC]}. Ainsi, \text{I} est
également le milieu de \text{[AK]}.
Pour s'entraîner
Exercices et p. 72
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BVecteurs colinéaires, vecteurs coplanaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Soient \vec{u} et \vec{v} deux vecteurs de l'espace.
\vec{u} et \vec{v} sont colinéaires lorsqu'il existe un nombre réel \lambda non nul tel que \vec{u} = \lambda \vec{v} ou \vec{v} = \lambda \vec{u}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le vecteur nul est colinéaire à tout vecteur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Soient \text{A}, \text{B} et \text{C} trois points de l'espace deux à deux distincts. Les points \text{A}, \text{B} et \text{C} sont alignés si, et seulement si, les vecteurs \overrightarrow{\text{AB}} et \overrightarrow{\text{AC}} sont colinéaires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Des vecteurs colinéaires non nuls ont la même direction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Les vecteurs \overrightarrow{\text{AB}} et \overrightarrow{\text{AC}} sont colinéaires si, et seulement si, les vecteurs \overrightarrow{\text{AB}} et \overrightarrow{\text{AC}} ont la même direction, c'est-à-dire si, et seulement si, \text{(AB)} et \text{(AC)} sont parallèles. Or, \text{A} appartient à ces deux droites. Elles sont donc confondues, ce qui équivaut à dire que \text{A}, \text{B} et \text{C} sont alignés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
On considère quatre points distincts de l'espace \text{O}, \text{A}, \text{B} et \text{C} et on définit trois vecteurs \vec{u}, \vec{v} et \vec{w} par \vec{u}= \overrightarrow{\text{OA}}, \vec{v}= \overrightarrow{\text{OB}} et \vec{w}= \overrightarrow{\text{OC}}.
On dit que \vec{u}, \vec{v} et \vec{w} sont coplanaires lorsque les points \text{O}, \text{A}, \text{B} et \text{C} appartiennent à un même plan (c'est-à-dire lorsque \text{O}, \text{A}, \text{B} et \text{C} sont coplanaires).
On dit que \vec{u}, \vec{v} et \vec{w} sont coplanaires lorsque les points \text{O}, \text{A}, \text{B} et \text{C} appartiennent à un même plan (c'est-à-dire lorsque \text{O}, \text{A}, \text{B} et \text{C} sont coplanaires).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le vecteur nul est toujours coplanaire à deux autres vecteurs quelconques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Soient \vec{u}, \vec{v} et \vec{w} trois vecteurs de
l'espace tels que \vec{u} et \vec{v} ne sont pas colinéaires (ainsi, \vec{u} et \vec{v} ne sont pas nuls).
Les vecteurs \vec{u}, \vec{v} et \vec{w} sont coplanaires si, et seulement si, il existe deux nombres réels \lambda et \mu tels que \vec{w} = \lambda \vec{u} + \mu \vec{v}.
Les vecteurs \vec{u}, \vec{v} et \vec{w} sont coplanaires si, et seulement si, il existe deux nombres réels \lambda et \mu tels que \vec{w} = \lambda \vec{u} + \mu \vec{v}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On dit que \vec{w} est une combinaison linéaire de \vec{u} et \vec{v}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Cette décomposition est unique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Voir exercice p. 75.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
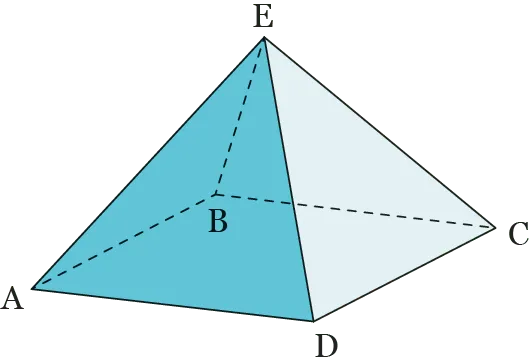
On considère une pyramide \text{ABCDE} de sommet \text{E} dont la base est le parallélogramme \text{ABCD}.
Soient \vec{u} = \overrightarrow{\text{AB}} , \vec{v} = 2 \overrightarrow{\text{AD}} + \overrightarrow{\text{DE}} et \vec{w} = \overrightarrow{\text{AC}} + \overrightarrow{\text{AE}}.
Démontrer que les vecteurs \vec{u}, \vec{v} et \vec{w} sont coplanaires.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour montrer que trois vecteurs \vec{u}, \vec{v} et \vec{w} sont coplanaires, il suffit de déterminer les réels \lambda et \mu tels que \vec{w}=\lambda \vec{u}+\mu \vec{v}.
Pour cela, on décompose le vecteur \vec{w} en utilisant le fait que \text{ABCD} soit un parallélogramme et la relation de Chasles.
Pour cela, on décompose le vecteur \vec{w} en utilisant le fait que \text{ABCD} soit un parallélogramme et la relation de Chasles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
On a \vec{w}=\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AE}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{AE}}.
Or, \text{ABCD} est un parallélogramme donc \overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AD}}.
On a alors \vec{w}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AE}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DE}} soit \vec{w}=\overrightarrow{\mathrm{AB}}+\underbrace{2 \overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DE}}}_{\vec{v}}=\vec{u}+\vec{v} donc les vecteurs sont coplanaires.
Or, \text{ABCD} est un parallélogramme donc \overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AD}}.
On a alors \vec{w}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AE}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DE}} soit \vec{w}=\overrightarrow{\mathrm{AB}}+\underbrace{2 \overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DE}}}_{\vec{v}}=\vec{u}+\vec{v} donc les vecteurs sont coplanaires.
Pour s'entraîner
Exercices et p. 72
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CVecteurs linéairement indépendants et base de l'espace
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Soient \vec{u}, \vec{v} et \vec{w} trois vecteurs de l'espace et a, b et c trois réels.
Les vecteurs \vec{u}, \vec{v} et \vec{w} sont dits linéairement indépendants lorsqu'ils ne sont pas coplanaires, autrement dit lorsque a \vec{u} + b \vec{v} + c \vec{w} = 0 \Rightarrow a = b = c = 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Deux vecteurs non colinéaires sont linéairement indépendants.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Trois vecteurs linéairement indépendants forment une base de l'espace.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On note ( \vec{i} \ , \ \vec{j} \ , \ \vec{k}) une base de l'espace.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Soit ( \vec{i} \ , \ \vec{j} \ , \ \vec{k}) une base de l'espace.
Pour tout vecteur \vec{w} de l'espace, il existe un unique triplet de réels (x \ ; \ y \ ; \ z) tel que \vec{w} = x \vec{i} + y \vec{j} + z \vec{k} . Cette décomposition est donc unique.
Pour tout vecteur \vec{w} de l'espace, il existe un unique triplet de réels (x \ ; \ y \ ; \ z) tel que \vec{w} = x \vec{i} + y \vec{j} + z \vec{k} . Cette décomposition est donc unique.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right) sont les coordonnées de \vec{w} dans la base ( \vec{i} \ , \ \vec{j} \ , \ \vec{k}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Soient \vec{w} un vecteur de l'espace, \text{O} un point de l'espace et \text{M} le point tel que \vec{w} = \overrightarrow{\text{OM}}.
On note \text{M}' le projeté de \text{M} sur le plan de repère (\text{O} \ ; \ \vec{i} \ , \ \vec{j} ) parallèlement à l'axe (\text{O}z).
On a \overrightarrow{\mathrm{OM}}=\overrightarrow{\mathrm{OM}'}+\overrightarrow{\mathrm{M}' \mathrm{M}} . Or \overrightarrow{\text{M}'\text{M}} et \vec{k} sont colinéaires donc il existe un unique réel z tel que \overrightarrow{\text{M'M}} = z \vec{k}. De plus, \overrightarrow{\text{OM}'}, \vec{i} et \vec{j} sont coplanaires donc il existe deux réels x et y uniques tels que \overrightarrow{\mathrm{OM}'}=x \vec{i} +y \vec{j}. On a ainsi \overrightarrow{\mathrm{OM}}=\overrightarrow{\mathrm{OM}'}+\overrightarrow{\mathrm{M}" \mathrm{M}}=x \vec{i}+y \vec{j}+z \vec{k}, soit \vec{w} = x \vec{i} + y \vec{j} + z \vec{k}.
On a \overrightarrow{\mathrm{OM}}=\overrightarrow{\mathrm{OM}'}+\overrightarrow{\mathrm{M}' \mathrm{M}} . Or \overrightarrow{\text{M}'\text{M}} et \vec{k} sont colinéaires donc il existe un unique réel z tel que \overrightarrow{\text{M'M}} = z \vec{k}. De plus, \overrightarrow{\text{OM}'}, \vec{i} et \vec{j} sont coplanaires donc il existe deux réels x et y uniques tels que \overrightarrow{\mathrm{OM}'}=x \vec{i} +y \vec{j}. On a ainsi \overrightarrow{\mathrm{OM}}=\overrightarrow{\mathrm{OM}'}+\overrightarrow{\mathrm{M}" \mathrm{M}}=x \vec{i}+y \vec{j}+z \vec{k}, soit \vec{w} = x \vec{i} + y \vec{j} + z \vec{k}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La méthode vue dans l'application précédente se généralise. Pour démontrer qu'un nombre quelconque de vecteurs ne sont pas linéairement indépendants, il suffit de montrer que l'un d'eux est une combinaison linéaire des autres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Dans la base ( \vec{i} \ , \ \vec{j} \ , \ \vec{k}), on donne les vecteurs \vec{u} = \vec{i} + \vec{j} + \vec{k} , \vec{v} = - \vec{i} + \vec{j} et \vec{w} = \vec{i} + \vec{k}.
Déterminer les coordonnées des vecteurs \vec{u}, \vec{v} et \vec{w} puis montrer qu'ils sont linéairement indépendants.
Que peut-on en déduire ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Chacun des vecteurs est écrit en fonction de \vec{i}, \vec{j} et \vec{k} : on détermine donc directement leurs coordonnées en analysant les coefficients.
- Pour montrer que les vecteurs sont linéairement indépendants, on résout le système associé à l'équation vectorielle a \vec{u}+b \vec{v}+c \vec{w}=\overrightarrow{0} : on doit obtenir a=b=c=0.
- Les vecteurs étant linéairement indépendants, ils forment une base de l'espace.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
On a \vec{u}=\left(\begin{array}{l}
1 \\
1 \\
1
\end{array}\right), \vec{v}=\left(\begin{array}{c}
-1 \\
1 \\
0
\end{array}\right) et \vec{w}=\left(\begin{array}{l}
1 \\
0 \\
1
\end{array}\right).
Supposons qu'il existe trois réels a, b et c tels que a \overrightarrow{u}+b \overrightarrow{v}+c \overrightarrow{w}=\overrightarrow{0}.
Montrons que a=b=c=0.
En effet, a \overrightarrow{u}+b \overrightarrow{v}+c \overrightarrow{w}=\overrightarrow{0} \Leftrightarrow\left\{\begin{array} { c } { a - b + c = 0 } \\ { a + b = 0 } \\ { a + c = 0 } \end{array} \Leftrightarrow \left\{\begin{array}{l} a=0 \\ b=0 \\ c=0 \end{array}\right.\right..
Les vecteurs \vec{u}, \vec{v} et \vec{w} sont linéairement indépendants. Ils forment donc une base de l'espace.
Supposons qu'il existe trois réels a, b et c tels que a \overrightarrow{u}+b \overrightarrow{v}+c \overrightarrow{w}=\overrightarrow{0}.
Montrons que a=b=c=0.
En effet, a \overrightarrow{u}+b \overrightarrow{v}+c \overrightarrow{w}=\overrightarrow{0} \Leftrightarrow\left\{\begin{array} { c } { a - b + c = 0 } \\ { a + b = 0 } \\ { a + c = 0 } \end{array} \Leftrightarrow \left\{\begin{array}{l} a=0 \\ b=0 \\ c=0 \end{array}\right.\right..
Les vecteurs \vec{u}, \vec{v} et \vec{w} sont linéairement indépendants. Ils forment donc une base de l'espace.
Pour s'entraîner
Exercices p. 72 et p. 73
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
