1

Distance entre un point de l’espace et une droite

Dans GeoGebra, ouvrir une fenêtre 3D et n’afficher ni le plan, ni les axes.

1. En utilisant la barre de saisie, placer les points $\text{K}$ et $\text{L}$ à l’aide de leurs coordonnées.

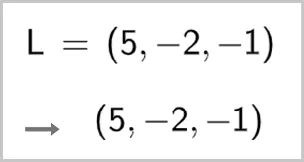
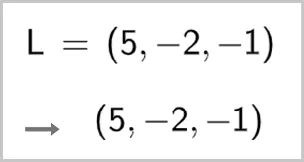
2. Créer un vecteur directeur $\overrightarrow{u}$ de la droite $\Delta$ dans la barre de saisie.

3. Créer un représentant du vecteur $\overrightarrow{u}$ ayant pour origine $\text{K}$ pour ensuite tracer la droite $\Delta$.

4. Placer un point $\text{M}$ sur cette droite et faire afficher la longueur $\text{LM}$.

5. Déplacer le point $\text{M}$ jusqu’à obtenir la longueur minimale de $\text{LM}$.
Quelles sont alors les coordonnées de $\text{M}$?

6. Affcher la mesure de l’angle $\widehat{\text{LMK}}$.
Que constate-t-on ?

Lancer le module Geogebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

On considère le code Python ci-dessous.

1. Que renvoie la fonction droite ? Faire un essai avec $t=2$.
2. Que renvoie la fonction distance ? Faire un essai en prenant comme argument droite(2).
3. Créer une fonction test qui prend en entrée $t_1$ et $t_2$ correspondant à deux points $\text{A}$ et $\text{B}$ de la droite $\Delta$ et un pas $p$ et qui renvoie la distance minimale entre le point $\text{L}$ et les points du segment $[\text{AB}]$.



4. Utiliser cette fonction pour déterminer le point de $\Delta$ le plus proche de $\text{L}$ lorsque $t\in [-5;5]$ avec un pas de $1$, puis un pas de $0,1$.

from math import sqrt
def droite(t) :
	x = 4*t - 3
	y = 2*t
	z = 4*t - 1
	return([x, y, z])

def distance(l) :
	d = sqrt((l[0]-5)**2+(l[1]+2)**2+(l[2]+1)**2)
	return(d)

Ouvrir une feuille de calcul.

1. Dans la colonne A, placer les valeurs de $t$ de $-5$ à $5$ avec un incrément de $1$.
2. Dans les colonnes B, C et D, calculer les coordonnées $x$, $y$ et $z$ des points de la droite $\Delta$ correspondant aux valeurs de $t$ de la colonne A.
3. Dans la colonne E, calculer la distance de chaque point à $\text{L}$ en utilisant la formule adéquate.

4. Quelles semblent être les coordonnées du point le plus proche de $\text{L}$ ?

5. Refaire les mêmes manipulations avec un pas de $0,1$ pour les valeurs de $t$, puis avec un pas de $0,01$.