Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 3
TP INFO
Intersection d'un plan et d'un cube
13 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On considère le cube \text{ABCDEFGH} de côté 2 ci-contre.
On donne \overrightarrow{i}=\frac{1}{2} \overrightarrow{\mathrm{AB}}, \overrightarrow{j}=\frac{1}{2} \overrightarrow{\mathrm{AD}} et \overrightarrow{k}=\frac{1}{2} \overrightarrow{\mathrm{AE}}.
On défnit les points \text{L} tel que \overrightarrow{\mathrm{FL}}=\frac{1}{4} \overrightarrow{\mathrm{FG}} et \text{K} tel que \overrightarrow{\mathrm{GK}}=\frac{1}{4} \overrightarrow{\mathrm{GH}}.
Le point \text{M} est un point du segment [\text{CG}].
On a \overrightarrow{\mathrm{CM}}=t \times \overrightarrow{k} avec t \in[0 \,; 2].
Questions préliminaires :
1.Justifer que (\mathrm{A} \: ; \overrightarrow{i} \: , \overrightarrow{j} \: , \overrightarrow{k}) est un repère orthonormé de l'espace.
2. Dans le repère (\mathrm{A} \: ; \overrightarrow{i} \: , \overrightarrow{j} \: , \overrightarrow{k}), donner les coordonnées de tous les points de la figure ci-contre.
3. Donner, dans ce repère, les coordonnées des vecteurs \overrightarrow{\mathrm{ML}} et \overrightarrow{\mathrm{MK}}.
4. Calculer \text {ML}, \text {MK} et \overrightarrow{\mathrm{ML}} \cdot \overrightarrow{\mathrm{MK}}.
On défnit les points \text{L} tel que \overrightarrow{\mathrm{FL}}=\frac{1}{4} \overrightarrow{\mathrm{FG}} et \text{K} tel que \overrightarrow{\mathrm{GK}}=\frac{1}{4} \overrightarrow{\mathrm{GH}}.
Le point \text{M} est un point du segment [\text{CG}].
On a \overrightarrow{\mathrm{CM}}=t \times \overrightarrow{k} avec t \in[0 \,; 2].
Questions préliminaires :
1.Justifer que (\mathrm{A} \: ; \overrightarrow{i} \: , \overrightarrow{j} \: , \overrightarrow{k}) est un repère orthonormé de l'espace.
2. Dans le repère (\mathrm{A} \: ; \overrightarrow{i} \: , \overrightarrow{j} \: , \overrightarrow{k}), donner les coordonnées de tous les points de la figure ci-contre.
3. Donner, dans ce repère, les coordonnées des vecteurs \overrightarrow{\mathrm{ML}} et \overrightarrow{\mathrm{MK}}.
4. Calculer \text {ML}, \text {MK} et \overrightarrow{\mathrm{ML}} \cdot \overrightarrow{\mathrm{MK}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Trouver une position approchée du point \text{M} tel que la mesure de l'angle \widehat{\text{LMK}} soit 45^\circ à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
1. Placer les deux points \text{A} et \text{B} en utilisant leurs coordonnées.
2. Avec l'outil Cube, faire apparaître le cube \text{ABCDEFGH}.
3. Dans la barre de saisie, créer les points \text{L} et \text{K}.
4. Placer un point \text{M} mobile sur le segment [\text{CG}].
5. Faire apparaître une mesure de l'angle \widehat{\text{LMK}}.
2. Avec l'outil Cube, faire apparaître le cube \text{ABCDEFGH}.
Le zoom est accessible dans la version Premium.
3. Dans la barre de saisie, créer les points \text{L} et \text{K}.
4. Placer un point \text{M} mobile sur le segment [\text{CG}].
5. Faire apparaître une mesure de l'angle \widehat{\text{LMK}}.
6. Déplacer le point \text{M} de façon à ce que l'angle \widehat{\text{LMK}} ait une mesure la plus proche possible de 45^\circ.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
Ouvrir une feuille de calcul. (Fichier téléchargeable ).
1. Dans la colonne A, mettre les valeurs possibles pour t, avec un pas de 0{,}1.
2. Dans les colonnes B et C, calculer le carré des longueurs \text{ML} et \text{MK}.
3. Dans la colonne D calculer le produit scalaire \overrightarrow{\mathrm{ML}} \cdot \overrightarrow{\mathrm{MK}}.
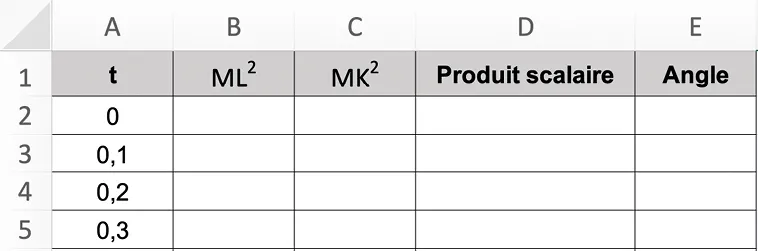
2. Dans les colonnes B et C, calculer le carré des longueurs \text{ML} et \text{MK}.
3. Dans la colonne D calculer le produit scalaire \overrightarrow{\mathrm{ML}} \cdot \overrightarrow{\mathrm{MK}}.
Le zoom est accessible dans la version Premium.
4. En utilisant la fonction ACOS(), calculer une valeur approchée de la mesure de l'angle.
Attention : cette mesure est exprimée en radian, il faut la convertir en degré.
5. Trouver la valeur de t telle que l'angle \widehat{\text{LMK}} ait une mesure la plus proche possible de 45^\circ.
6. Recommencer avec un pas de 0{,}01.
Attention : cette mesure est exprimée en radian, il faut la convertir en degré.
Le zoom est accessible dans la version Premium.
5. Trouver la valeur de t telle que l'angle \widehat{\text{LMK}} ait une mesure la plus proche possible de 45^\circ.
6. Recommencer avec un pas de 0{,}01.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer une mesure de l'angle \widehat{\text{FMG}} lorsque \text{M} est le centre du cube \text{ABCDEFGH}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah