Physique-Chimie Terminale Spécialité
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 5
Exercice corrigé
Âge de la Terre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Compétence(s)
APP : Faire des prévision à l'aide d'un modèle
VAL : Analyser des résultats
VAL : Analyser des résultats
La datation à l'uranium-plomb permet de déterminer assez précisément l'âge de la Terre, le plomb étant le produit final stable de la désintégration de l'uranium 238. Si l'on mesure la quantité de plomb 206 dans un échantillon de roche, en considérant qu'il n'y en avait pas initialement, on peut déterminer l'âge du minéral.
On s'intéresse à un échantillon de roche dont l'âge correspond à celui de la Terre. La courbe de décroissance radioactive théorique de cette roche est fournie dans le . Le nombre de noyaux de plomb mesuré dans la roche à la date t_{\text{Terre}}, noté N_{\text{Pb}}(t_{\text{Terre}}), est égal à 2{,}5 \times 10^{12}.
On s'intéresse à un échantillon de roche dont l'âge correspond à celui de la Terre. La courbe de décroissance radioactive théorique de cette roche est fournie dans le . Le nombre de noyaux de plomb mesuré dans la roche à la date t_{\text{Terre}}, noté N_{\text{Pb}}(t_{\text{Terre}}), est égal à 2{,}5 \times 10^{12}.
1. Indiquer le nombre initial N_\text{U}(t_0) de noyaux d'uranium.
2. Définir et déterminer graphiquement le temps de demi-vie t_{1/2}.
3. Exprimer le nombre de noyaux d'uranium 238 au cours du temps.
2. Définir et déterminer graphiquement le temps de demi-vie t_{1/2}.
3. Exprimer le nombre de noyaux d'uranium 238 au cours du temps.
4. . Établir la relation entre le nombre de noyaux d'uranium 238 au
moment de la formation de la roche, N_\text{U}(t_0), N_\text{U}(t_\text{Terre}) et N_\text{Pb}(t_\text{Terre}).
5. Calculer le nombre N_\text{U}(t_\text{Terre}) de noyaux d'uranium et déterminer l'âge de la Terre.
5. Calculer le nombre N_\text{U}(t_\text{Terre}) de noyaux d'uranium et déterminer l'âge de la Terre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Dérive des continents
Sur des temps géologiques de l'ordre du dixième du temps de demi-vie de l'uranium 238, la surface de la Terre a beaucoup évolué.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
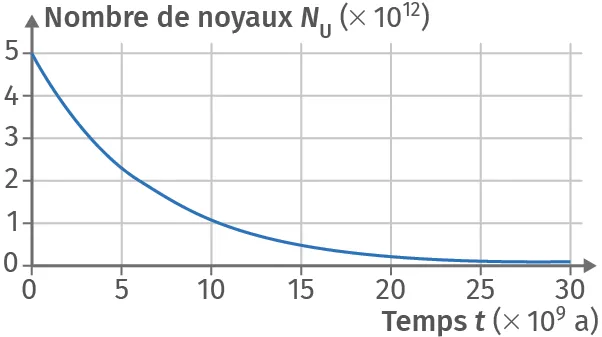
Doc. 2Courbe de décroissance radioactive
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution rédigée
1. Par lecture graphique, N_{\text{U}}(t_0) = 5{,}0 \times 10^{12} noyaux.
2. Le temps de demi-vie t_{1/2} est la durée au bout de laquelle la moitié des noyaux d'un échantillon se sont désintégrés. Ici, on trouve pour N_{\text{U}}(t_{1/2}) = \dfrac{N_{\text{U}}(t_0)}{2} un temps de demi-vie t_{1/2} = 4{,}5 \times 10^9 a.
3. On sait que la population d'un échantillon de noyaux radioactifs évolue selon la loi de décroissance radioactive :
4. En considérant qu'il n'y a pas de noyaux de plomb initialement présents dans la roche, on a la relation :
5. AN : N_{\text{U}} (t_{\text{Terre}}) = 5{,}0 \times 10^{12} - 2{,}5 \times 10^{12} = 2{,}5 \times 10^{12}
En utilisant la loi de décroissance, on trouve :
2. Le temps de demi-vie t_{1/2} est la durée au bout de laquelle la moitié des noyaux d'un échantillon se sont désintégrés. Ici, on trouve pour N_{\text{U}}(t_{1/2}) = \dfrac{N_{\text{U}}(t_0)}{2} un temps de demi-vie t_{1/2} = 4{,}5 \times 10^9 a.
3. On sait que la population d'un échantillon de noyaux radioactifs évolue selon la loi de décroissance radioactive :
N_\text{U}(t) = N_\text{U}(t_0) \cdot \text{exp}(-\lambda \cdot t) avec \lambda = \dfrac{\ln(2)}{t_{1/2}}
4. En considérant qu'il n'y a pas de noyaux de plomb initialement présents dans la roche, on a la relation :
N_{\text{U}} (t_{\text{Terre}}) = N_{\text{U}}(t_0) - N_{\text{Pb}} (t_{\text{Terre}})
5. AN : N_{\text{U}} (t_{\text{Terre}}) = 5{,}0 \times 10^{12} - 2{,}5 \times 10^{12} = 2{,}5 \times 10^{12}
En utilisant la loi de décroissance, on trouve :
t_{\text{Terre}} = \dfrac{\ln \bigg( \dfrac{N_{\text{U}}(t_0)}{N_{\text{U}}(t_{\text{Terre}})} \bigg)}{\ln(2)} \cdot t_{1/2}
AN : t_{\text{Terre}} = \dfrac{\ln \bigg( \dfrac{5{,}0 \times 10^{12}}{2{,}5 \times 10^{12}} \bigg)}{\ln(2)} \times 4{,}5 \times 10^9 a
AN : t_{\text{Terre}} = \dfrac{\ln \bigg( \dfrac{5{,}0 \times 10^{12}}{2{,}5 \times 10^{12}} \bigg)}{\ln(2)} \times 4{,}5 \times 10^9 a
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Protocole de réponse
1. Identifier sur le graphe la quantité N_\text{U} à t_0 = 0 s.
2. Rappeler la définition du temps de demi-vie. Faire une lecture graphique en abscisse du temps pour lequel la quantité N_\text{U} est égale à \dfrac{N_{\text{U}}(t_0)}{2}.
3. Restituer la formule en l'adaptant aux notations de l'énoncé.
4. Identifier chaque grandeur physique. Exprimer la relation en respectant la conservation du nombre de noyaux.
5. Restituer une formule du cours. Remplacer chaque terme en utilisant les unités adéquates pour chaque grandeur physique.
2. Rappeler la définition du temps de demi-vie. Faire une lecture graphique en abscisse du temps pour lequel la quantité N_\text{U} est égale à \dfrac{N_{\text{U}}(t_0)}{2}.
3. Restituer la formule en l'adaptant aux notations de l'énoncé.
4. Identifier chaque grandeur physique. Exprimer la relation en respectant la conservation du nombre de noyaux.
5. Restituer une formule du cours. Remplacer chaque terme en utilisant les unités adéquates pour chaque grandeur physique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Mise en application
Découvrez l', Ôtzi, pour travailler cette notion.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
