Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Thème 4
Sujet Bac guidé 2
Lunette astronomique
Téléchargez ce sujet en format pdf .
Ce document est actuellement projeté sur le côté de votre écran.
Énoncé
La lunette a été inventée en Europe à la fin du XVIe siècle. Elle a connu un rapide succès en étant utilisée comme longue‑vue. En 1609, Galilée fut le premier scientifique à utiliser la lunette pour observer le ciel. Il construisit et perfectionna ses propres lunettes, ce qui lui permit de faire de nombreuses découvertes comme quatre des satellites de Jupiter ainsi que la rotation du Soleil sur lui‑même.
Ce document est actuellement projeté sur le côté de votre écran.
Doc. 1 Composants de la lunette astronomique
Le zoom est accessible dans la version Premium.
Crédits : Internet Archive Book Images/Flickr
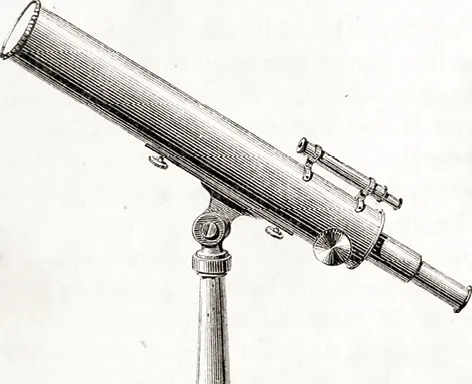
La lunette astronomique se compose d'un objectif de grande distance focale, qui crée une image intermédiaire des objets lointains, et d'un oculaire de courte distance focale qui renvoie une image à l'infini.
Le doc. 3 présente le schéma optique d'une telle lunette où l'objectif et l'oculaire sont modélisés par deux lentilles minces et .
La lunette est dite afocale : le foyer image de l'objectif est confondu avec le foyer objet de l'oculaire, de sorte que l'image d'un objet à l'infini se situe également à l'infini.
Le doc. 3 présente le schéma optique d'une telle lunette où l'objectif et l'oculaire sont modélisés par deux lentilles minces et .
La lunette est dite afocale : le foyer image de l'objectif est confondu avec le foyer objet de l'oculaire, de sorte que l'image d'un objet à l'infini se situe également à l'infini.
Ce document est actuellement projeté sur le côté de votre écran.
Doc. 2 Vergence d'une lentille
La vergence d'une lentille, usuellement notée , est définie par :
: vergence ()
: distance focale (m)
: distance focale (m)
Ce document est actuellement projeté sur le côté de votre écran.
Doc. 3 Schéma optique d'une lunette astronomique
Le zoom est accessible dans la version Premium.
Crédits : Lelivrescolaire.fr
Le schéma optique ci-dessus représente une lunette astronomique avec deux rayons incidents provenant d'un objet lointain . On ne considère que les rayons parallèles provenant de , faisant un angle avec l'axe optique.
Ce document est actuellement projeté sur le côté de votre écran.
Données
- Distance focale de l'objectif : cm
- Vergence de l'oculaire :
Ce document est actuellement projeté sur le côté de votre écran.
Coups de pouce
1.1 Utiliser la relation entre vergence et
distance focale.
1.2 Comparer les distances focales.
1.3 Tenir compte de la position de l'image intermédiaire.
1.4 Tracer les rayons en tenant compte des règles de construction géométrique.
1.2 Comparer les distances focales.
1.3 Tenir compte de la position de l'image intermédiaire.
1.4 Tracer les rayons en tenant compte des règles de construction géométrique.
Ce document est actuellement projeté sur le côté de votre écran.
Questions
1
Éléments de la lunette
1.1 Calculer la distance focale de l'oculaire.
1.2 Justifier que et sont respectivement l'objectif et l'oculaire.
2
Position de l'image intermédiaire
L'extrémité d'un objet lointain émet des rayons parallèles faisant un angle avec l'axe optique. L'objectif forme une image intermédiaire de cet objet.
2.1 Justifier que l'oculaire donne une image située à l'infini.
2.2 Zoomer sur l'image et cliquer sur le pinceau pour afficher l'outil de dessin pour pouvoir modifier le schéma. Représenter le trajet des deux rayons lumineux. Faire figurer sur le schéma.
Le zoom est accessible dans la version Premium.
Crédits : Lelivrescolaire.fr
Ce document est actuellement projeté sur le côté de votre écran.
Doc. 4 Influence d'une ouverture
Le zoom est accessible dans la version Premium.
Crédits : Lelivrescolaire.fr
: diamètre de l'ouverture (m)
: longueur d'onde (m)
: écart angulaire (rad)
: longueur d'onde (m)
: écart angulaire (rad)
Ce document est actuellement projeté sur le côté de votre écran.
Doc. 5 Critère de Rayleigh
Le critère de Rayleigh permet d'évaluer la capacité d'un instrument optique à discerner les détails. Il stipule que deux objets sont discernables si l'écart angulaire qui les sépare est supérieur à l'écart angulaire de la tache d'Airy formée par le système optique.
Tache de gauche :
Tache au centre :
Tache de droite :
Le zoom est accessible dans la version Premium.
Crédits : Ellande/Wikimedia
Tache de gauche :
Tache au centre :
Tache de droite :
Ce document est actuellement projeté sur le côté de votre écran.
Données
- Diamètre de l'objectif : cm
- Longueur d'onde à considérer : nm
Ce document est actuellement projeté sur le côté de votre écran.
Coups de pouce
3.1. Il s'agit de l'un des phénomènes caractéristiques des ondes.
3.2 Utiliser le critère de Rayleigh.
3.2 Utiliser le critère de Rayleigh.
Ce document est actuellement projeté sur le côté de votre écran.
Questions
L'image intermédiaire d'un point par l'objectif est une tache et non un point, ce qui limite la résolution de la lunette astronomique.
3.1 Nommer le phénomène mis en jeu.
3.2 Calculer l'écart angulaire minimal séparant deux points pour que l'on puisse les distinguer.
3
Résolution de la lunette
3.1 Nommer le phénomène mis en jeu.
3.2 Calculer l'écart angulaire minimal séparant deux points pour que l'on puisse les distinguer.
Ce document est actuellement projeté sur le côté de votre écran.
Doc. 6 Grossissement
Le zoom est accessible dans la version Premium.
Crédits : Lelivrescolaire.fr
Dans le cas de petits angles exprimés en radian (rad), on peut faire l'approximation :
Ce document est actuellement projeté sur le côté de votre écran.
Données
- Angle limite de l'observation de l'œil humain moyen : rad
- Distance Terre‑Lune : m
Ce document est actuellement projeté sur le côté de votre écran.
Coups de pouce
4.1. Utiliser une relation trigonométrique
dans le triangle , puis dans le
triangle ainsi que l'approximation
des petits angles.
4.2 Estimer la taille du drapeau et calculer l'angle d'observation à l'œil nu. Déterminer l'angle d'observation à travers la lunette et conclure.
4.2 Estimer la taille du drapeau et calculer l'angle d'observation à l'œil nu. Déterminer l'angle d'observation à travers la lunette et conclure.
Ce document est actuellement projeté sur le côté de votre écran.
Questions
4
Grossissement de la lunette
4.1 Exprimer le grossissement en fonction de et .
4.2 Toute trace de recherche, même incomplète, ou d'initiatives, même infructueuses, serait prise en compte à l'examen.
En observant la Lune depuis la Terre avec cette lunette, évaluer la possibilité de distinguer le drapeau américain posé en 1969.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarahUtilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.
