Physique-Chimie Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 14
Exercices
Pour s'entraîner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22Couronne de Hiéron
✔ Couronne de Hiéron

Le roi Hiéron II de Syracuse n'est pas sûr de l'honnêteté de son joaillier. Il lui a donné deux mines (une unité antique dont la valeur exacte est aujourd'hui inconnue) d'or pour qu'il réalise une couronne, celui‑ci lui a bien fabriqué une couronne de deux mines, mais le roi a un doute. Le joaillier n'aurait‑il pas gardé de l'or pour lui qu'il aurait remplacé par de l'argent, moins cher ? Il demande de l'aide à Archimède. Celui‑ci mesure la masse m_{1} de la couronne et trouve bien une masse correspondant à deux mines. Lorsqu'il plonge la couronne dans l'eau, il doit ajouter du côté de la couronne une masse m_{2}=\frac{m_{1}}{15} pour avoir une balance à l'équilibre. Il fait de même pour un petit morceau d'or de masse m_{1}^{\prime} et trouve m_{2}^{\prime}=\frac{m_{1}^{\prime}}{19}.
1. Réaliser un bilan des forces sur la couronne.
2. Calculer la densité de la couronne.
3. Calculer la densité de l'or.
4. Rechercher la densité de l'argent sur Internet.
5. Conclure sur l'authenticité de la couronne.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23Rebond post-glaciaire
✔ RAI/ANA : Construire un raisonnement
Sur Terre, certaines régions ont un sol qui remonte à une vitesse d'environ 5 mm par an. Celles‑ci ont toutes pour point commun d'avoir été recouvertes par une calotte glaciaire durant la dernière glaciation. Cette calotte, d'épaisseur e = 3 km et de densité d = 0{,}9, a depuis disparu. La croûte continentale a une épaisseur supposée homogène de 35 km et une masse volumique \rho_{\text {croûte }}=2{,}699 g·cm-3 et flotte sur le manteau de masse volumique \rho_{\text {manteau }} = 3\,270 kg·m-3.
1. Calculer la hauteur de la croûte par rapport à la surface du manteau, en raisonnant sur une surface de 1 km2.
2. En ajoutant une épaisseur e de glace au sommet de la croûte continentale, calculer l'enfoncement de la croûte.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24Masse volumique du bois
✔ RAI/ANA : Élaborer un protocole


On souhaite mesurer la masse volumique d'une statue en genévrier, un bois dont la masse volumique est d'environ 560 kg·m-3.
1. Justifier que la méthode proposée dans l'exercice corrigé Densités des alliages métalliques ne permet pas de mesurer la densité d'objets moins dense que l'eau.
2. Proposer une méthode pour déterminer la masse volumique d'objets moins denses que l'eau.
2. Proposer une méthode pour déterminer la masse volumique d'objets moins denses que l'eau.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Vélocimètre Venturi
✔ APP : Extraire l'information utile
Afin de mesurer la vitesse de l'air le long d'une
conduite, un resserrement de section S_{1} \lt S_{0} est couplé
à un manomètre à mercure, comme indiqué sur
le schéma.


1. À l'aide de la loi fondamentale de l'hydrostatique,
relier \Delta h, p_{1}, p_{0} g et \rho_{\mathrm{Hg}}.
2. Exprimer v_{0} en fonction de \Delta h, \frac{S_{0}}{S_{1}}, g, \rho_{\mathrm{Hg}} et \rho_{\text {air}}.
2. Exprimer v_{0} en fonction de \Delta h, \frac{S_{0}}{S_{1}}, g, \rho_{\mathrm{Hg}} et \rho_{\text {air}}.
3. Calculer v_{0} pour \Delta h=3 cm, S_{0} = 3 \;S_{1} en
recherchant les données manquantes sur Internet.
Détails du barème
Détails du barème TOTAL / 5 pts
1 pt
1. Donner la loi fondamentale de l'hydrostatique.1 pt
1. Calculer \Delta h.0,5 pt
2. Utiliser la conservation du débit volumique.1 pt
2. Écrire la formule de Bernoulli.1 pt
2. Calculer v_{0}.0,5 pt
3. Effectuer l'application numérique.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Torrents et fleuves
✔ VAL : Analyser des résultats


Soit une rivière de largeur L uniforme et de hauteur h(x). La vitesse est v(x) et ne dépend que de x. On note v_{0} et h_{0} la vitesse et la hauteur à l'abscisse x = 0 m. La pression à la surface vaut partout p_{0}.
1. Écrire la loi de
conservation du débit volumique D_{\mathrm{v}} et relier en tout
point v(x), h(x), v_{0} et h_{0}.
2. En appliquant la loi de Bernoulli, montrer que l'on peut écrire :
3. Déterminer l'expression de a en fonction de L, h_{0} et v_{0}.
2. En appliquant la loi de Bernoulli, montrer que l'on peut écrire :
D_{V}=a \cdot Z \cdot \sqrt{1-Z} avec Z=\dfrac{2 g \cdot h(x)}{v_{0}^{2}+2 g \cdot h_{0}}
3. Déterminer l'expression de a en fonction de L, h_{0} et v_{0}.
4. À l'aide de la représentation graphique de la fonction f(Z)=Z · \sqrt{1-Z}, montrer que pour une valeur de
débit donnée, il existe deux valeurs possibles de
hauteur d'eau.
5. Ces solutions sont appelées « hauteur fleuve » et « hauteur torrent ». En comparant les valeurs de vitesse et de hauteur d'eau, justifier ces noms.
5. Ces solutions sont appelées « hauteur fleuve » et « hauteur torrent ». En comparant les valeurs de vitesse et de hauteur d'eau, justifier ces noms.
Doc. 1
Représentation schématique de la rivière

Doc. 2
Courbe représentative de la fonction \boldsymbol{Z} \cdot \sqrt{\bf{1 - \boldsymbol{Z}}}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Copie d'élève à commenter
Proposer une justification pour chaque erreur relevée par le correcteur.
Un château d'eau contient un réservoir d'eau de section S = 100 m2, dont la surface est à l'altitude z_{2} = 45 m.
Léa ouvre un robinet à l'altitude z_{1} = 10 m, dont l'ouverture a pour section s = 1 cm2.
Données
- Masse volumique de l'eau : \rho=0{,}99 g·cm-3
- Intensité de pesanteur : g = 9{,}81 N·kg-1
- Pression atmosphérique : p_{0}=1~013 hPa
1. Réaliser un schéma du château d'eau, du robinet et de la canalisation les reliant.

2. Calculer la pression p au niveau du robinet en l'absence d'écoulement.
Quand l'eau ne coule pas, on peut
appliquer la relation de la statique des
fluides : \color{red}\cancel{\color{black}{\Delta p=g · \Delta z}}
La pression en haut du château d'eau est la pression atmosphérique :
\begin{array}{l} p=p_{0}+\rho \cdot g \cdot \left(z_{2}-z_{1}\right) \\ p=1~013 \times 10^{2}+\color{red}\cancel{\color{black}0{,}99}\color{black} \times 9,81 \times(45-10) \\ p=\color{red}\cancel{\color{black}{1~016 \;\mathrm{hPa}}} \end{array}
La pression en haut du château d'eau est la pression atmosphérique :
\begin{array}{l} p=p_{0}+\rho \cdot g \cdot \left(z_{2}-z_{1}\right) \\ p=1~013 \times 10^{2}+\color{red}\cancel{\color{black}0{,}99}\color{black} \times 9,81 \times(45-10) \\ p=\color{red}\cancel{\color{black}{1~016 \;\mathrm{hPa}}} \end{array}
3. Exprimer la vitesse v_{1} de l'eau en sortie du robinet.
La pression à la surface de l'eau du château d'eau et au robinet est la pression atmosphérique p_{0}. La
conservation du débit volumique permet
d'écrire que D_{v}=S \cdot v_{2}^{2}=s \cdot v_{1}^{2}. D'après
la loi de Bernoulli :
\begin{array}{l} \rho \cdot \frac{v_{1}^{2}}{2}+\rho \cdot g \cdot z_{1}+p_{0}=\rho \cdot \frac{v_{2}^{2}}{2}+\rho \cdot g \cdot z_{2}+p_{0} \\ \frac{v_{1}^{2}}{2}+g \cdot z_{1}=\dfrac{v_{2}^{2}}{2}+g \cdot z_{2} \\ \frac{v_{1}^{2}}{2}+g \cdot z_{1}=\dfrac{v_{1}^{2} \cdot s^{2}}{2 S^{2}}+g \cdot z_{2} \\ \frac{v_{1}^{2}}{2} \cdot\left(1-\frac{s^{2}}{S^{2}}\right)= g \cdot\left(z_{2}-z_{1}\right) \\ \color{red}\cancel{\color{black}{v_{1}=\frac{2 g \cdot\left(z_{2}-z_1 \right) \cdot s^{2}}{S^{2}-s^{2}}}} \end{array}
\begin{array}{l} \rho \cdot \frac{v_{1}^{2}}{2}+\rho \cdot g \cdot z_{1}+p_{0}=\rho \cdot \frac{v_{2}^{2}}{2}+\rho \cdot g \cdot z_{2}+p_{0} \\ \frac{v_{1}^{2}}{2}+g \cdot z_{1}=\dfrac{v_{2}^{2}}{2}+g \cdot z_{2} \\ \frac{v_{1}^{2}}{2}+g \cdot z_{1}=\dfrac{v_{1}^{2} \cdot s^{2}}{2 S^{2}}+g \cdot z_{2} \\ \frac{v_{1}^{2}}{2} \cdot\left(1-\frac{s^{2}}{S^{2}}\right)= g \cdot\left(z_{2}-z_{1}\right) \\ \color{red}\cancel{\color{black}{v_{1}=\frac{2 g \cdot\left(z_{2}-z_1 \right) \cdot s^{2}}{S^{2}-s^{2}}}} \end{array}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Clepsydre antique
✔ RAI/ANA : Construire un raisonnement
Un cylindre de section S = 1 m2, rempli initialement
d'eau à une hauteur h_{0} = 1 m, se vide par un petit trou de section s = 1 cm2, au centre du fond.




1. Réaliser un schéma du système et exprimer le débit volumique à travers le trou en fonction de \frac{\mathrm{d} h(\mathrm{t})}{\mathrm{d} t}, en
utilisant la définition du débit volumique D_{v}=\frac{\mathrm{d} V}{\mathrm{d} t}.
2. Écrire la relation de Bernoulli. On supposera que l'écoulement est stationnaire. En déduire une relation entre \frac{\mathrm{d} h(t)}{\mathrm{d} t}, S, s, h(t) et g.
2. Écrire la relation de Bernoulli. On supposera que l'écoulement est stationnaire. En déduire une relation entre \frac{\mathrm{d} h(t)}{\mathrm{d} t}, S, s, h(t) et g.
3. Exprimer la durée nécessaire pour que le cylindre se vide complètement. On admet que h(t) est de la
forme h(t)=(a · t+b)^{2}, avec a et b deux constantes.
On souhaite réaliser une clepsydre de forme différente, pour laquelle la variation de hauteur d'eau est constante au cours du temps, c'est‑à‑dire telle que \frac{\mathrm{d} h}{\mathrm{d} t}=-\alpha, avec \alpha une constante positive.
4. Déterminer la relation entre la surface S et la hauteur h qui vérifie cette condition.
5. Exprimer la durée pour vider cette clepsydre.
On souhaite réaliser une clepsydre de forme différente, pour laquelle la variation de hauteur d'eau est constante au cours du temps, c'est‑à‑dire telle que \frac{\mathrm{d} h}{\mathrm{d} t}=-\alpha, avec \alpha une constante positive.
4. Déterminer la relation entre la surface S et la hauteur h qui vérifie cette condition.
5. Exprimer la durée pour vider cette clepsydre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29Jet d'eau de Genève
✔ REA : Utiliser un modèle
La ville de Genève est connue pour son jet d'eau sur le lac Léman. Initialement conçu pour évacuer les surpressions du réseau d'eau de la ville, il est devenu une attraction touristique.
1. Calculer la vitesse du jet d'eau au niveau du sol, en utilisant la relation de Bernoulli.
2. Calculer la puissance fournie par la pompe sur le fluide, initialement au repos dans le lac.
1. Calculer la vitesse du jet d'eau au niveau du sol, en utilisant la relation de Bernoulli.
2. Calculer la puissance fournie par la pompe sur le fluide, initialement au repos dans le lac.
Données
- Hauteur maximale du jet : h = 140 m
- Débit volumique : D_{\rm{V}} = 500 L·s-1
- Intensité de pesanteur : g = 9{,}81 N·kg-1


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30Balance hydrostatique
✔ APP : Extraire l'information utile
L'Encyclopédie de Diderot et d'Alembert (1751) explique comment utiliser une balance hydrostatique pour mesurer la densité d'un fluide.
Doc. 1
Schéma d'une balance hydrostatique

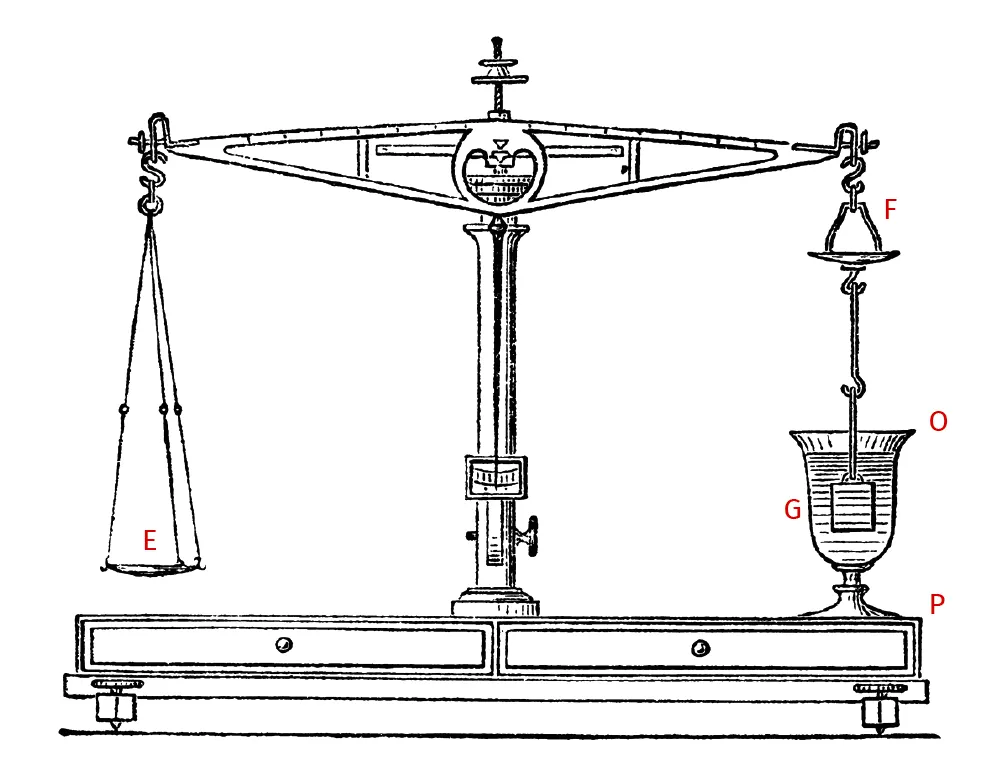
Expliquer la méthode proposée dans le doc. 2 en réalisant des schémas des étapes clés. Effectuer un bilan des forces pour justifier la mesure.
Cliquez pour accéder à une zone de dessin
Doc. 2
Extrait de l'Encyclopédie


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AJeté d'ancre
✔ APP : Faire des prévisions à l'aide d'un modèle
On considère un bateau de masse m_1 flottant sur un lac. Le bateau contient une ancre en acier de masse m_2 et de volume V_2.
1. Exprimer le volume d'eau déplacé V par le bateau.
Ensuite, le bateau jette l'ancre.
2. Exprimer V' le nouveau volume d'eau déplacé par le bateau et V" celui déplacé par l'ancre.
3. Le niveau de l'eau est‑il monté ou a‑t‑il baissé ?
On considère un bateau de masse m_1 flottant sur un lac. Le bateau contient une ancre en acier de masse m_2 et de volume V_2.
1. Exprimer le volume d'eau déplacé V par le bateau.
Ensuite, le bateau jette l'ancre.
2. Exprimer V' le nouveau volume d'eau déplacé par le bateau et V" celui déplacé par l'ancre.
3. Le niveau de l'eau est‑il monté ou a‑t‑il baissé ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BCanette percée
✔ REA : Appliquer une formule
Le fond d'une canette remplie d'eau cylindrique de section S et de hauteur h est percé d'un trou de section s. La pression de l'air dans la canette et à l'extérieur de la canette est supposée égale à la pression atmosphérique.
1. En utilisant la relation de Bernoulli entre deux points à préciser et la conservation du débit volumique, montrer que la vitesse à laquelle l'eau s'écoule vérifie : v = \sqrt{ \dfrac{ 2 \ g \cdot h} {1 - \dfrac{s^2}{S^2} }}
2. Calculer la vitesse de l'écoulement v.
3. Calculer la durée nécessaire pour vider entièrement la canette.
Le fond d'une canette remplie d'eau cylindrique de section S et de hauteur h est percé d'un trou de section s. La pression de l'air dans la canette et à l'extérieur de la canette est supposée égale à la pression atmosphérique.
1. En utilisant la relation de Bernoulli entre deux points à préciser et la conservation du débit volumique, montrer que la vitesse à laquelle l'eau s'écoule vérifie : v = \sqrt{ \dfrac{ 2 \ g \cdot h} {1 - \dfrac{s^2}{S^2} }}
2. Calculer la vitesse de l'écoulement v.
3. Calculer la durée nécessaire pour vider entièrement la canette.
Données
- Intensité de la pesanteur terrestre : g = 9{,}81 N·kg-1
- Masse volumique de l'eau : \rho_{eau} = 1{,}0 \times 10^3 kg·m-3
- Hauteur de la poche : h = 11{,}5 cm
- Section de la poche : S = 34 cm2
- Section du trou : s = 30 mm2
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
