Mathématiques Cycle 4
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 4
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62Développer une aire
✔ Je modélise une situation à l'aide d'une expression mathématique
✔ Je choisis un cadre adapté (numérique, algébrique ou géométrique) pour traiter un problème
Quand on multiplie la longueur et la largeur dʼun rectangle par 3, par combien multiplie-t-on son aire ?
✔ Je choisis un cadre adapté (numérique, algébrique ou géométrique) pour traiter un problème
Quand on multiplie la longueur et la largeur dʼun rectangle par 3, par combien multiplie-t-on son aire ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Quand on fait face à un problème, le plus simple est souvent de le représenter à l'aide d'un schéma afin de mieux nous représenter le phénomène pour pouvoir passer de l'écriture naturelle à l'écriture mathématique.
Corrigé 1
- Dessinez un rectangle quelconque.
- Multipliez sa longueur par 3. Cela revient à aligner 3 rectangles en longueur.
- Multipliez sa largeur par 3. Cela revient à aligner 3 rectangles en largeur.
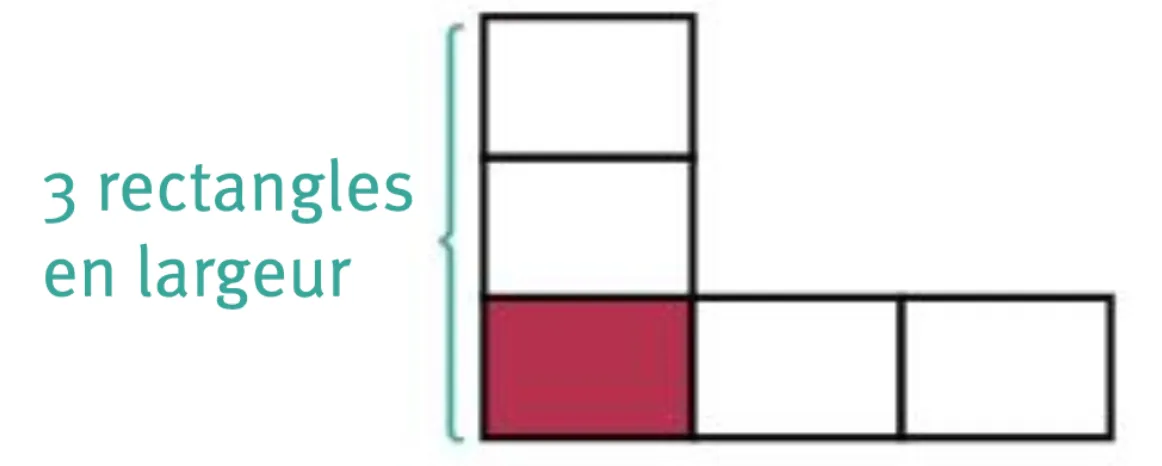
- Il ne reste plus qu'à compléter le dessin pour obtenir un rectangle complet.
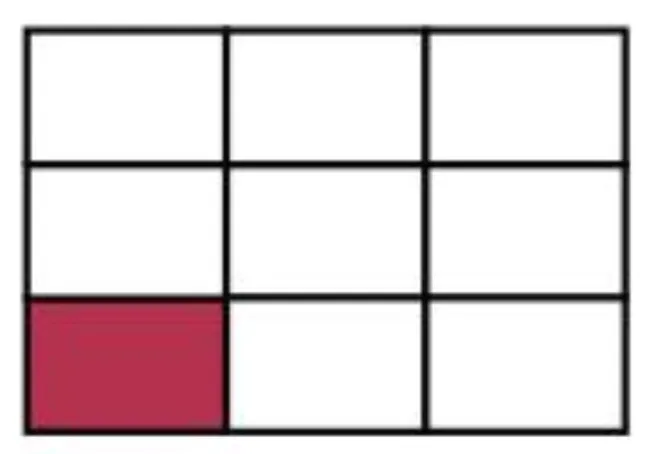
- Le nouveau rectangle est formé de 9 fois le rectangle initial.
L'aire a donc été multipliée par 9.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Quand on fait face à un problème, le plus rapide est de le transformer en une expression littérale qui permette de répondre à la question en utilisant le langage mathématique. Pour cela, il faut déterminer :
- les informations dont on dispose ;
- les informations qui ne sont pas à notre disposition mais dont on a besoin.
Corrigé 2
- Exprimez la situation de départ.
Posez \color{00a65f}l la largeur d'un rectangle quelconque, et \color{c21546} L sa longueur. Son aire A vaut : A = {\color{c21546}L} \times {\color{00a65f}l}. - Exprimez la situation d'arrivée.
Puisque l'on multiplie la largeur et la longueur par 3, la nouvelle aire A^{\prime} vaut maintenant : A^{\prime} = {\color{c21546}3} \times {\color{c21546}L} \times {\color{00a65f}3} \times {\color{00a65f}l}.
Dans une multiplication de plusieurs facteurs, on peut changer les facteurs de place. Donc :
A^{\prime} = {\color{c21546}3} \times {\color{00a65f}3} \times {\color{c21546}L} \times {\color{00a65f}l}
A^{\prime} = 9 \times {\color{c21546}L} \times {\color{00a65f}l}
A^{\prime} = 9 \times A - L'aire a donc été multipliée par 9.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème similaireVoir p. 94 : Spirale de Fibonnaci.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
