Retranscrire une situation réelle sous la forme d'une expression littérale s'appelle modéliser une situation. Il faut toujours définir les lettres introduites.

J'applique

Consigne :
ABCD est un rectangle.

a. Combien vaut le périmètre de ABCD ?
b. Faites le calcul si AB = 1 et AD = 10.
c. . Combien vaut l'aire du rectangle ?

Correction :
a. Le périmètre de ABCD vaut a + b + a + b = 2 \times a + 2 \times b.
b. AB = 1 et AD = 10, alors a = 1 et b = 10, donc le périmètre de ABCD vaut 2 \times 1 + 2 \times 10 = 22.
c. Son aire vaut a \times b.

Définition

Dans une expression littérale, les lettres que l'on utilise à la place des nombres sont appelées variables.

Exercices n° 1 à 25
p.84-87

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Simplification

Notations

Dans une expression littérale, il est possible de simplifier la notation, notamment en supprimant le signe « x » de la multiplication lorsqu'il est placé entre :

2 variables ;
un chiffre et une variable ;
un chiffre et une parenthèse ;
deux parenthèses.

On note aussi x^2 le produit de x \times x et x^3 le produit de x \times x \times x.

Exemples :

a \times b = ab

b \times 10 = 10 \times b = 10b

3 \times (a + 5) = 3 (a + 5)

(2 - a) \times (b + 5) = (2 - a)(b +5)

2 \times \pi \times r = 2\pi r

Remarque : On essaye toujours de noter 10b plutôt que b10.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Utilisation des expressions littérales

Définition

Deux expressions littérales sont égales si elles prennent toujours la même valeur quand on remplace les lettres par n'importe quel nombre.
Pour montrer que deux expressions littérales ne sont pas égales, il suffit de donner un contre-exemple.

Exercices n° 1 à 4
p.84-85

Attention

Pour a = 0, on a bien 5(3 + 0) = 0 + 15. Pourtant, ces expressions sont bien différentes.

J'applique

Consigne :
Les expressions suivantes sont-elles égales ?

(a + 5) + 3 et a + 8 ;
5 (3 + a) et a +15.

Correction :

Pour tout nombre a, d'après les règles sur les parenthèses :
(a + 5) + 3 = a + 5 + 3
(a + 5) + 3 = a + 8
Donc les expressions sont égales.

Pour tout a = 1, on a 5 (3 + a) = 5 (3 + 1) = 20 et a + 15 = 1 + 15 = 16.
a \neq 20
Donc ces expressions sont différentes.

Notation

Dans les formules, on utilise le signe « = » pour indiquer que plusieurs grandeurs sont les mêmes.

J'applique

Consigne :
Si un objet se déplace à une vitesse moyenne v sur une distance d en un temps t, alors v = \dfrac{d}{t}.
Un coureur de marathon parcourt 28 km en deux heures. À quelle vitesse court-il ?

Correction :
d = 28, t = 2 et v = \dfrac{d}{t} donc v = \dfrac {28}{2} = 14. Le coureur a donc une vitesse de 14 km/h.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Développement et factorisation

J'approfondis

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Distributivité

Propriété

Pour tout nombre {\color{#ab4657}k}, {\color{#648e82}m} et {\color{#648e82}n}.
On a toujours {\color{#ab4657}{\color{#ab4657}k}} \times ({\color{#648e82}m} + {\color{#648e82}n}) = {\color{#ab4657}k} \times {\color{#648e82}m} + {\color{#ab4657}k} \times {\color{#648e82}n}

Exercices n° 26 à 37
p.87-88

Cette propriété se transpose aussi en géométrie :

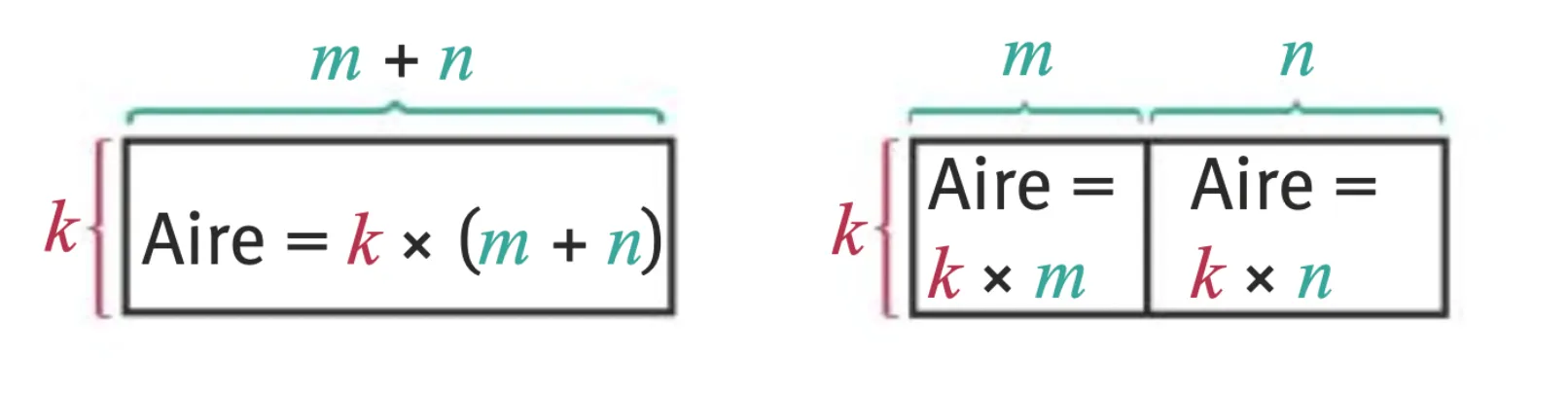
Schéma: factorisation d'aire de rectangle k(m+n) en deux parties k*m et k*n.

Remarque : La propriété de distributivité permet de transformer une somme en produit, ou un produit en somme.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Développement et factorisation

Définition

Développer une expression, c'est transformer un produit en somme grâce à la propriété de distributivité.

Exercices n° 26 à 37
p.87-88

Remarques :

Développer permet de calculer de tête :
8 \times 16 = 8 \times (10 + 6)
8 \times 16 = 8 \times 10 + 8 \times 6
8 \times 16 = 80 + 48
8 \times 16 = 128

Développer permet aussi de simplifier des expressions :
-(a + b) = (-1) \times (a + b)
-(a + b) = (-1) \times a + (-1) \times n
-(a + b) = -a + (-b)
-(a + b) = -a -b

J'applique

Consigne :
Développez l'expression 3 (5 + x).

Correction :

3 (5 + x) = 3 \times (5 + x)
3 (5 + x) = 3 \times 5 + 3 \times x
3 (5 + x) = 15 + 3x

Définition

Factoriser une expression, c'est transformer une somme en produit grâce à la propriété de distributivité.

Exercices n°

1 à 25

p.42-56

Aide

Pour factoriser, il faut trouver le facteur commun dans les différents termes de la somme.

Remarque : Développer ou factoriser permet de réduire une expression. On l'écrit avec le moins de nombres et de symboles possibles.

J'applique

Consigne :
Factorisez l'expression
8z + 5z.

Correction :

8z + 5z = z \times + z \times 5
8z + 5z = z \times (8 + 5)
8z + 5z = z \times 13
8z + 5z = 13z

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

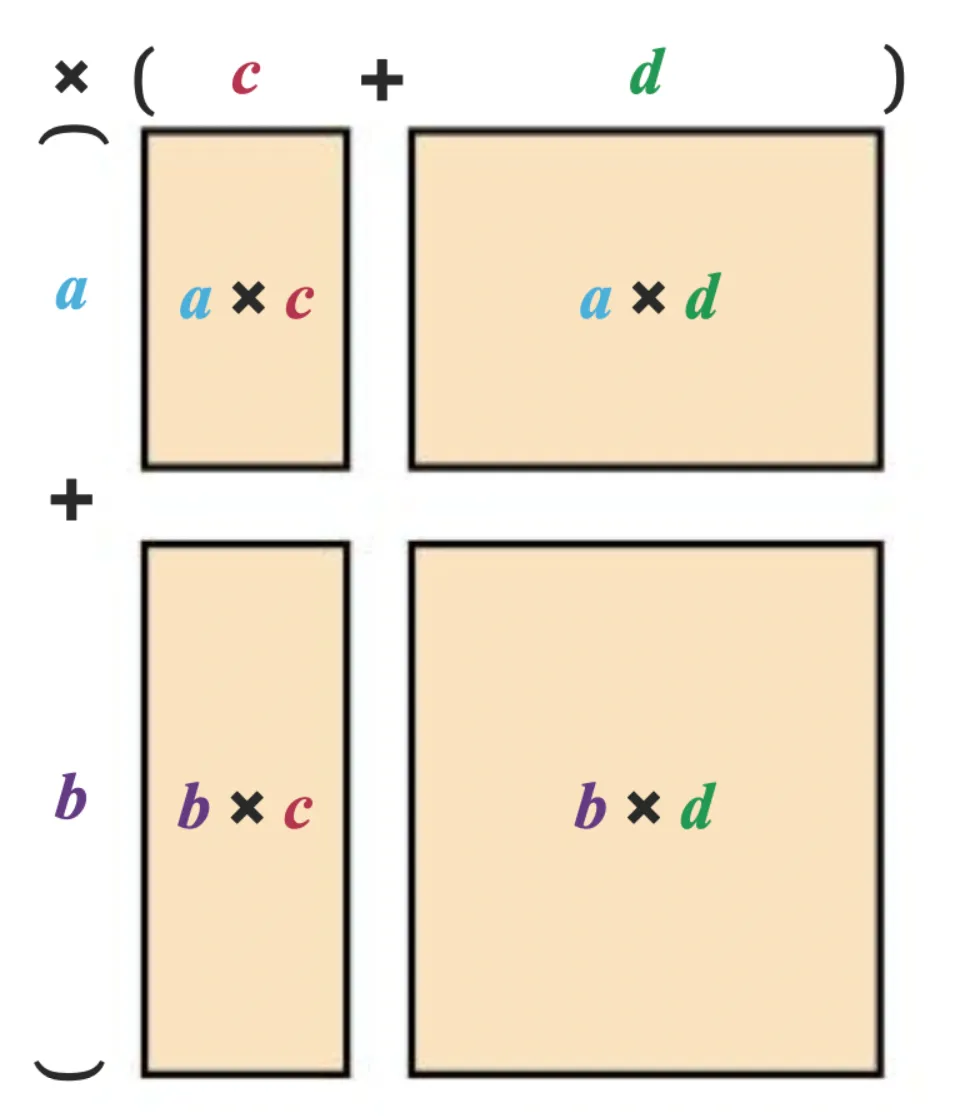
3
Je perfectionne
Développement double

Propriété

On a toujours :
({\color{#3ab4e0}a} + {\color{#6e2d88}b})({\color{#c21546}c} + {\color{#00a65f}d}) = {\color{#3ab4e0}a} \times {\color{#c21546}c} + {\color{#3ab4e0}a} \times {\color{#00a65f}d} + {\color{#6e2d88}b} \times {\color{#c21546}c} + {\color{#6e2d88}b} \times {\color{#00a65f}d}

Exercices n° 38 à 41
p.88-89

Schéma illustrant le développement de (a+b)(c+d) : quatre rectangles représentant les produits axc, axd, bxc et bxd.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Je perfectionne
Les identités remarquables

Propriété

Ces égalités sont toujours vraies, pour tous nombres {\color{#ab4657}a} et {\color{#3ab4e0}b} :

\begin{aligned} &({\color{#ab4657}a}+{\color{#3ab4e0}b})^{2}={\color{#ab4657}a}^{2}+2 {\color{#ab4657}a} {\color{#3ab4e0}b}+{\color{#3ab4e0}b}^{2} \\ &({\color{#ab4657}a}-{\color{#3ab4e0}b})^{2}={\color{#ab4657}a}^{2}-2 {\color{#ab4657}a} {\color{#3ab4e0}b}+{\color{#3ab4e0}b}^{2} \\ &({\color{#ab4657}a}+{\color{#3ab4e0}b})({\color{#ab4657}a}-{\color{#3ab4e0}b})={\color{#ab4657}a}^{2}-{\color{#3ab4e0}b}^{2} \end{aligned}

Exercices n° 58 à 61
p.91

Aide

On peut démontrer ces propriétés avec la géométrie.

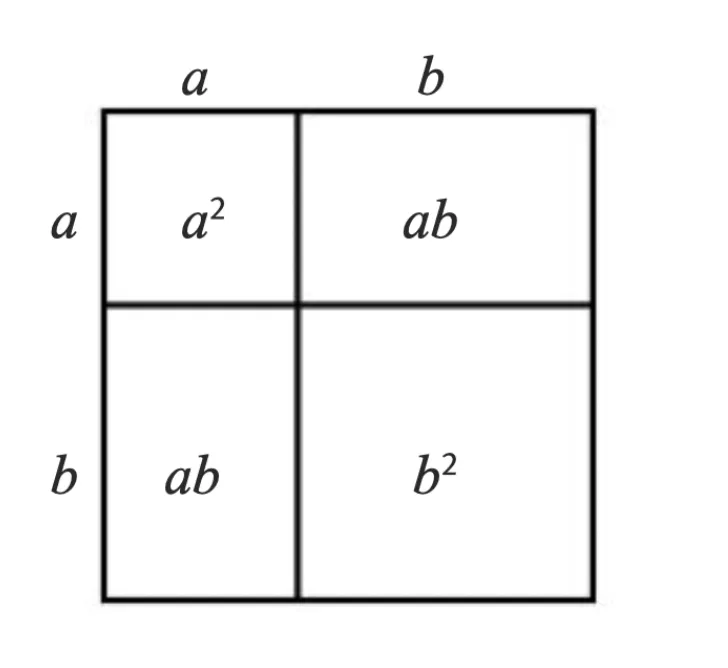
Schéma carré illustrant l'identité remarquable (a+b)² = a² + 2ab + b²

Aire = (a + b)^2
Aire = a^2 + ab + ab + b^2

Schéma illustrant l'identité remarquable (a-b)² : carré de côté a, divisé en quatre parties.

Aire = (a - b)^2
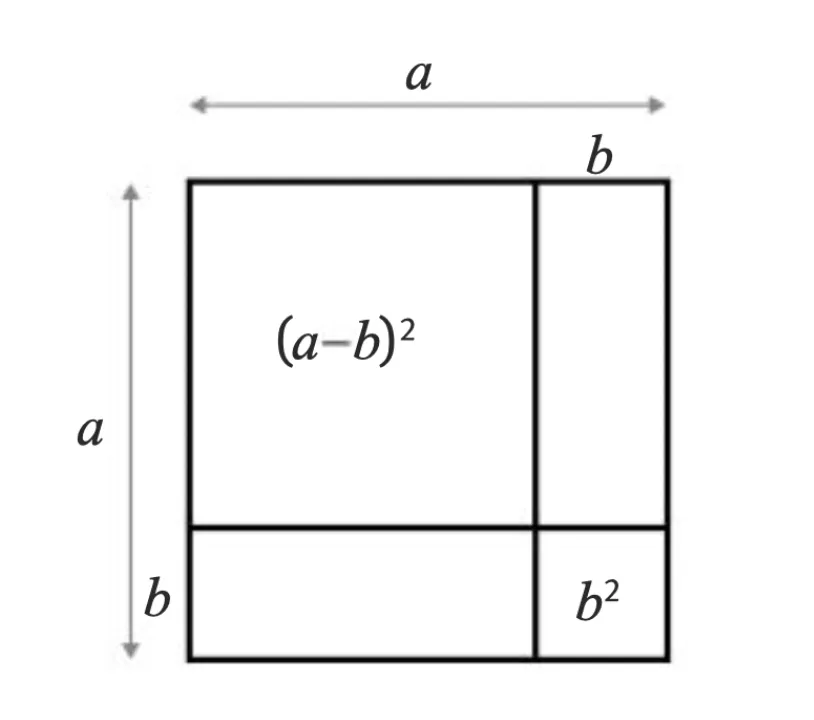
Aire = a^2 - ab - ab + b^2

J'applique

Consigne :
Factorisez l'expression 4a^2 + 20a + 25.

Correction :
4a^2 + 20a + 25 = (2a)^2 + 2 \times 2a \times 5 + 5 \times 5
4a^2 + 20a + 25 = (2a + 5)^2

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

C
Démontrer une propriété par le calcul littéral

Je perfectionne

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Utilisation

On peut montrer que deux expressions littérales sont égales à l'aide d'un calcul littéral.

Exercices n° 58 à 61
p.91

J'applique

Consigne :
Montrez que pour tous nombres a, b, c avec c \neq 0 :

\dfrac {a}{c} + \dfrac {b}{c} = \dfrac {a + b}{c}.

Aide

Le fait d'utiliser des lettres permet de montrer que les égalités sont vraies tout le temps et pas seulement dans des cas particuliers.

Correction :
À l'aide de la propriété de distributivité, nous obtenons :

\left(\dfrac{a}{c} + \dfrac{b}{c}\right) \times c = \dfrac{a}{c} \times c + \dfrac{b}{c} \times c = a + b

donc \left(\dfrac{a}{c} + \dfrac{b}{c}\right) \times \dfrac{c}{c} = \dfrac{a + b}{c}

On a donc bien \dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Mathématiques Cycle 4

Calcul littéral

AExpression littérale

1 Définitions

J'applique

2 Simplification

3 Utilisation des expressions littérales

J'applique

J'applique

BDéveloppement et factorisation

1 Distributivité

2 Développement et factorisation

J'applique

J'applique

3 Je perfectionneDéveloppement double

4 Je perfectionneLes identités remarquables

J'applique

CDémontrer une propriété par le calcul littéral

J'applique

Une erreur sur la page ? Une idée à proposer ?

A
Expression littérale

1
Définitions

2
Simplification

3
Utilisation des expressions littérales

B
Développement et factorisation

1
Distributivité

2
Développement et factorisation

3
Je perfectionne
Développement double

4
Je perfectionne
Les identités remarquables

C
Démontrer une propriété par le calcul littéral