Préparer le bac

Au 1^er janvier 2019, Sophie installe une éolienne dans son jardin. Une éolienne correctement orientée produit environ 200 kWh/an.
La première année, l'installation produit effectivement cette quantité d'énergie. Pour des raisons liées aux changements climatiques, on estime que la quantité d'énergie produite baissera de 4 % par an au cours des années suivantes.

Pour tout entier n \geqslant 0, on note u_n la quantité d'énergie produite par l'installation en kWh durant l'année 2019 + n.

1. a. Quelle est la valeur de u_{0} ? Calculer alors la quantité d'énergie produite par l'installation durant l'année 2020.

b. Pour tout entier naturel n, exprimer u_{n+1} en fonction de u_n.

c. Quelle est la nature de la suite \left(u_{n}\right) ? Préciser ses éléments caractéristiques.

d. Quelles sont les variations de la suite \left(u_{n}\right) ?

2. Pour calculer les termes successifs de la suite \left(u_{n}\right), Sophie utilise l'algorithme en Python ci-dessous.

def production(n):
  u = ...
  k = 0
  while k < n:
    ...
    k = k + 1
  return u 

a. compléter cet algorithme.
b. Quelle valeur est renvoyée par l'instruction production(5) ? On arrondira le résultat au centième près. Interpréter le résultat dans le contexte de l'exercice.

1. a. u_{0} correspond à l'énergie produite, en \text{kWh}, en 2019. Donc u_{0}=200. La quantité d'énergie baisse de 4 \% chaque année, ce qui revient à multiplier par 0{,}96. Donc la quantité d'énergie produite en 2020 est 0{,}96 \times 200=192 \mathrm{kWh}.
b. Pour calculer l'énergie produite l'année suivante, il faut diminuer de 4 \% l'énergie produite l'année précédente. Ainsi, pour tout entier naturel n, on a u_{n+1}=0{,}96 u_{n}.
c. On observe que la relation de récurrence est de la forme u_{n+1}=q \times u_{n} , avec q = 0{,}96. Ainsi, la suite \left(u_{n}\right) est géométrique.
La raison de cette suite est q = 0{,}96 et son premier terme est u_{0}=200.
d. La raison de cette suite géométrique est comprise entre 0 et 1, et u_{0}>0. La suite \left(u_{n}\right) est donc décroissante.

2. a.

def production(n):
  u = 200
  k = 0
  while k < n:
    u = 0.96*u
    k = k + 1
  return u

b. On exécute l'algorithme pour n = 5.
Ainsi, la boucle while tourne tant que k \lt 5 . L'algorithme renvoie alors la valeur u=163{,}07. On a donc effectué le calcul pour l'année 2019 + 5 = 2024. Cela signifie que l'énergie produite par l'éolienne en 2024 est estimée à 163{,}07 \text{ kWh}.

Le nuage de points ci-dessous représente les six premiers termes d'une suite u.

Une entreprise de maintenance d'ascenseurs estime que le nombre d'interventions effectuées chaque année augmente de 4 %. En 2019, ses 20 salariés ont effectué 1\,200 interventions.

1. Combien peut-on prévoir d'interventions en 2020 ? En 2021 ?

Pour tout entier naturel n, on note u_n le nombre annuel d'interventions effectuées par la société durant l'année 2019 + n.

2. a. Quelle est la valeur de u_0 ?

2. b. Pour tout entier naturel n, montrer que u_{n+1}=1{,}04 u_{n} et en déduire la nature de la suite \left(u_{n}\right) ainsi que son sens de variation.

3. L'entreprise décide d'embaucher un nouveau salarié à chaque palier de 200 interventions annuelles supplémentaires. Le programme ci-dessous est écrit en Python.

def ascenseurs(n):
  L = [1200]
  for i in range(n):
    L.append(int(L[i]*1.04))
  return L

Lorsque l'instruction ascenseurs(20) est exécutée, l'algorithme renvoie la liste :
[1200, 1248, 1297, 1348, 1401, 1457, 1515, 1575, 1638, 1703, 1771, 1841, 1914, 1990, 2069, 2151, 2237, 2326, 2419, 2515, 2615].
Combien de salariés l'entreprise comptera-t-elle en 2039 ?

On se propose d'étudier l'évolution du nombre de souris d'une animalerie sur une période de six semaines. Initialement, ce nombre s'élève à 240 souris.
On peut modéliser ce nombre de souris au bout de n semaines par la suite \left(u_{n}\right) définie, pour tout entier naturel n (avec 0 \leqslant n \leqslant 6), par u_{n}=240-40 n.

Un laboratoire dispose d'une culture de 10^{10} bactéries. Un antibiotique est alors introduit, divisant par 4 le nombre de bactéries toutes les heures. On note u_n le nombre de bactéries au bout de n heures.


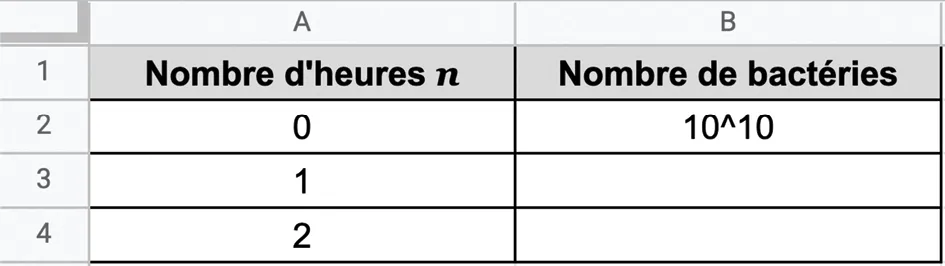
1. Quelle formule doit-on entrer dans la cellule B3 de sorte qu'en étirant cette formule vers le bas, on puisse compléter les lignes suivantes ?

2. Sans la déterminer, que représente concrètement la valeur qui se trouve dans la cellule B18 ?

3. Exprimer, pour tout entier naturel n, u_{n+1} en fonction de u_n.

4. Quelle est la nature de cette suite ? Quelle est sa raison ?

5. Compléter cet algorithme qui donne le nombre d'heures à partir duquel le nombre de bactéries deviendra inférieur à 100.