Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilit és
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 1
Cours 1
Suites numériques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A
Définitions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Une suite numérique u, ou (u_n), est une fonction dont l'ensemble de définition est \N = \{0 \; ; 1 \; ; 2 \; ; 3 \; ; 4 \; ; 5 \; ; \ldots\} ou une de ses parties.
À la variable entière n, on associe le nombre u(n) appelé terme de rang \bm n de la suite u.
On a donc u : n \mapsto u(n).
On note souvent u_n le terme de rang n.
À la variable entière n, on associe le nombre u(n) appelé terme de rang \bm n de la suite u.
On a donc u : n \mapsto u(n).
On note souvent u_n le terme de rang n.
Remarque
Lorsque la suite u est définie sur \N , le premier terme est le terme d'indice \bm 0, soit u_0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Soit (u_n) une suite définie sur \N dont les premiers termes sont : 2 \; ;-1 \; ;3{,}5 et \dfrac{1}{3}.
On a alors u(0)=2, u(1)=-1, u(2)=3{,}5 et u(3)=\dfrac{1}{3}.
On peut également écrire u_0=2, u_1=-1, u_2=3{,}5 et u_3=\dfrac{1}{3}.
On a alors u(0)=2, u(1)=-1, u(2)=3{,}5 et u(3)=\dfrac{1}{3}.
On peut également écrire u_0=2, u_1=-1, u_2=3{,}5 et u_3=\dfrac{1}{3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définitions
Dans le cadre des suites étudiées cette année, nous rencontrerons deux types de définition pour définir une suite (u_n) :
- par son terme général (ou écriture fonctionnelle) : il existe une fonction f telle que, pour tout n, u_n=f(n) ;
- par récurrence : dans ce cas, le terme suivant est défini par rapport au(x) terme(s) qui le précède(nt) et son (ou ses) premier(s) terme(s).
Remarques
- Pour une suite (u_n) définie par écriture fonctionnelle, u_n s'exprime directement en fonction de n. On peut donc directement calculer n'importe quel terme.
- Pour une suite (u_n) définie par récurrence, il est nécessaire de connaître un terme de la suite pour calculer les autres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
1. La suite (u_n) définie pour tout entier naturel n par u_n = 2n - 8 est une suite définie par son terme général.
2. La suite (v_n) définie par v_0 = 5 et la relation v_{n+1} = 2 v_n - 8, valable pour tout entier naturel n, est une suite définie par récurrence.
2. La suite (v_n) définie par v_0 = 5 et la relation v_{n+1} = 2 v_n - 8, valable pour tout entier naturel n, est une suite définie par récurrence.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 1
Calculer les termes d'une suite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Déterminer les trois premiers termes des suites (u_n) et (v_n) définies par les relations suivantes.
1. u_{n}=n^{2}+5 n-3.
2. v_{0}=2 et la relation, valable pour tout n \in \mathbb{N}, v_{n+1}=3 v_{n}+1.
1. u_{n}=n^{2}+5 n-3.
2. v_{0}=2 et la relation, valable pour tout n \in \mathbb{N}, v_{n+1}=3 v_{n}+1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. La suite (u_n) définie sur \N par u_{n}=n^{2}+5 n-3 est définie par écriture fonctionnelle avec f(n)=n^{2}+5 n-3.
On a donc u_{\color{darkred}0}={\color{darkred}0}^{2}+5 \times {\color{darkred}0}-3=-3 \; ; u_{\color{blue}1}={\color{blue}1}^{2}+5 \times {\color{blue}1}-3=3 et u_{\color{green}2}={\color{green}2}^{2}+5 \times {\color{green}2}-3=11.
2. La suite (v_n) est définie par récurrence.
On a déjà v_0=2, puis la relation de récurrence donne : {\color{darkred}v_{1}}=3 \times {\color{blue}v_{0}}+1=3 \times 2+1=7 puis {\color{darkred}v_{2}}=3 \times {\color{blue}v_{1}}+1=3 \times 7+1=22.
Pour s'entraîner : exercices
On a donc u_{\color{darkred}0}={\color{darkred}0}^{2}+5 \times {\color{darkred}0}-3=-3 \; ; u_{\color{blue}1}={\color{blue}1}^{2}+5 \times {\color{blue}1}-3=3 et u_{\color{green}2}={\color{green}2}^{2}+5 \times {\color{green}2}-3=11.
2. La suite (v_n) est définie par récurrence.
On a déjà v_0=2, puis la relation de récurrence donne : {\color{darkred}v_{1}}=3 \times {\color{blue}v_{0}}+1=3 \times 2+1=7 puis {\color{darkred}v_{2}}=3 \times {\color{blue}v_{1}}+1=3 \times 7+1=22.
Pour s'entraîner : exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On repère d'abord si la suite est définie par son terme général ou si elle est définie par récurrence.
1. La première suite est définie par son terme général : on a une expression de u_n en fonction de n. On remplace n par les valeurs voulues pour déterminer les termes demandés.
2. La seconde suite est définie par récurrence.
Ici, cette relation peut se traduire ainsi à l'oral : « terme suivant = 3 \times terme actuel + 1 ».
Attention, cette formulation n'a pas sa place sur une copie à l'écrit.
1. La première suite est définie par son terme général : on a une expression de u_n en fonction de n. On remplace n par les valeurs voulues pour déterminer les termes demandés.
2. La seconde suite est définie par récurrence.
Ici, cette relation peut se traduire ainsi à l'oral : « terme suivant = 3 \times terme actuel + 1 ».
Attention, cette formulation n'a pas sa place sur une copie à l'écrit.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B
Sens de variation d'une suite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définitions
Soit (u_n) une suite numérique.
- La suite (u_n) est croissante lorsque, pour tout entier naturel n, u_{n+1} \geqslant u_{n}, c'est-à-dire lorsque ses termes sont de plus en plus grands.
- La suite (u_n) est décroissante lorsque, pour tout entier naturel n, u_{n+1} \leqslant u_{n}, c'est-à-dire lorsque ses termes sont de moins en moins grands.
Remarque
Lorsque les inégalités sont strictes, on parle alors de stricte (dé)croissance.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
1. Soit (u_n) une suite vérifiant, pour tout entier naturel n, la relation de récurrence u_{n+1}=u_{n}-4.
Comme u_{n+1}=u_{n}-4, on en déduit que u_{n+1}\lt u_{n} et donc que la suite (u_n) est strictement décroissante.
2. Soit (v_n) une suite vérifiant, pour tout entier naturel n, v_{n+1}=v_{n}+n^{2}.
On sait qu'un carré est toujours positif ou nul. Ainsi, puisque v_{n+1}=v_{n}+n^{2}, on déduit que v_{n+1} \geqslant v_{n} et donc que la suite (v_n) est croissante.
Comme u_{n+1}=u_{n}-4, on en déduit que u_{n+1}\lt u_{n} et donc que la suite (u_n) est strictement décroissante.
2. Soit (v_n) une suite vérifiant, pour tout entier naturel n, v_{n+1}=v_{n}+n^{2}.
On sait qu'un carré est toujours positif ou nul. Ainsi, puisque v_{n+1}=v_{n}+n^{2}, on déduit que v_{n+1} \geqslant v_{n} et donc que la suite (v_n) est croissante.
Remarque
Il existe des suites qui ne sont ni croissantes, ni décroissantes.
Par exemple, les termes de la suite (u_n) définie, pour tout entier naturel n, par u_{n}=(-1)^{n} valent successivement 1, puis -1, puis 1, puis -1, etc.
Par exemple, les termes de la suite (u_n) définie, pour tout entier naturel n, par u_{n}=(-1)^{n} valent successivement 1, puis -1, puis 1, puis -1, etc.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 2
Déterminer le sens de variation d'une suite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Étudier le sens de variation de la suite (v_n) définie, pour tout entier naturel n, par v_{n}=-2 n+3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
On calcule, pour tout entier naturel n, la différence v_{n+1}-v_{n}.
Ici, \begin{aligned} v_{n+1}-v_{n} & =[-2(n+1)+3]-[-2 n+3] \\ & =-2 n-2+3+2 n-3=-2 \end{aligned}.
Ainsi, v_{n+1}-v_{n}\lt 0 et donc v_{n+1}\lt v_{n}.
La suite (v_n) est donc strictement décroissante.
Pour s'entraîner : exercices
Ici, \begin{aligned} v_{n+1}-v_{n} & =[-2(n+1)+3]-[-2 n+3] \\ & =-2 n-2+3+2 n-3=-2 \end{aligned}.
Ainsi, v_{n+1}-v_{n}\lt 0 et donc v_{n+1}\lt v_{n}.
La suite (v_n) est donc strictement décroissante.
Pour s'entraîner : exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour déterminer le sens de variation de la suite (v_n) :
- on calcule, pour tout n, la différence v_{n+1}-v_{n} ;
- on étudie le signe de la différence ;
- si la différence est positive, alors la suite (v_n) est croissante, si la différence est négative, alors la suite (v_n) est décroissante.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C
Représentation graphique d'une suite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Afin de mieux visualiser les variations d'une suite numérique (u_n), mais également la notion de limite qui sera au programme de la classe de Terminale, on peut représenter les termes de cette suite sur un graphique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Soit (u_n) une suite.
Dans un repère, la représentation graphique de la suite (u_n) est l'ensemble des points de coordonnées (n \; ; u_n).
Dans un repère, la représentation graphique de la suite (u_n) est l'ensemble des points de coordonnées (n \; ; u_n).
Le zoom est accessible dans la version Premium.
Remarque
Ce que l'on observe graphiquement sur les premiers termes n'est pas à généraliser pour l'ensemble de la suite mais permet d'émettre une conjecture.
Remarque
La représentation graphique obtenue est un nuage de points. Ce n'est pas une courbe.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 3
Représenter une suite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Représenter sur un graphique les quatre premiers termes des suites (v_n) et (w_n) définies par les relations suivantes.
1. v_{n}=n^{2}-\dfrac{1}{2} n+1.
2. w_{n+1}=\left(w_{n}-2\right)^{2}-1 et w_{0}=1.
1. v_{n}=n^{2}-\dfrac{1}{2} n+1.
2. w_{n+1}=\left(w_{n}-2\right)^{2}-1 et w_{0}=1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
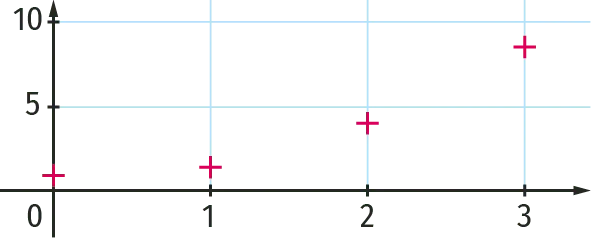
1. On calcule les quatre premiers termes de la
suite \left(v_{n}\right): v_{0}=1 \; ; v_{1}=\dfrac{3}{2} \; ; v_{2}=4 et v_{3}=\dfrac{17}{2}.
On place alors quatre points de coordonnées (0 \; ; 1) \; ;\left(1 \; ; \dfrac{3}{2}\right) \; ;(2 \; ; 4) et \left(3 \; ; \dfrac{17}{2}\right)
On place alors quatre points de coordonnées (0 \; ; 1) \; ;\left(1 \; ; \dfrac{3}{2}\right) \; ;(2 \; ; 4) et \left(3 \; ; \dfrac{17}{2}\right)
Le zoom est accessible dans la version Premium.
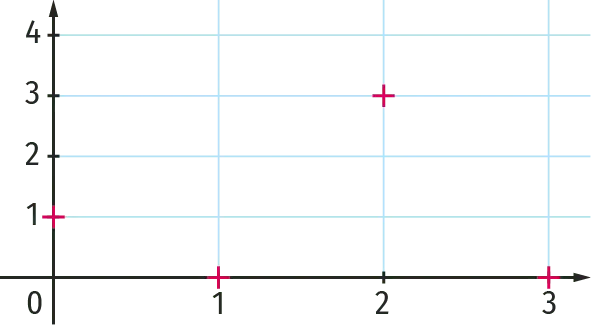
2. De même, on calcule les quatre premiers
termes de la suite \left(w_{n}\right): w_{0}=1 \; ; w_{1}=0 \; ; w_{2}=3 et w_3=0.
On place alors quatre points de coordonnées (0 \; ; 1) \; ;(1 \; ; 0) \; ;(2 \; ; 3) et (3 \; ; 0).
On place alors quatre points de coordonnées (0 \; ; 1) \; ;(1 \; ; 0) \; ;(2 \; ; 3) et (3 \; ; 0).
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- On détermine les quatre premiers termes de chacune des suites.
- On place les couples (n \; ; v_n) et (n \; ; w_n) dans un repère.
- Les nuages de points obtenus sont les représentations graphiques des deux suites. On ne relie surtout pas les points !
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah