Mathématiques 1re Techno
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 1
Entraînement 1
Suites numériques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 54[Calculer.]
Calculer, dans chaque cas, les termes de rang 0, 1, 2, 5 et 10 des suites indiquées.
1. u_{n}=2 n^{2}+3 n+1
2. v_{n}=-2 n+\dfrac{1}{n+1}
3. w_{n}=\dfrac{2 n+1}{n^{2}+1}
4. t_{n}=2^{n}
1. u_{n}=2 n^{2}+3 n+1
2. v_{n}=-2 n+\dfrac{1}{n+1}
3. w_{n}=\dfrac{2 n+1}{n^{2}+1}
4. t_{n}=2^{n}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 55[Calculer.]
Pour chacune des suites, exprimer u_{n+1} en fonction de n.
1. u_{n}=2 n+1
2. u_{n}=3 n^{2}-5 n+1
3. u_{n}=\dfrac{2 n}{n+1}
4. u_{n}=\sqrt{2 n}+n
1. u_{n}=2 n+1
2. u_{n}=3 n^{2}-5 n+1
3. u_{n}=\dfrac{2 n}{n+1}
4. u_{n}=\sqrt{2 n}+n
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 56[Calculer.]
Dans chacun des cas, déterminer les quatre premiers termes de la suite.
1. u_{n+1}=2 u_{n}-3 \text { et } u_{0}=1.
2. v_{n+1}=v_{n}^{2}-2 n \text { et } v_{0}=-1.
3. w_{n+1}=\dfrac{w_{n}+1}{n+1} \text { et } w_{0}=2.
4. t_{n+1}=\sqrt{t_{n}} \text { et } t_{0}=256.
1. u_{n+1}=2 u_{n}-3 \text { et } u_{0}=1.
2. v_{n+1}=v_{n}^{2}-2 n \text { et } v_{0}=-1.
3. w_{n+1}=\dfrac{w_{n}+1}{n+1} \text { et } w_{0}=2.
4. t_{n+1}=\sqrt{t_{n}} \text { et } t_{0}=256.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 57[Chercher.]
Dans chacun des cas, afficher sur la calculatrice la liste des premiers termes de la suite, puis conjecturer son sens de variation.
1. u_{n+1}=2 u_{n}+3 \text { et } u_{0}=1.
2. v_{n+1}=-v_{n}^{2} \text { et } v_{0}=2.
3. w_{n+1}=n w_{n}-n \text { et } w_{0}=3.
1. u_{n+1}=2 u_{n}+3 \text { et } u_{0}=1.
2. v_{n+1}=-v_{n}^{2} \text { et } v_{0}=2.
3. w_{n+1}=n w_{n}-n \text { et } w_{0}=3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 58Tableur[Modéliser.]
On souhaite calculer les termes d'une suite définie par récurrence à l'aide de la feuille de calcul suivante.

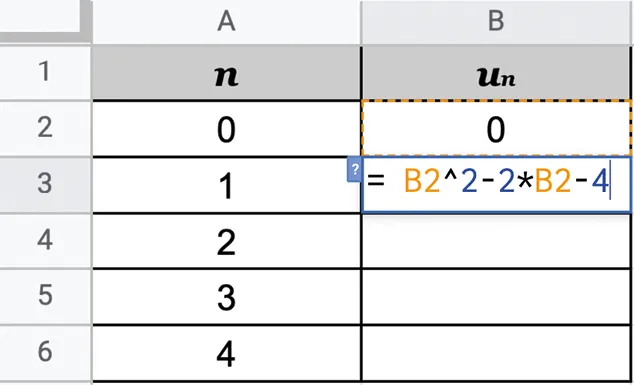
1. Quelle valeur apparaît dans la cellule B3 ?
2. Quelle relation de récurrence y a-t-il entre u_{n+1} et u_n ?


1. Quelle valeur apparaît dans la cellule B3 ?
2. Quelle relation de récurrence y a-t-il entre u_{n+1} et u_n ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 59Algo[Raisonner.]
On considère l'algorithme suivant, permettant de calculer les termes successifs de la suite (u_n) définie sur \N^*.
Déterminer, en justifiant, si les propositions suivantes sont vraies ou fausses.
1. La dernière valeur calculée par l'algorithme est \dfrac{11}{5}.
2. u_1=1.
3. Pour tout entier naturel non nul n, u_n=\dfrac{2n+1}{n}.
\boxed{
\begin{array} { r|l }
1 & \text{Pour } n \text{ allant de } 1 \text{ à } 5\\
2 & \quad \text{U}\leftarrow \dfrac{2n+1}{n}\\
3 & \text{Fin Pour}\\
\end{array}
}
Déterminer, en justifiant, si les propositions suivantes sont vraies ou fausses.
1. La dernière valeur calculée par l'algorithme est \dfrac{11}{5}.
2. u_1=1.
3. Pour tout entier naturel non nul n, u_n=\dfrac{2n+1}{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 60 [ Représenter.]
On définit les suites \left(u_{n}\right), \left(v_{n}\right) et \left(w_{n}\right) par u_{0}=v_{0}=w_{0}=3 et les relations de récurrence, valables pour tout entier naturel n, u_{n+1}=u_{n}-1, v_{n+1}=\dfrac{2}{3} v_{n} et w_{n+1}=3 w_{n}-7.
On a représenté les trois premiers termes de chacune des suites. Associer à chacune des suites le nuage de points correspondant.

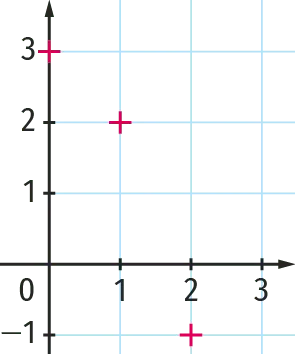

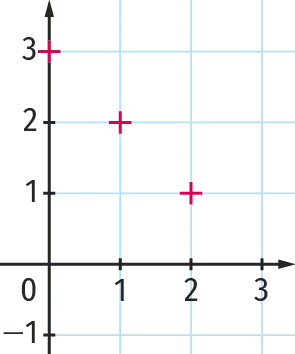

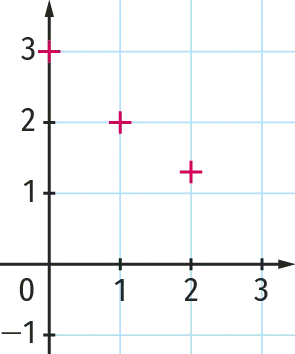
On a représenté les trois premiers termes de chacune des suites. Associer à chacune des suites le nuage de points correspondant.






Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 61 [ Calculer.]
Déterminer, dans chaque cas, le sens de variation de la suite.
1. u_{n}=n^{2}-2 n+1
2. v_{n}=-n
3. w_{n}=\frac{1}{n} \text { pour } n>0
4. t_{n}=\dfrac{n+5}{2 n+1}
1. u_{n}=n^{2}-2 n+1
2. v_{n}=-n
3. w_{n}=\frac{1}{n} \text { pour } n>0
4. t_{n}=\dfrac{n+5}{2 n+1}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 62 [ Modéliser.]
Après inscription à une salle de sport, la masse d'un homme de 90 kilos évolue chaque mois de la manière suivante :
Pour tout entier naturel n, on note v_n la masse de l'homme, en kilo, au bout de n mois.
1. Déterminer la valeur de v_0.
2. Exprimer v_{n+1} en fonction de v_n.
3. Quelle sera la masse de cet homme au bout de 3 mois ?
- il perd 4 % de sa masse ;
- il prend 1 kilo supplémentaire.
Pour tout entier naturel n, on note v_n la masse de l'homme, en kilo, au bout de n mois.
1. Déterminer la valeur de v_0.
2. Exprimer v_{n+1} en fonction de v_n.
3. Quelle sera la masse de cet homme au bout de 3 mois ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 63[ Modéliser.]
Un cybercafé propose le tarif suivant pour jouer en ligne : le client paie 3 € l'entrée au cybercafé auxquels s'ajoutent 2 € par heure de jeu.
Pour tout entier naturel n, on note n le nombre d'heures passées à jouer et u_n le prix à payer pour jouer n heures.
1. Exprimer u_n en fonction de n.
2. Combien le client va-t-il payer s'il joue 6 heures de suite ?
3. Résoudre dans \N l'inéquation u_n \geqslant 50, puis interpréter le résultat obtenu.
Pour tout entier naturel n, on note n le nombre d'heures passées à jouer et u_n le prix à payer pour jouer n heures.
1. Exprimer u_n en fonction de n.
2. Combien le client va-t-il payer s'il joue 6 heures de suite ?
3. Résoudre dans \N l'inéquation u_n \geqslant 50, puis interpréter le résultat obtenu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 64
[Calculer.]
On définit, pour tout entier naturel n, la suite (u_n) par : \left\{\begin{array}{c}
u_{n+2}=u_{n+1}-2 u_{n} \\
u_{0}=2 \text { et } u_{1}=4
\end{array}\right..
Calculer les cinq premiers termes de la suite.
Calculer les cinq premiers termes de la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 65[Calculer.]
Soient (u_n) et (v_n) deux suites définies pour tout entier naturel n par : \left\{\begin{array}{l}
u_{n+1}=2 u_{n}-v_{n} \\
v_{n+1}=v_{n}-2 u_{n} \\
u_{0}=4 \; ; v_{0}=-1
\end{array}\right..
Calculer les cinq premiers termes de ces deux suites.
Calculer les cinq premiers termes de ces deux suites.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 66[Modéliser.]
On étudie une population de brochets dans un étang, estimée à 1\, 500 individus en 2018. Chaque année, du fait de la pêche, la population de brochets diminue de 10 %. Pour compenser cette diminution, on décide d'aleviner et d'introduire 200 nouveaux poissons chaque année. Pour tout entier naturel n, on désigne par u_n le nombre de brochets vivant dans l'étang lors de l'année 2018 + n.
1. Que vaut u_0 ?
2. Justifier que pour tout entier naturel n : u_{n+1}=0{,}9 u_{n}+200.
3. À l'aide de la calculatrice, déterminer l'année à partir de laquelle la population de brochets dépassera 1\,950 individus.


1. Que vaut u_0 ?
2. Justifier que pour tout entier naturel n : u_{n+1}=0{,}9 u_{n}+200.
3. À l'aide de la calculatrice, déterminer l'année à partir de laquelle la population de brochets dépassera 1\,950 individus.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 67GeoGebra[ Représenter.]
Soit f la fonction définie, pour tout réel x, par f(x) = 1{,}5x - 4. Sur GeoGebra, on trace la courbe représentative de la fonction f et la droite d'équation y = x.
Soit (u_n) la suite définie par u_0=1 et la relation de récurrence, valable pour tout entier naturel n, u_{n+1}=f\left(u_{n}\right).
1. Placer u_0 sur l'axe des abscisses.
2. À l'aide de la courbe représentative de f, placer u_1 sur l'axe des ordonnées.
3. À l'aide de la droite d'équation y = x, placer u_1 sur l'axe des abscisses.
4. En procédant de la même manière, placer les termes u_2, u_3 et u_4.
Soit (u_n) la suite définie par u_0=1 et la relation de récurrence, valable pour tout entier naturel n, u_{n+1}=f\left(u_{n}\right).
1. Placer u_0 sur l'axe des abscisses.
2. À l'aide de la courbe représentative de f, placer u_1 sur l'axe des ordonnées.
3. À l'aide de la droite d'équation y = x, placer u_1 sur l'axe des abscisses.
4. En procédant de la même manière, placer les termes u_2, u_3 et u_4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 68[Calculer.]
On considère la suite (u_n) définie, pour tout entier naturel non nul n, par u_{n}=n+\dfrac{1}{n}.
1. Calculer les cinq premiers termes de la suite.
2. Pour tout entier naturel n non nul, exprimer u_{n+1} en fonction de n.
3. Montrer que la suite (u_n) est croissante.
1. Calculer les cinq premiers termes de la suite.
2. Pour tout entier naturel n non nul, exprimer u_{n+1} en fonction de n.
3. Montrer que la suite (u_n) est croissante.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 69[Chercher.]
On définit, pour tout entier naturel non nul n, la suite (u_n) comme la somme des n premiers entiers naturels non nuls 1 + 2 + 3 + 4 + 5 + \ldots+ n et la suite (v_n) par la relation v_{n}=\dfrac{n(n+1)}{2}.
1. Montrer que ces deux suites sont croissantes.
2. Calculer les cinq premiers termes de ces deux suites.
Quelle conjecture peut-on faire sur ces deux suites ?
On admettra dans la suite que cette conjecture est vraie.
3. En déduire la somme des 100 premiers entiers naturels.
1. Montrer que ces deux suites sont croissantes.
2. Calculer les cinq premiers termes de ces deux suites.
Quelle conjecture peut-on faire sur ces deux suites ?
On admettra dans la suite que cette conjecture est vraie.
3. En déduire la somme des 100 premiers entiers naturels.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 70 Exercice inversé
1.
Trouver une suite croissante et une suite décroissante définies par leur terme général.
2. Trouver une suite croissante et une suite décroissante définies par récurrence.
2. Trouver une suite croissante et une suite décroissante définies par récurrence.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 71 Exercice inversé
Les premiers termes d'une suite (v_n) sont : 1 \; ;
2 \; ; 4 \; ; 8 \; ; 16 \; ; 32 \; ; 64 et 128. Proposer une expression possible du terme général de v_n et une relation de récurrence vérifiée par (v_n).
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
