Physique-Chimie 3e - Cahier d'activités - 2023
Nouveau manuel de Sciences et Technologie 6e
Découvrez cet ouvrage collaboratif, conforme au nouveau programme !
Mes Pages
Thème 1 : Organisation et transformations de la matière
Ch. 1
Les espèces chimiques et l'identification
Ch. 2
Les transformations chimiques
Ch. 3
Les états de la matière
Ch. 4
Les mélanges et la solubilité
Ch. 5
L'organisation de la matière dans l'Univers
Thème : 2 Mouvements et interactions
Ch. 6
La vitesse des systèmes
Ch. 7
Les nature des mouvements
Ch. 8
La modélisation des actions
Thème 3 : Énergie, transferts et conversions
Ch. 9
Les différentes formes d’énergie et les conversions
Ch. 10
Les circuits électriques et les lois
Ch. 11
La puissance électrique et la consommation
Thème 4 : Signaux pour observer et communiquer
Ch. 12
Les signaux lumineux et sonores
Annexes
Fiches méthodes
Fiche méthode 7
Utiliser une formule
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthodologie
Une formule ou une équation représente une relation mathématique entre plusieurs grandeurs. Il n'est pas nécessaire de connaître toutes les équations basées sur une même relation, mais il faut être capable de passer d'une équation à une autre pour pouvoir isoler une grandeur.
La vitesse
La vitesse v d'un objet est liée à la distance d parcourue par cet objet pendant la durée t par la formule :
\begin{array}{l|l}
& d: \text { distance }(\mathrm{m}) \\
d=v \times t & v: \text { vitesse }(\mathrm{m} / \mathrm{s}) \\
& t: \text { durée }(\mathrm{s})
\end{array}
Cette équation permet de calculer la distance d en connaissant la vitesse v et la durée de parcours t. Elle sert aussi de base pour calculer t et v.
Pour calculer \bold{t} en connaissant \bold{d} et \bold{v} :

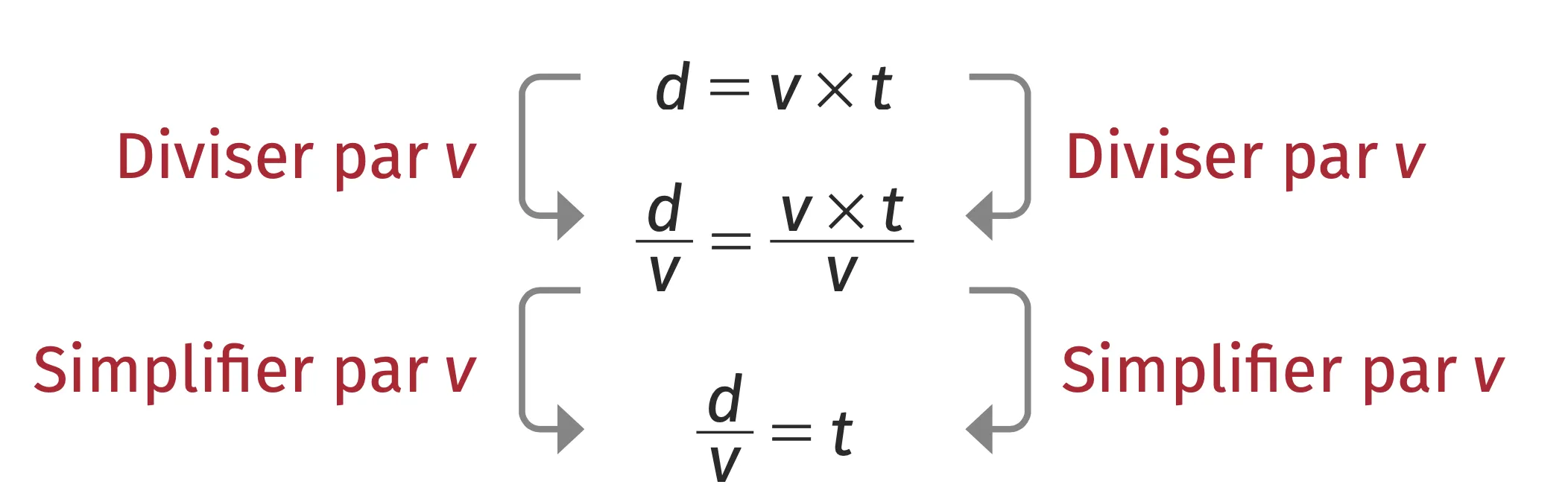
Il suffit ensuite de renverser le sens de l'égalité pour avoir l'expression de la durée t.

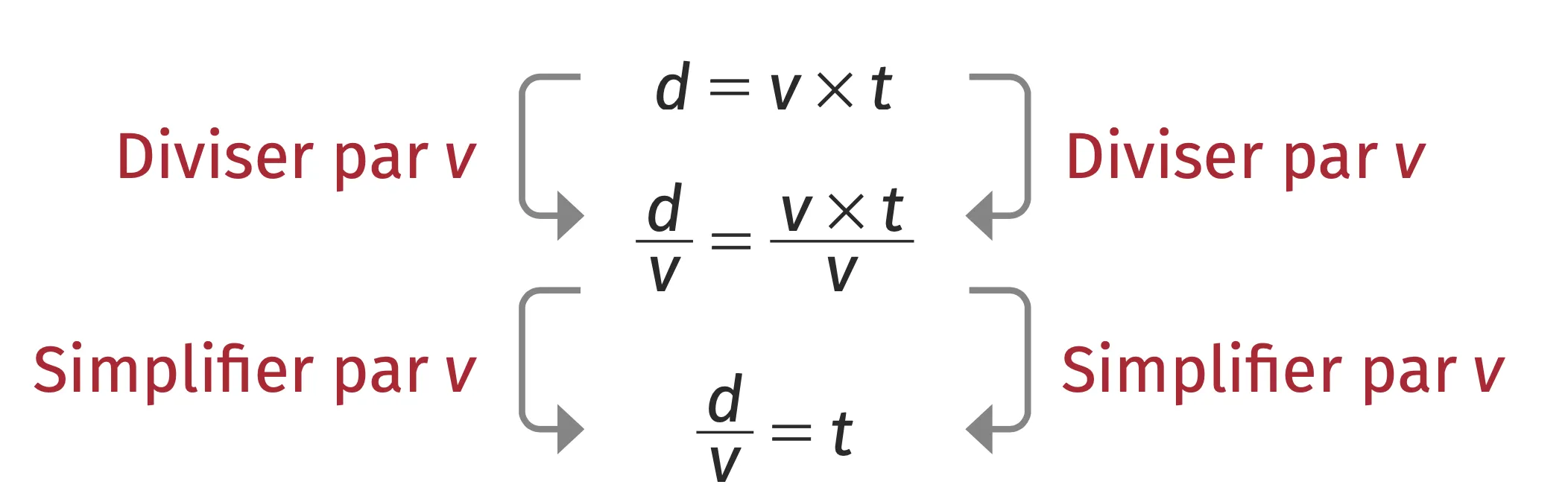
Il suffit ensuite de renverser le sens de l'égalité pour avoir l'expression de la durée t.
Pour calculer \bold{v} en connaissant \bold{d} et \bold{t} :

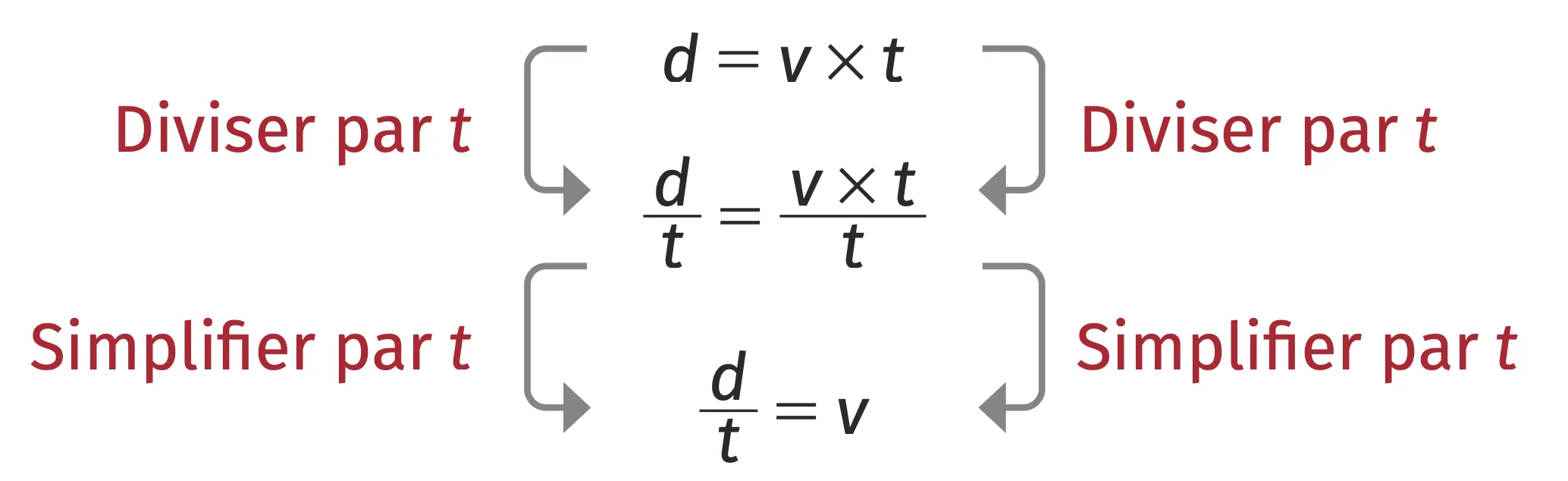
De la même façon, il suffit de renverser le sens de l'égalité pour obtenir l'expression de la vitesse v.

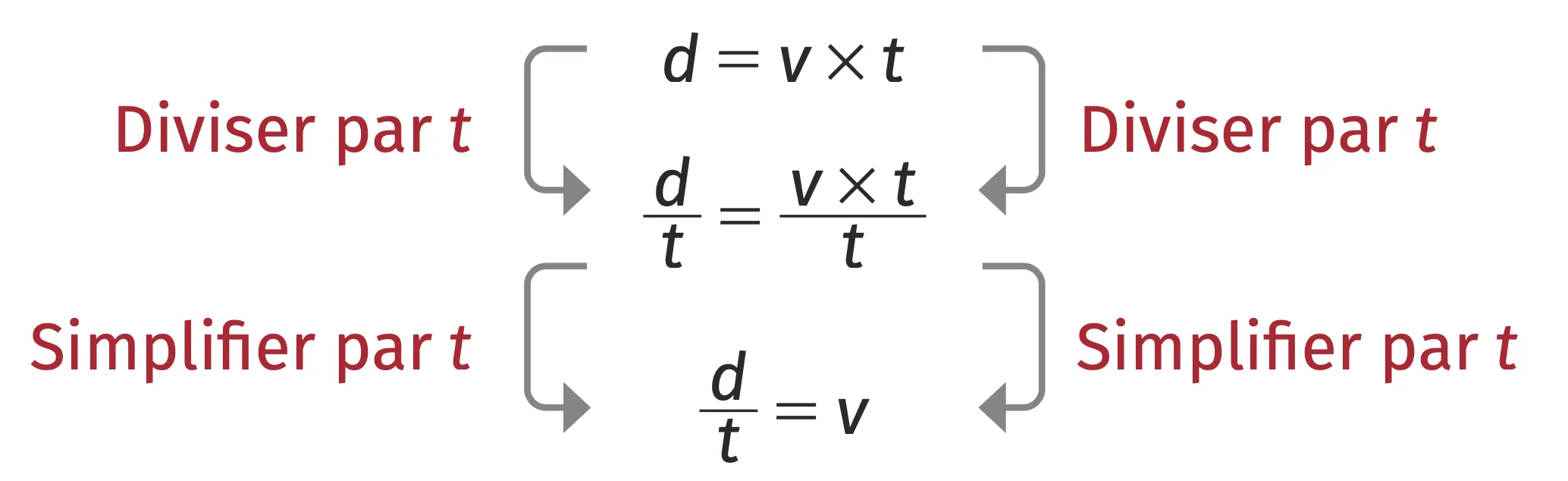
De la même façon, il suffit de renverser le sens de l'égalité pour obtenir l'expression de la vitesse v.
L'énergie cinétique
L'énergie cinétique E_{\mathrm{c}} d'un objet est reliée à la masse m de l'objet et à sa vitesse v par la formule :
\begin{array}{l|l}
E_{\mathrm{c}}=\frac{1}{2} \times m \times v^2 & E_{\mathrm{c}}: \text { énergie cinétique }(\mathrm{J}) \\
& m: \text { masse }(\mathrm{kg}) \\
& v: \text { vitesse }(\mathrm{m} / \mathrm{s})
\end{array}
Pour calculer \bold{m} en connaissant \bold{E_{\mathrm{c}}} et \bold{v} :

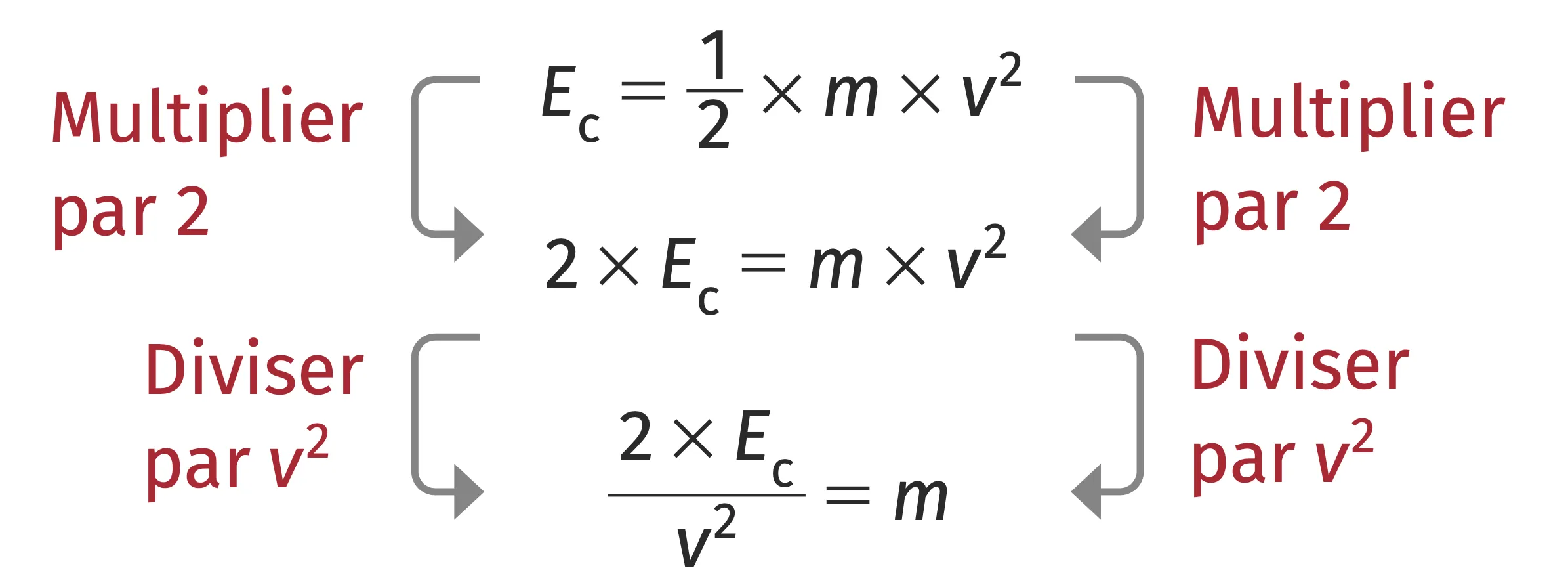

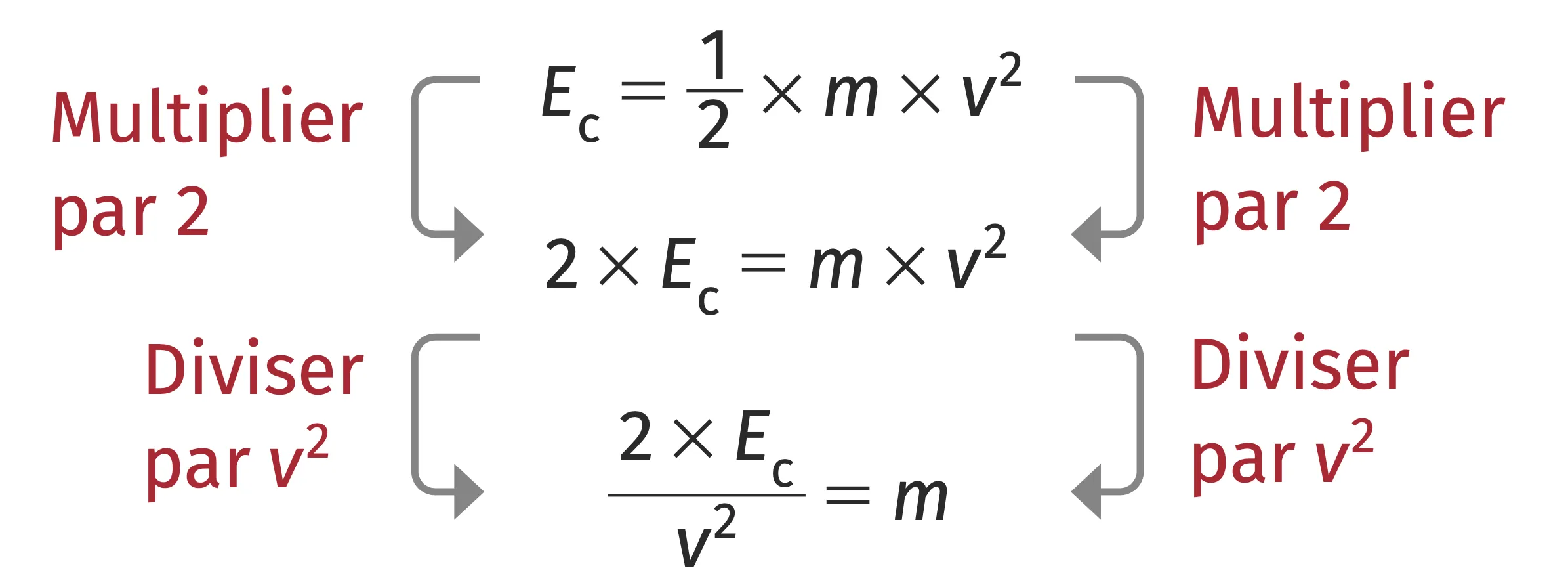
Pour calculer \bold{v} en connaissant \bold{E_{\mathrm{c}}} et \bold{m} :

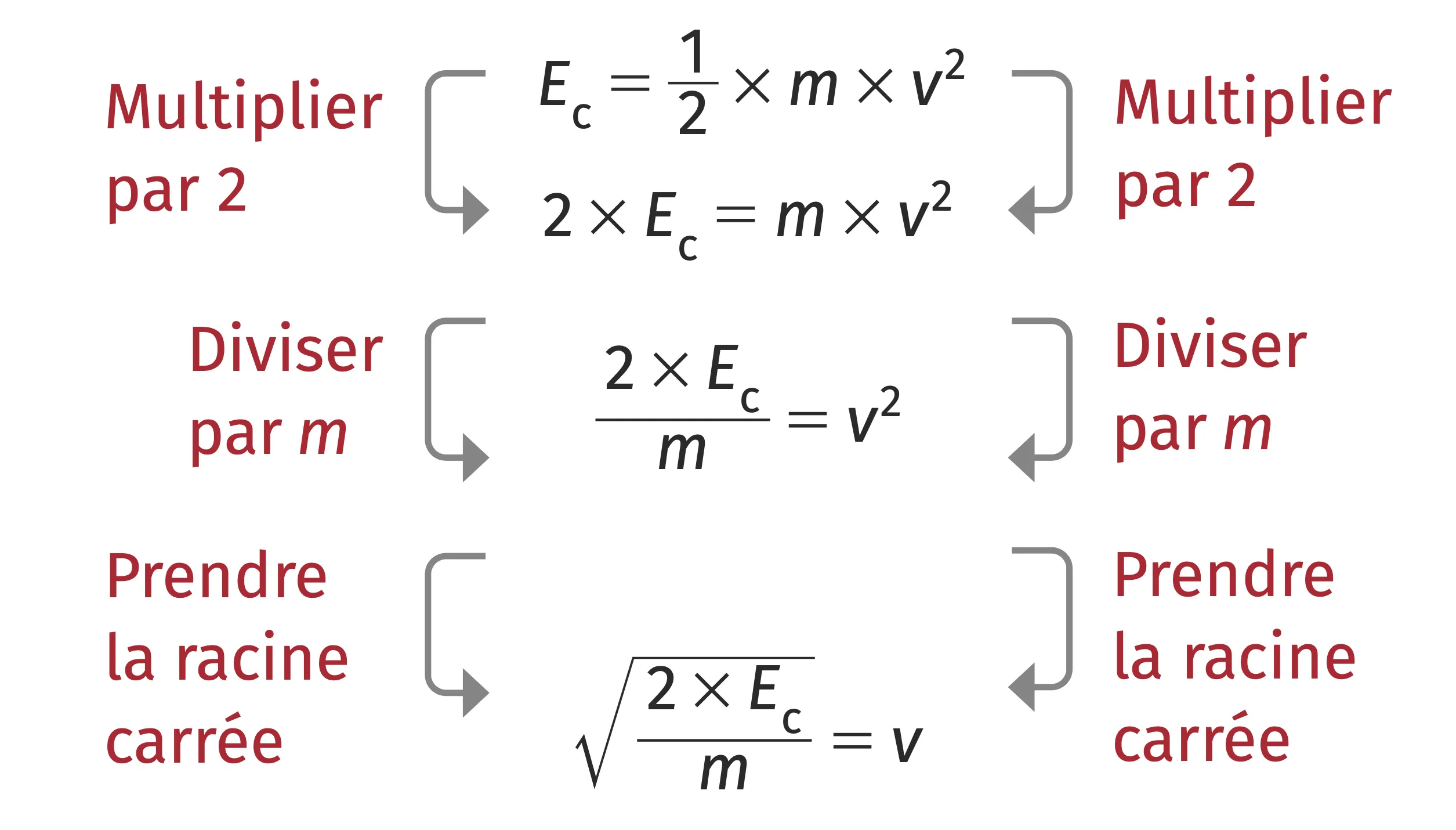


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application
1Échantillon d'acier
Un échantillon d'acier a une masse m=0,8 \mathrm{~kg}. La masse volumique de l'acier est \rho=7~860 \mathrm{~kg} / \mathrm{m}^3.
Calculer le volume V de cet échantillon d'acier.
Calculer le volume V de cet échantillon d'acier.
Aide
La relation entre la masse volumique \rho d'un objet de masse m et de volume V est :
m=\rho \times V
Il faut donc isoler le volume V.
2Consommation électrique
En moyenne, un réfrigérateur consomme quotidiennement une énergie
électrique E=1,0\:\mathrm{kWh}.
Calculer la puissance P de ce réfrigérateur en kilowatt (\mathrm{kW}).
Calculer la puissance P de ce réfrigérateur en kilowatt (\mathrm{kW}).
Aide
L'énergie électrique E consommée par un appareil est reliée à la puissance P de cet appareil et à la durée d'utilisation t par :
Il faut donc isoler P.
Ici, la durée d'utilisation est t=24 \mathrm{~h}.
E=P \times t
Il faut donc isoler P.
Ici, la durée d'utilisation est t=24 \mathrm{~h}.
3Ice Memory (extrait du DNB de métropole de 2019)
Le projet ICE MEMORY est un programme scientifique dont l'objectif est de constituer la première archive glaciaire du monde. Des carottes provenant des glaciers les plus en danger seront conservées à -54 °C dans une cave creusée sous la neige de l'Antarctique (base de Vostok).


Doc. 1Intensité de pesanteur des différents lieux de prélèvement de carottes glaciaires
| Lieu de prélèvement de carottes glaciaires | Intensité de pesanteur \bold{g} du lieu |
|---|---|
| Glacier du mont Illimani (Bolivie). Altitude : 6 300 m | g=9,76 \mathrm{~N} / \mathrm{kg} |
| Glacier du col du Dôme (France). Altitude : 4 236 m | g=9,79 \mathrm{~N} / \mathrm{kg} |
| Base de Vostok (Antarctique). Altitude : 3 800 m | g=9,82 \mathrm{~N} / \mathrm{kg} |
À l'aide des données du tableau, calculer la masse m d'un cylindre de glace en kilogramme (\mathrm{kg}) dont le poids à Vostok est égal à P = 236\:N. Expliquer la démarche suivie et écrire la relation utilisée.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
