Mathématiques Terminale Bac Pro
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 4
Avant de commencer
Fonctions polynômes de degré 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'objectif de ce chapitre est d'étudier la fonction cube et les fonctions polynômes de degré 3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Pour modéliser le tracé des rails d'une montagne russe, on peut être amené à utiliser la courbe représentative d'une fonction polynomiale de degré 3. Une telle modélisation permet au constructeur de déterminer, par exemple, l'altitude maximale atteinte par cette attraction, ou bien encore la pente à laquelle les utilisateurs seront soumis durant toute sa durée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rappels de première
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fonctions polynômes de degré 2
Une fonction polynôme \bm f de degré 2 est une fonction pour laquelle il existe trois nombres réels a, b et c, avec a \neq 0, tels que pour tout réel x, f(x)=a x^{2}+b x+c.La représentation graphique d'une fonction polynôme de degré 2 est une parabole dont le sens dépend du signe de a. Elle est tournée vers le haut si a \gt 0 et tournée vers le bas si a \lt 0.
Le signe d'une fonction polynôme de degré 2 dépend du nombre de racines de cette fonction ainsi que du signe de a.

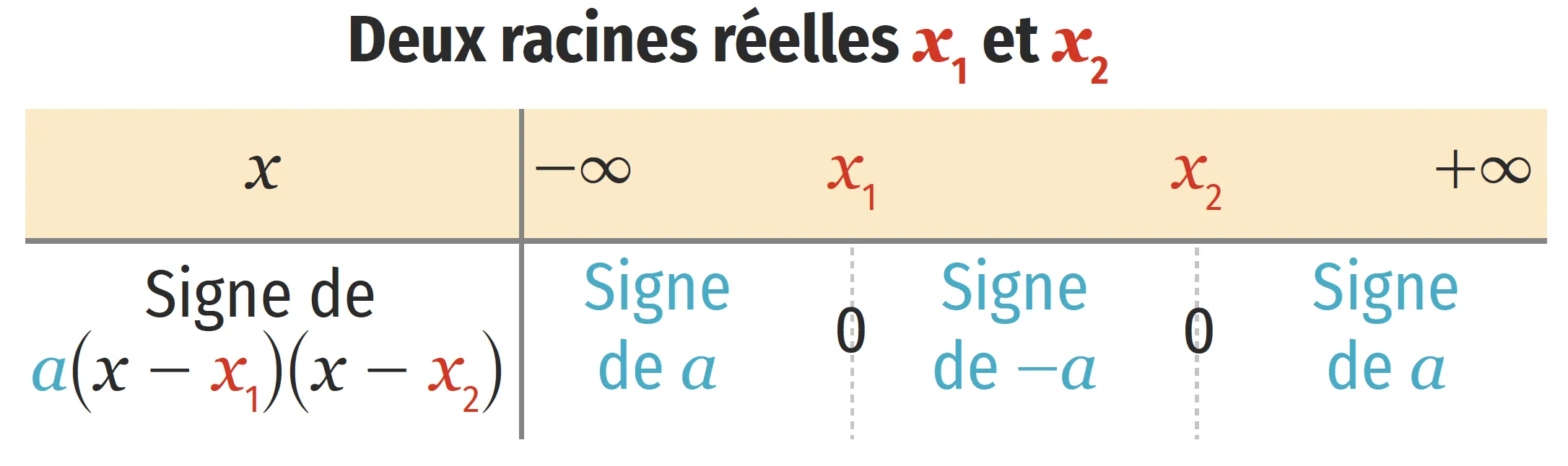

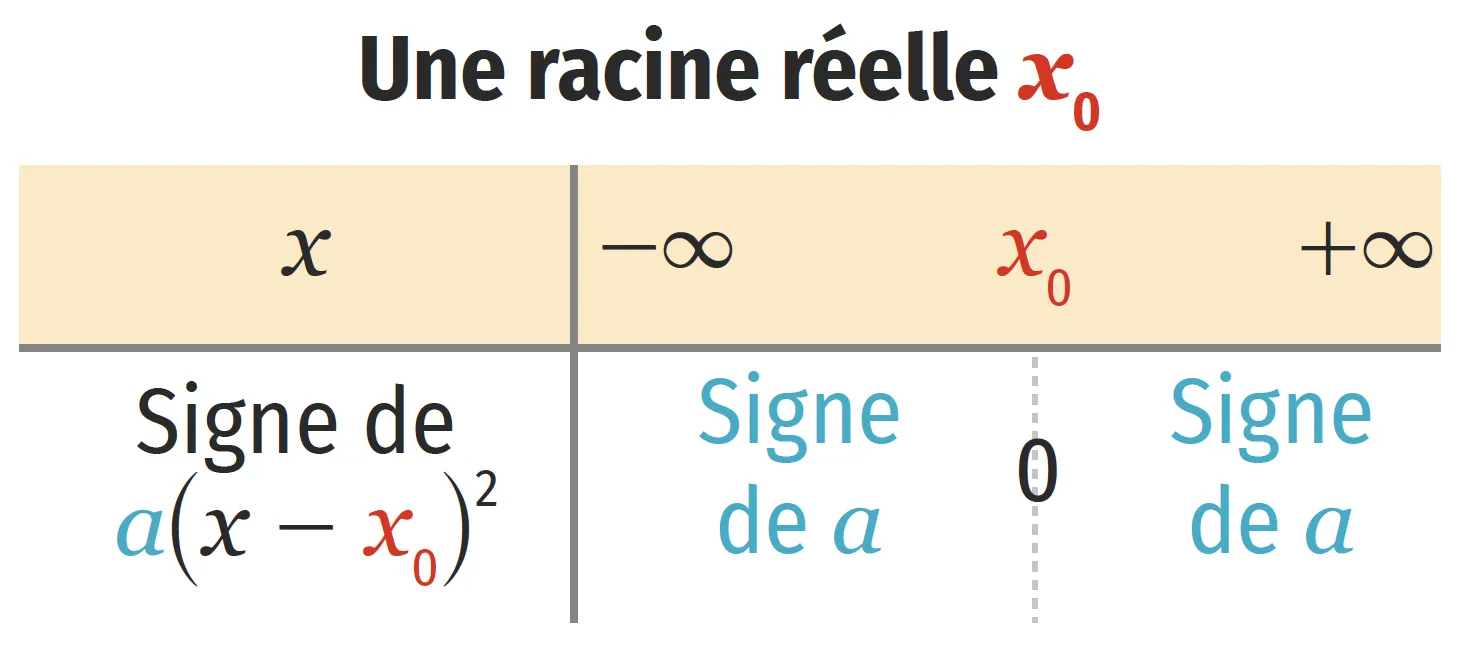
S᾽il n᾽a pas de racine réelle, un polynôme de degré 2 est du signe de a.
Tableau de fonctions dérivées




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Validation des acquis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1
Soit f la fonction définie sur \Reals par :
Sous forme factorisée, cette fonction peut s'écrire :
1. fest une fonction polynôme de :
2. Sa représentation graphique est :
3. L'équation f(x)=0 admet :
f(x)=2 x^{2}+12 x-14.
Sous forme factorisée, cette fonction peut s'écrire :
f(x)=2(x-1)(x+7).
1. fest une fonction polynôme de :
2. Sa représentation graphique est :
3. L'équation f(x)=0 admet :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2
Déterminer les fonctions dérivées des fonctions suivantes toutes définies sur \Reals.
a. f(x)=3 x
b. g(x)=-2 x+4
c. h(x)=-4 x^{2}
d. i(t)=-5 t^{2}+2 t-1
a. f(x)=3 x
b. g(x)=-2 x+4
c. h(x)=-4 x^{2}
d. i(t)=-5 t^{2}+2 t-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
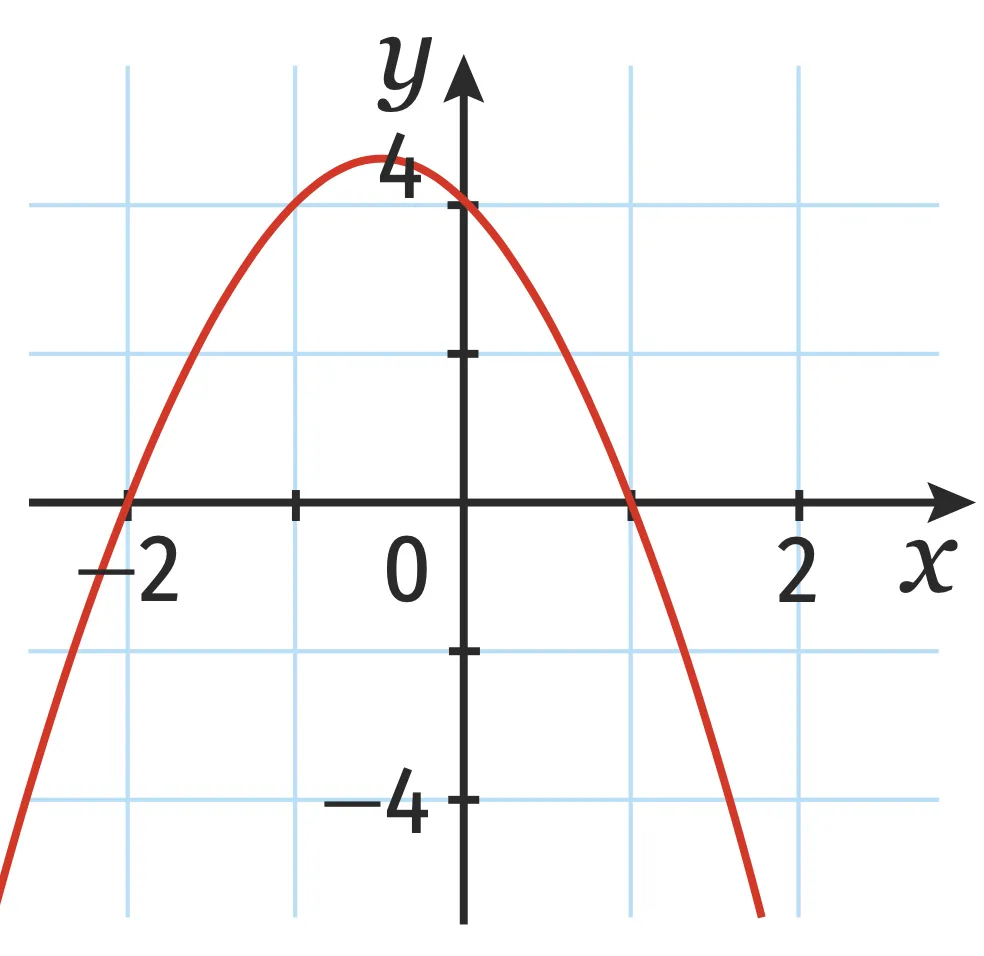
Exercice 3
Associer à chaque fonction sa représentation graphique. Justifier.
c.
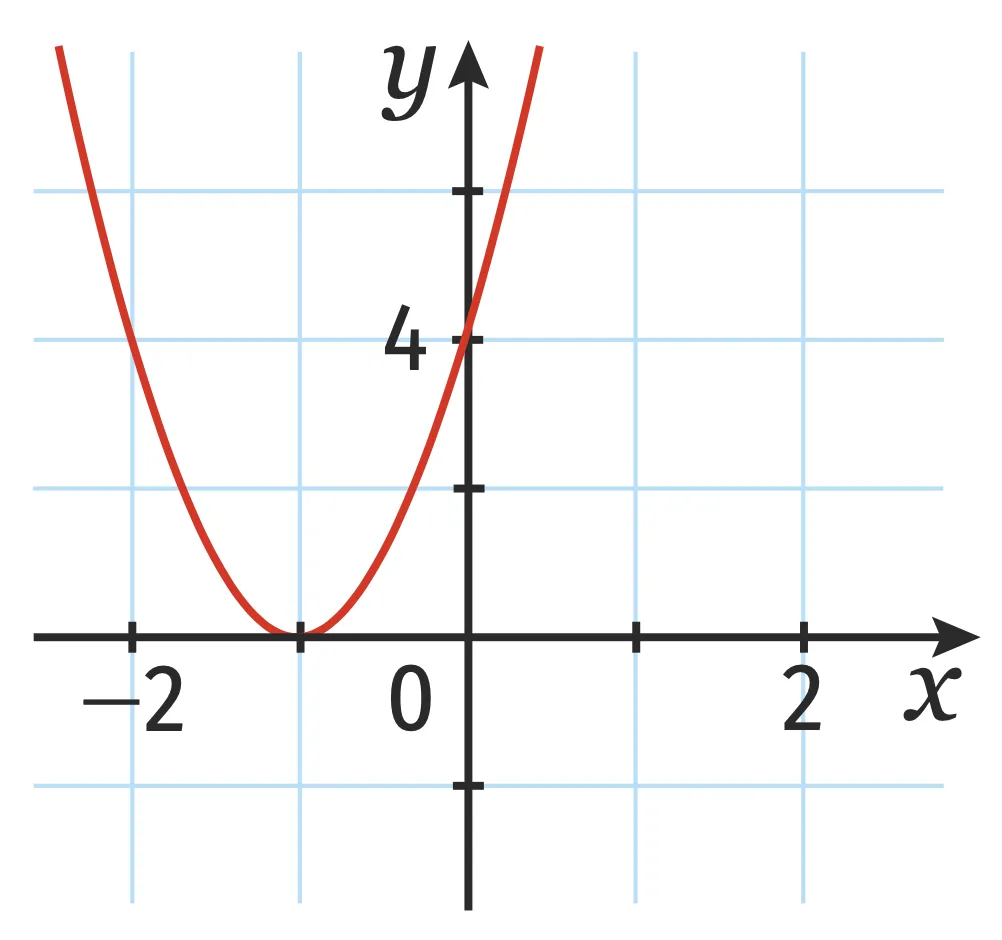
a.

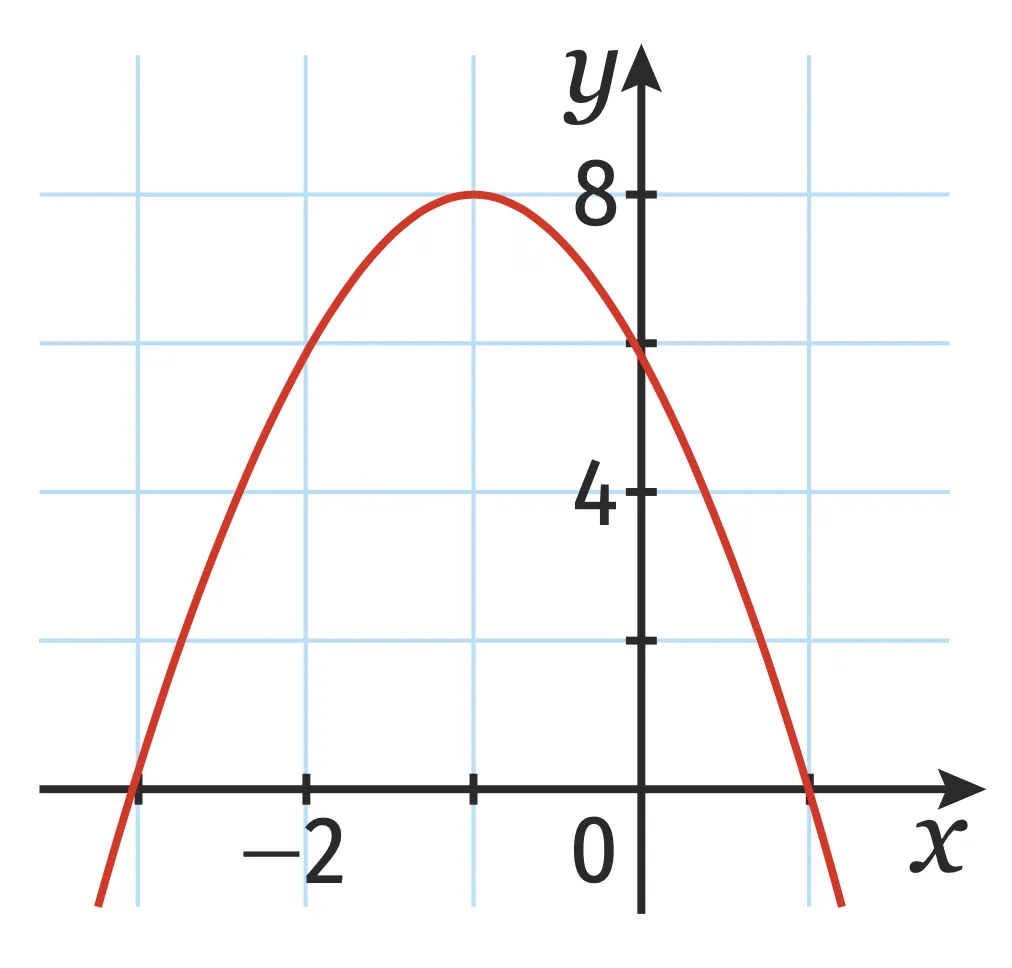


b.

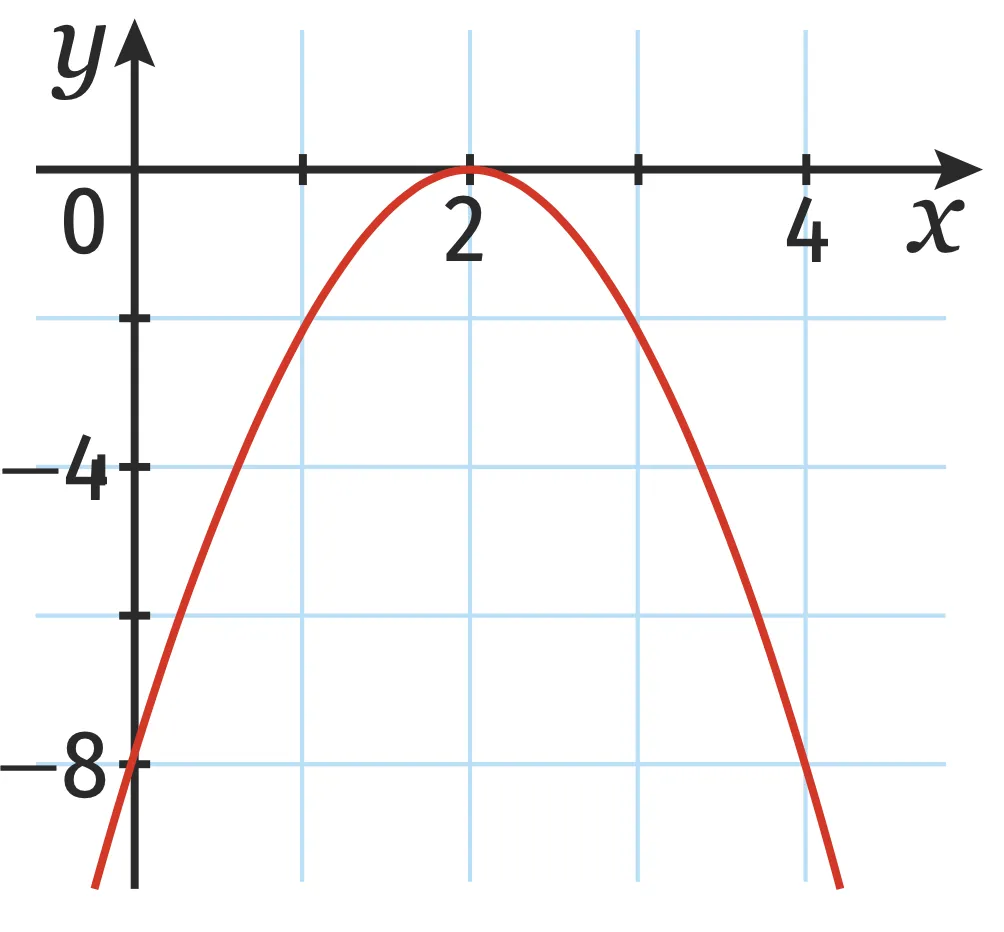


c.


d. 


Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
