Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 4
Exercices
Travailler ensemble
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Changement d'état
Chaque partie de cet exercice peut être réalisée seul(e) ou en groupe. Les élèves mettent leurs résultats en commun pour résoudre le problème.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Un changement d'état pour une espèce chimique est le passage d'un état physique à un autre. Si on refroidit suffisamment de l'eau liquide, elle passe à l'état solide (glace). Pour l'eau pure, la phase de solidification se fait à température constante (0 °C dans les conditions normales de pression). Cette transformation prend un certain temps.
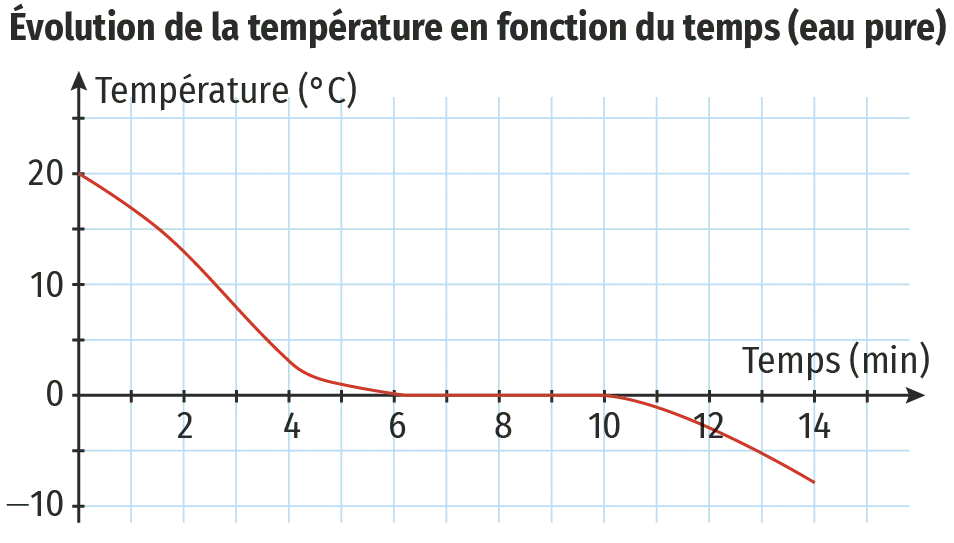
On souhaite étudier la courbe de température de la solidification de l'eau salée ainsi que la vitesse de cette transformation.
Elle peut être modélisée par la fonction f définie par f(t)=-0,9 t^{3}+8 t^{2}-24,4 t+20, où t représente le temps en minute et f(t) la température du mélange en degré Celsius.
Le zoom est accessible dans la version Premium.
On souhaite étudier la courbe de température de la solidification de l'eau salée ainsi que la vitesse de cette transformation.
Elle peut être modélisée par la fonction f définie par f(t)=-0,9 t^{3}+8 t^{2}-24,4 t+20, où t représente le temps en minute et f(t) la température du mélange en degré Celsius.
Problématique
La solidification de l'eau salée se fait-elle à température constante ?
À quel moment l'évolution de la température est-elle la plus lente ?
À quel moment l'évolution de la température est-elle la plus lente ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 1
Étude de la fonction f définie sur [0\:;5] par :
1. Tracer la courbe représentative de la fonction f.
2. Tracer la courbe représentative de la fonction dérivée f' et étudier son signe.
3. Dresser le tableau de variations de la fonction f.
4. Pour l'eau salée, la phase de solidification se fait-elle à température constante ?
f(x)=-0,9 x^{3}+8 x^{2}-24,4 x+20.
1. Tracer la courbe représentative de la fonction f.
GeoGebra
2. Tracer la courbe représentative de la fonction dérivée f' et étudier son signe.
GeoGebra
3. Dresser le tableau de variations de la fonction f.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
4. Pour l'eau salée, la phase de solidification se fait-elle à température constante ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 2
Étude de la fonction g définie sur [0\:;5] par :
1. Donner l'expression de la fonction dérivée g'.
2. Résoudre, à l᾽unité près, l᾽équation g'(x) = 0.
3. Dresser le tableau de signe de la fonction g'.
4. Dresser le tableau de variations de la fonction g.
g(x)=-2,7 x^{2}+16 x-24,4
1. Donner l'expression de la fonction dérivée g'.
2. Résoudre, à l᾽unité près, l᾽équation g'(x) = 0.
3. Dresser le tableau de signe de la fonction g'.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
4. Dresser le tableau de variations de la fonction g.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 3
Recherches Internet :
1. Qu'est-ce qu'un point d'inflexion ?
2. Comment peut-on le repérer sur une courbe ?
3. Comment faire le lien entre le point d'inflexion, la tangente à la courbe en ce point et la vitesse de la transformation ?
1. Qu'est-ce qu'un point d'inflexion ?
2. Comment peut-on le repérer sur une courbe ?
3. Comment faire le lien entre le point d'inflexion, la tangente à la courbe en ce point et la vitesse de la transformation ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah