Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 4
Activité C
Volume du bassin
Capacités : Dresser le tableau de variations d'une fonction polynôme de degré inférieur ou égal à 3 et l᾽exploiter pour déterminer le nombre de solutions de l'équation f(x)=c, où c est un nombre réel.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
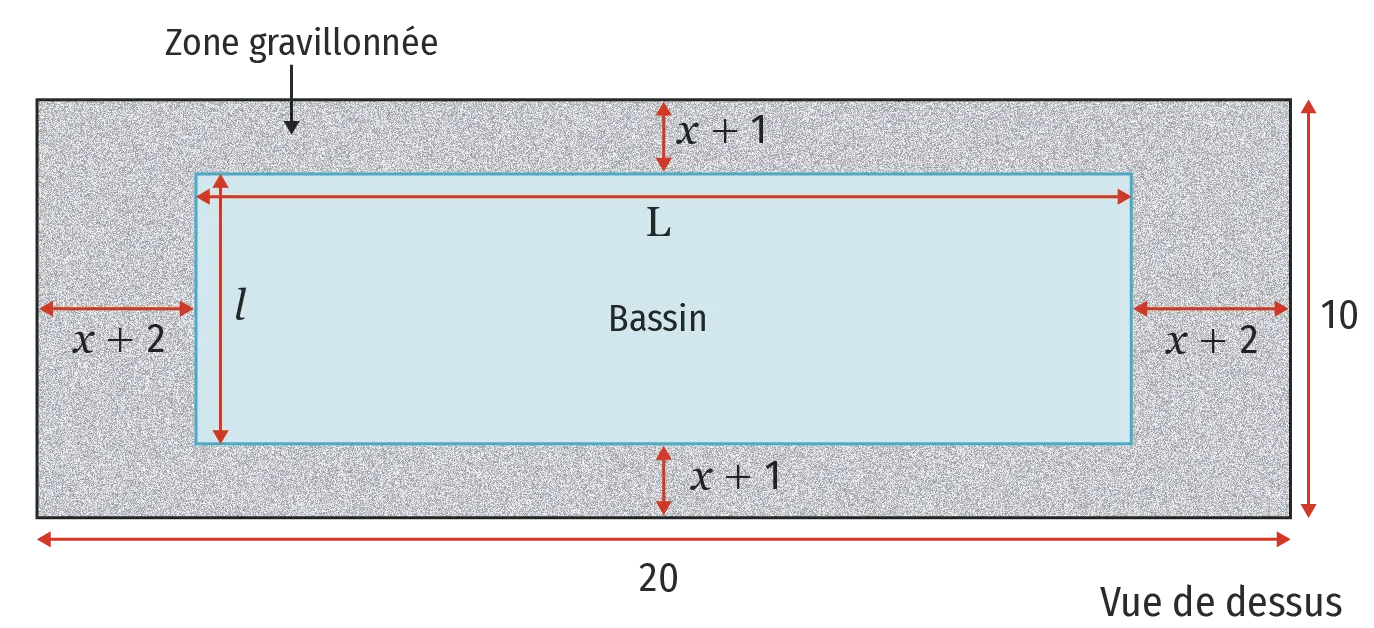
Carole désire construire dans son jardin un bassin en forme de pavé droit d'un volume de 50 m3 pour ses nénuphars. Afin de pouvoir circuler autour, elle prévoit une zone gravillonnée représentée sur le schéma ci-dessous. Les cotes sont exprimées en mètre.
Problématique
Quelles sont les dimensions (longueur, largeur et profondeur) du bassin ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
a. S'approprier
Exprimer la longueur \text{L} du bassin en fonction de x.
b. S'approprier Exprimer la largeur l du bassin en fonction de x.
c. S'approprier En déduire l'expression de l'aire de la surface du bassin en fonction de x.
b. S'approprier Exprimer la largeur l du bassin en fonction de x.
c. S'approprier En déduire l'expression de l'aire de la surface du bassin en fonction de x.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Valider
Justifier que l'on doit forcément avoir 0 \leqslant x \leqslant 3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
a. Réaliser, valider
Montrer que l'expression du volume v du bassin en fonction de x est :
b. Réaliser
En déduire l'expression de la fonction dérivée v'.
Montrer que l'expression du volume v du bassin en fonction de x est :
v(x)=-4 x^{3}+60 x^{2}-272 x+384.
b. Réaliser
En déduire l'expression de la fonction dérivée v'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
a. Réaliser
En sachant que les solutions, arrondies au dixième, de l᾽équation v^{\prime}(x)=0 sont x_{1} \approx 3,5 et x_{2} \approx 6,5, dresser le tableau de signe de v'(x) sur l'intervalle [0 \:; 8].
b. Réaliser En déduire le tableau de variations de la fonction v.
c. Réaliser En déduire le nombre de solutions de l'équation v(x)=50. Justifier.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
b. Réaliser En déduire le tableau de variations de la fonction v.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
c. Réaliser En déduire le nombre de solutions de l'équation v(x)=50. Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Valider
Tracer la fonction v à l᾽aide d᾽un outil numérique.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Communiquer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Soit f une fonction continue strictement monotone sur [\textit{a} \:; \textit{b}] et c un nombre compris entre f(a) et f(b). Alors, l'équation f(x)=c admet une solution unique sur [\textit{a} \:; \textit{b}].
Pour s᾽entraîner :
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah