Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 4
Applications
Fonctions polynômes de degré 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer la dérivée d'une fonction polynôme de degré inférieur ou égal à 3
| f | f' |
|---|---|
| f(x)=a | f'(x)=0 |
| f(x)=x | f'(x)=1 |
| f(x)=x^2 | f'(x)=2x |
| f(x)=x^3 | f'(x)=3x^2 |
1. Dériver le terme en x^3, le terme en x^2, le terme en x et le terme constant en utilisant le tableau de dérivées ci-dessus et la formule (k \times f)^{\prime}=k \times f^{\prime}.
2. Déterminer la dérivée de la fonction en utilisant le fait que la dérivée d'une somme est la somme des dérivées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exploiter le tableau de variations d'une fonction polynôme de degré inférieur ou égal à 3
-
Déterminer le nombre de solutions de l'équation f(x)=k.
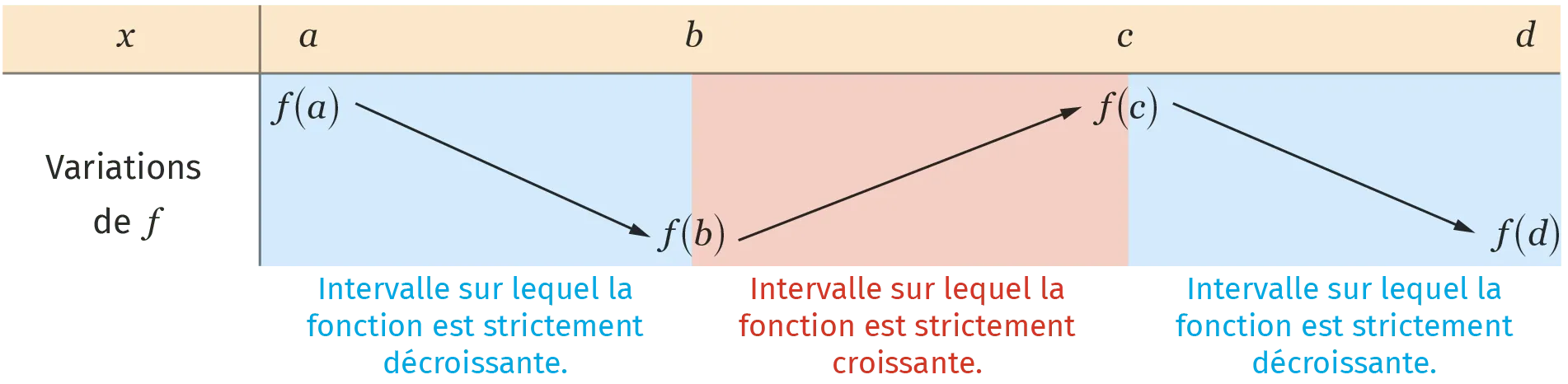
1. Se placer sur un intervalle où la fonction est monotone, c'est-à-dire soit strictement croissante, soit strictement décroissante.
2. Regarder la valeur maximale et la valeur minimale prises par la fonction sur cet intervalle. Si k se trouve entre ces deux valeurs, l'équation admet une solution sur cet intervalle. Sinon, il n'existe pas de solution sur cet intervalle.
3. Recommencer ce processus sur tous les intervalles sur lesquels la fonction est soit strictement croissante, soit strictement décroissante. Compter le nombre de solutions ainsi obtenues.
Le zoom est accessible dans la version Premium.
-
Déterminer les extremums locaux d'une fonction f.
D'après le tableau de variations ci-dessus, on peut dire que :- sur l'intervalle ] a\:; c[, f(b) est un minimum local ;
- sur l'intervalle ] b\:; d[, f(c) est un maximum local.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dresser le tableau de variations d'une fonction polynôme de degré inférieur ou égal à 3
1. Déterminer l'expression de la fonction dérivée f'.
2. Chercher les racines de la fonction dérivée à l'aide d'un outil numérique.
3. Dresser le tableau de signe de la fonction dérivée.
4. Dresser le tableau de variations de la fonction f : lorsque sa dérivée est positive, la fonction est croissante et lorsque sa dérivée est négative, la fonction est décroissante.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Mise en pratique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCM
Une ou plusieurs bonnes réponses possibles.
1. Soit f une fonction polynôme de degré 3.
La fonction dérivée de f est une fonction polynôme de degré :
2. Soit k la fonction polynôme définie sur \Reals par k(x)=(x+2)(x+3)(x-1).
La fonction k est une fonction polynôme de degré :
3. Soit g la fonction polynôme de degré 3 définie sur \Reals par g(x)=\frac{2}{3} x^{3}-2 x^{2}-6 x+1. Alors :
4. L'équation x^{3}+2 x^{2}-3 x=0 admet pour solution :
La fonction dérivée de f est une fonction polynôme de degré :
2. Soit k la fonction polynôme définie sur \Reals par k(x)=(x+2)(x+3)(x-1).
La fonction k est une fonction polynôme de degré :
3. Soit g la fonction polynôme de degré 3 définie sur \Reals par g(x)=\frac{2}{3} x^{3}-2 x^{2}-6 x+1. Alors :
4. L'équation x^{3}+2 x^{2}-3 x=0 admet pour solution :
Dans les questions 5. à 7. , on s'intéresse à la fonction polynôme de degré 3 nommée h dont le tableau de variations est le suivant.
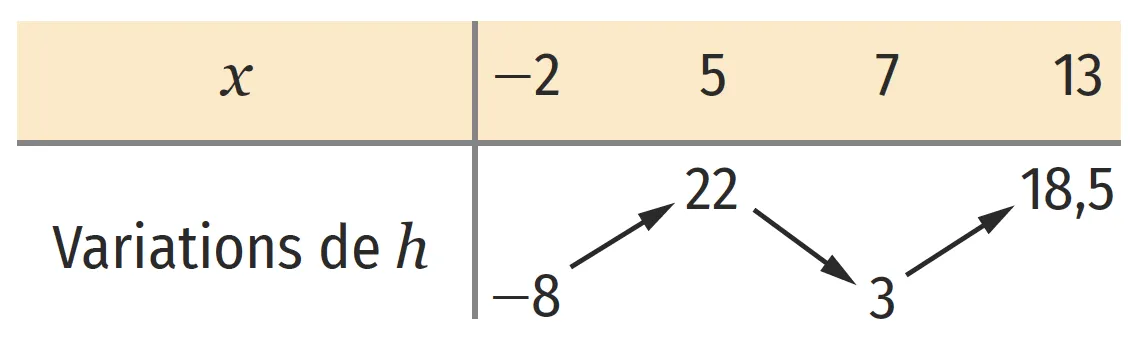5. Sur l᾽intervalle [-2\:; 13], la fonction dérivée h' de la fonction h admet :
6. Sur l᾽intervalle ] 5\:; 13[, la fonction h admet un minimum local en :
7. Sur l᾽intervalle [-2\:; 13], l᾽équation h(x)=0 admet :
Le zoom est accessible dans la version Premium.
6. Sur l᾽intervalle ] 5\:; 13[, la fonction h admet un minimum local en :
7. Sur l᾽intervalle [-2\:; 13], l᾽équation h(x)=0 admet :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème
Soit la fonction f définie sur [-4\:; 4] par f(x)=2 x^{3}-3 x^{2}-12 x+2.
1. Déterminer l'expression de f', fonction dérivée de la fonction f.
2. Montrer que f^{\prime}(-1)=0 et f^{\prime}(2)=0.
3. La fonction f' peut se mettre sous la forme a\left(x-x_{1}\right)\left(x-x_{2}\right). Donner les valeurs de a, x_1 et x_2.
4. Dresser le tableau de signe de la fonction f' sur [-4\:; 4].
5. Dresser le tableau de variations de la fonction f sur [-4\:; 4].
6. En déduire le nombre de solutions de l'équation f(x)=5 sur [-4 \:; 4].
7. Donner les coordonnées des extremums locaux de la fonction f sur ]-4\:; 4[.
1. Déterminer l'expression de f', fonction dérivée de la fonction f.
2. Montrer que f^{\prime}(-1)=0 et f^{\prime}(2)=0.
3. La fonction f' peut se mettre sous la forme a\left(x-x_{1}\right)\left(x-x_{2}\right). Donner les valeurs de a, x_1 et x_2.
4. Dresser le tableau de signe de la fonction f' sur [-4\:; 4].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
5. Dresser le tableau de variations de la fonction f sur [-4\:; 4].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
6. En déduire le nombre de solutions de l'équation f(x)=5 sur [-4 \:; 4].
7. Donner les coordonnées des extremums locaux de la fonction f sur ]-4\:; 4[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Réviser les notions de ce chapitre grâce à cette activité interactive.
Pour une utilisation optimale, réaliser l'activité en plein écran.
Genially
Pour une utilisation optimale, réaliser l'activité en plein écran.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah