Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 4
Activité A
Déménagement
Capacité : Étudier la fonction cube.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour son déménagement, Thomas a loué un camion.
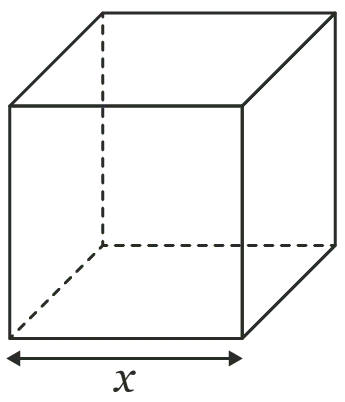
Après quelques heures de chargement, le camion est pratiquement rempli. Il reste cependant un peu d'espace que Thomas souhaite combler avant d'effectuer le trajet jusqu'à sa nouvelle maison. L'espace disponible est de forme cubique. Thomas estime qu'il pourrait contenir jusqu'à 7 m3.
Thomas dispose de plusieurs tailles de cartons, tous de forme cubique. Il cherche à savoir quelle taille de carton il doit utiliser pour remplir au mieux cet espace.
Après quelques heures de chargement, le camion est pratiquement rempli. Il reste cependant un peu d'espace que Thomas souhaite combler avant d'effectuer le trajet jusqu'à sa nouvelle maison. L'espace disponible est de forme cubique. Thomas estime qu'il pourrait contenir jusqu'à 7 m3.
Thomas dispose de plusieurs tailles de cartons, tous de forme cubique. Il cherche à savoir quelle taille de carton il doit utiliser pour remplir au mieux cet espace.
Problématique
Quelle taille de carton Thomas doit-il choisir pour combler cet espace libre ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1S'approprier
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Réaliser
Compléter le tableau de valeurs ci-dessous.
| Longueur x de l'arête (en m) | 0,5 | 1 | 1,5 | 2 |
| Volume \text{V} du carton (en m3) |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
a. Analyser/raisonner
Thomas peut-il choisir un carton dont les arêtes mesurent 2 m ? Justifier.
b. Réaliser Tracer la représentation graphique du volume \text{V} d'un carton en fonction de x, la longueur de l'arête de ce carton.
Thomas peut-il choisir un carton dont les arêtes mesurent 2 m ? Justifier.
b. Réaliser Tracer la représentation graphique du volume \text{V} d'un carton en fonction de x, la longueur de l'arête de ce carton.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Analyser / Raisonner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Analyser / Raisonner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
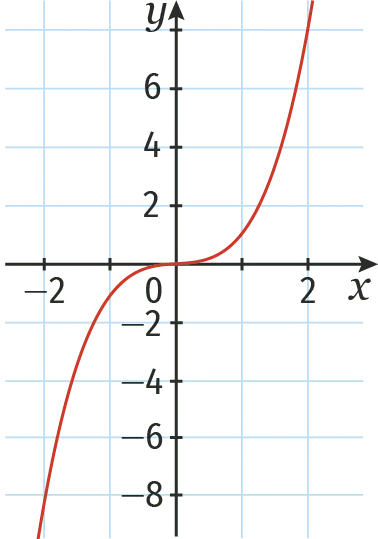
- La fonction cube est la fonction f qui, à tout réel x, associe son cube.
- Elle est définie par f(x)=x^{3}.
- Cette fonction est strictement croissante sur \Reals.
- Sa représentation graphique est donnée ci-dessous.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah