Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 9
Entraînement 1
Nombre dérivé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On rappelle que :
- la vitesse instantanée correspond à la dérivée de la position par rapport au temps ;
- l'accélération instantanée correspond à la dérivée de la vitesse par rapport au temps.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 52
[Raisonner.]
On s'intéresse à la trajectoire d'un point dont la position f(t), en mètre, en fonction du temps t, en minute, est modélisée par la fonction f définie par f(t)=-3 t^{2}+13 t+1.
1. Exprimer la vitesse instantanée du point en fonction du temps.
2. Quelle est la vitesse du point au bout d'une minute ?
3. Déterminer l'accélération instantanée du point en fonction du temps. Que constate-t-on ?
1. Exprimer la vitesse instantanée du point en fonction du temps.
2. Quelle est la vitesse du point au bout d'une minute ?
3. Déterminer l'accélération instantanée du point en fonction du temps. Que constate-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 53
[Raisonner.]
On s'intéresse au nombre de bactéries dans un milieu de culture fermé. Ce nombre f(t), exprimé en centaine, varie en fonction du temps t, en minute, en suivant l'expression f(t)=4+6 t+5 t^{2} sur l'intervalle [0\,; 5].
1. Exprimer la vitesse instantanée de croissance du nombre de bactéries en fonction du temps.
2. Quelle est la vitesse de croissance du nombre de bactéries au bout de 4 minutes ?
3. Déterminer l'accélération instantanée de la croissance du nombre de bactéries en fonction du temps.
1. Exprimer la vitesse instantanée de croissance du nombre de bactéries en fonction du temps.
2. Quelle est la vitesse de croissance du nombre de bactéries au bout de 4 minutes ?
3. Déterminer l'accélération instantanée de la croissance du nombre de bactéries en fonction du temps.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 54
[Raisonner.]
On s'intéresse à une onde de longueur d'onde m. Sa longueur d'onde est reliée à la vitesse de propagation c et la fréquence f par la relation \lambda=\frac{c}{f}.
1. Exprimer la dérivée \frac{\mathrm{d} \lambda}{\mathrm{d} c}.
2. Exprimer la dérivée \frac{\mathrm{d} \lambda}{\mathrm{d} f}.
1. Exprimer la dérivée \frac{\mathrm{d} \lambda}{\mathrm{d} c}.
2. Exprimer la dérivée \frac{\mathrm{d} \lambda}{\mathrm{d} f}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 55
[Raisonner.]
En électricité, la loi d'Ohm permet de calculer la résistance \text{R} d'un dipôle en ohm, à partir de la tension \text{U} à ses bornes, exprimée en volt, et de l'intensité \text{I} du courant, exprimée en ampère, à l'aide de la relation suivante : \mathrm{R}=\frac{\mathrm{U}}{\mathrm{I}}.
1. Exprimer la dérivée \frac{\mathrm{dR}}{\mathrm{d} \mathrm{U}} .
2. Exprimer la dérivée \frac{\mathrm{dR}}{\mathrm{dI}}.
1. Exprimer la dérivée \frac{\mathrm{dR}}{\mathrm{d} \mathrm{U}} .
2. Exprimer la dérivée \frac{\mathrm{dR}}{\mathrm{dI}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans la vie professionnelle
Un acousticien, spécialiste de la propagation du son, a pour objectif de mesurer et classifier les nuisances sonores. Lors d'une intervention, après avoir établi un diagnostic, il propose une solution en respectant un cahier des charges précis. Il peut également être sollicité en amont dès la phase de conception d'une machine, voie de transport ou salle de spectacle. Polyvalent et formé aux nouvelles technologies, l'acousticien est un artisan de notre confort sonore au quotidien.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
La notation \left(\frac{\mathrm{d} y}{\mathrm{~d} x}\right)_{x_{\text{A}}} ou \left(\frac{\mathrm{d} f}{\mathrm{~d} x}\right)_{x_{\text{A}}} est due à l'Allemand Gottfried Wilhelm Leibniz (1646-1716), considéré comme le dernier « génie universel » dont le champ de compétence comprenait, entre autres, la philosophie, le droit et les sciences.
On lui doit en particulier la normalisation des mots « fonctions » et « coordonnées », mais aussi des symboles « : » pour la division, « • » pour la multiplication et la notation « y=f(x) » pour les fonctions.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 56
[Raisonner.]
Pour un exposé de sciences, Élise et Marianne veulent étudier l'évolution d'une population de drosophiles.
Au jour 0, elles déposent 10 drosophiles dans une boîte fermée contenant de la nourriture et, tous les jours, elles comptent les insectes.
Leur camarade Thierry construit la courbe C_{f} montrant l'évolution de l'effectif \text{E} des drosophiles en fonction du temps t en jour.
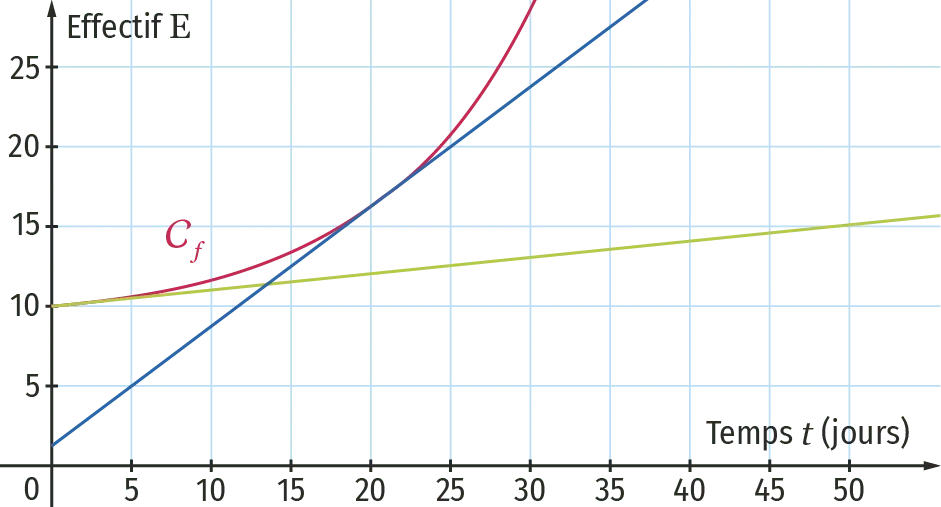
Il ajoute sur le graphique les tangentes à la courbe aux points d'abscisses 0 et 20.
Déterminer graphiquement la vitesse instantanée de l'évolution de l'effectif des drosophiles au jour 0 et au jour 20.
Au jour 0, elles déposent 10 drosophiles dans une boîte fermée contenant de la nourriture et, tous les jours, elles comptent les insectes.
Leur camarade Thierry construit la courbe C_{f} montrant l'évolution de l'effectif \text{E} des drosophiles en fonction du temps t en jour.
Le zoom est accessible dans la version Premium.
Il ajoute sur le graphique les tangentes à la courbe aux points d'abscisses 0 et 20.
Déterminer graphiquement la vitesse instantanée de l'évolution de l'effectif des drosophiles au jour 0 et au jour 20.
Aide
La vitesse instantanée de l'évolution à l'instant t_{0} est \left(\frac{\mathrm{dE}}{\mathrm{d} t}\right)_{t_0}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 57
[Communiquer.]
À l'hôpital, un patient prend un médicament. Les infirmiers mesurent la concentration de ce médicament dans son sang à chaque instant.
On a tracé ci-dessous la courbe de cette concentration, en milligramme par litre, en fonction du temps en minute.
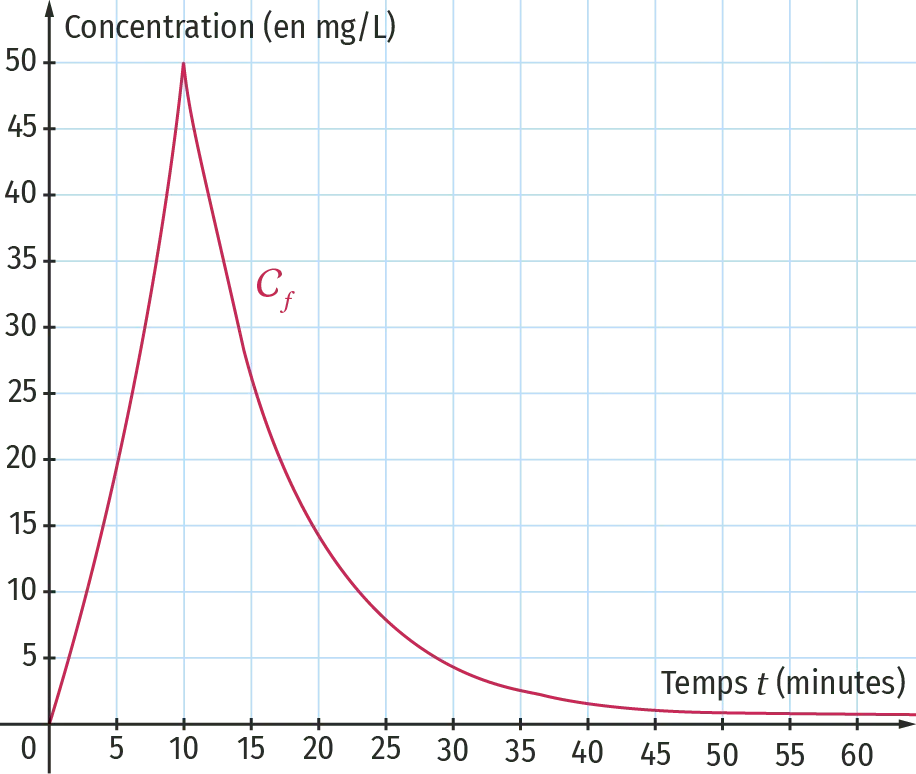
À l'aide de la courbe, justifier à quel instant la vitesse d'absorption du médicament est la plus élevée.
On a tracé ci-dessous la courbe de cette concentration, en milligramme par litre, en fonction du temps en minute.
Le zoom est accessible dans la version Premium.
À l'aide de la courbe, justifier à quel instant la vitesse d'absorption du médicament est la plus élevée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans la vie professionnelle
Le technicien de laboratoire, travaillant dans un institut ou laboratoire, effectue des analyses biologiques ou prépare des expériences. Avec de solides compétences théoriques en chimie et biologie, ainsi que pratiques avec le matériel de laboratoire, il est capable de suivre un produit lors de sa fabrication ou encore de confirmer ou infirmer un diagnostic médical. C'est une profession qui nécessite minutie et rigueur : une conclusion erronée peut avoir de graves conséquences.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 58
[Calculer.]
Cédric a couru en 2017 le marathon de Paris. Sa montre connectée a récolté des données pendant sa course. Il a obtenu le tableau suivant.
La vitesse moyenne entre deux instants correspond au taux de variation v=\frac{\Delta d}{\Delta t}.
1. Calculer les vitesses moyennes entre chaque collecte de données.
2. À quel moment a-t-il été le plus performant ? Le moins performant ?
3. Au final, il a fini le marathon de 42,195 km en 4 h 20. Quelle a été sa vitesse moyenne sur l'ensemble du parcours ?
Le zoom est accessible dans la version Premium.
| Distance d (km) | 0 | 5 | 12 | 18 | 25 | 34 | 40 |
|---|---|---|---|---|---|---|---|
| Temps t (minutes) | 0 | 27 | 70 | 105 | 150 | 206 | 245 |
La vitesse moyenne entre deux instants correspond au taux de variation v=\frac{\Delta d}{\Delta t}.
1. Calculer les vitesses moyennes entre chaque collecte de données.
2. À quel moment a-t-il été le plus performant ? Le moins performant ?
3. Au final, il a fini le marathon de 42,195 km en 4 h 20. Quelle a été sa vitesse moyenne sur l'ensemble du parcours ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 59
Tableur
[Calculer.]
On a relevé les données dans une feuille de calcul d'une simulation du développement d'une bactérie en milieu fermé.
Quelle formule doit-on écrire dans la cellule C3, puis étirer vers la droite, pour que le tableur calcule le taux de variation de l'évolution \frac{\Delta \mathrm{E}}{\Delta t} entre deux relevés consécutifs ?
Le zoom est accessible dans la version Premium.
Quelle formule doit-on écrire dans la cellule C3, puis étirer vers la droite, pour que le tableur calcule le taux de variation de l'évolution \frac{\Delta \mathrm{E}}{\Delta t} entre deux relevés consécutifs ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 60
[Calculer.]
On s'intéresse à l'oxydation de l'ammoniac : en se consumant
dans l'oxygène, il se forme de l'eau et du diazote.
L'équation stoechiométrique de la réaction peut s'écrire
L'ammoniac disparaît à une vitesse de \text{0,1} mol/L·s.
1. Quelle est la vitesse volumique de la réaction ?
2. Quelle est la vitesse de disparition du dioxygène ?
3. Quelle est la vitesse d'apparition de l'eau et du diazote ?
4 \mathrm{NH}_{3}+3 \mathrm{O}_{2} \rightarrow 2 \mathrm{~N}_{2}+6 \mathrm{H}_{2} \mathrm{O}.
On admet que la vitesse volumique d'une réaction, notée v(t) et exprimée en mol/L·s, est calculée à l'aide de la formule
v(t)=\frac{1}{\nu_{k}} \times \frac{\mathrm{d}\left[\mathrm{C}_{k}\right]}{\mathrm{d} t}
où \left[\mathrm{C}_{k}\right] désigne la concentration de l'espèce k, exprimée en mol/L, et \nu_{k} son coefficient stoechiométrique.L'ammoniac disparaît à une vitesse de \text{0,1} mol/L·s.
1. Quelle est la vitesse volumique de la réaction ?
2. Quelle est la vitesse de disparition du dioxygène ?
3. Quelle est la vitesse d'apparition de l'eau et du diazote ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 61
Démo
[Calculer.]
On considère la fonction inverse f définie
et dérivable sur \mathbb{R} \backslash\{0\}, par f(x)=\frac{1}{x}.
1. Exprimer, en fonction de x et de h, le taux de variation de f en x non nul, c'est-à-dire \frac{f(x+h)-f(x)}{h}.
2. En faisant tendre h vers 0, conclure quant à l'expression de la dérivée de la fonction inverse.
1. Exprimer, en fonction de x et de h, le taux de variation de f en x non nul, c'est-à-dire \frac{f(x+h)-f(x)}{h}.
2. En faisant tendre h vers 0, conclure quant à l'expression de la dérivée de la fonction inverse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 62
[Calculer.]
1.
Exprimer en fonction de x et de a l'approximation affine correspondant à la fonction inverse.
2. Utiliser la formule et un entier judicieusement choisi pour calculer une valeur approchée de l'inverse de \text{0,99}.
2. Utiliser la formule et un entier judicieusement choisi pour calculer une valeur approchée de l'inverse de \text{0,99}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 63
[Calculer.]
1.
Exprimer en fonction de x et de a l'approximation affine correspondant à la fonction cosinus.
2. Utiliser la formule et une valeur remarquable du cosinus pour calculer une valeur approchée du cosinus de \frac{\pi+1}{2}.
2. Utiliser la formule et une valeur remarquable du cosinus pour calculer une valeur approchée du cosinus de \frac{\pi+1}{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 64
[Calculer.]
1.
Exprimer en fonction de x et de a l'approximation affine correspondant à la fonction sinus.
2. Utiliser la formule et une valeur remarquable du sinus pour calculer une valeur approchée du sinus de {\frac{\pi}{2}+0,1}.
2. Utiliser la formule et une valeur remarquable du sinus pour calculer une valeur approchée du sinus de {\frac{\pi}{2}+0,1}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 65
[Calculer.]
1.
Exprimer en fonction de x et de x_{\mathrm{A}} l'approximation affine correspondant à la fonction cosinus.
2. Utiliser la formule et une valeur remarquable du cosinus pour calculer une valeur approchée du cosinus de \frac{5 \pi+1}{3}.
2. Utiliser la formule et une valeur remarquable du cosinus pour calculer une valeur approchée du cosinus de \frac{5 \pi+1}{3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 66
[Calculer.]
1.
Exprimer en fonction de x et de a l'approximation affine correspondant à la fonction sinus.
2. Utiliser la formule et une valeur remarquable du sinus pour calculer une valeur approchée du sinus de \frac{-3 \pi-1}{4}.
2. Utiliser la formule et une valeur remarquable du sinus pour calculer une valeur approchée du sinus de \frac{-3 \pi-1}{4}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 67
[Chercher.]
On considère la fonction f définie pour tout réel x par :
f(x)=-\cos \left(\frac{\pi}{4}-2 x\right).
Déterminer les abscisses de deux points distincts de la courbe représentative de f pour lesquels la tangente a pour coefficient directeur 2.
Aide
On admet que, pour tout x \in \mathbb{R}:
f^{\prime}(x)=-2 \sin \left(\frac{\pi}{4}-2 x\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 68
[Chercher.]
On considère la fonction f définie pour tout réel x par :
f(x)=2 \sin \left(3 x+\frac{\pi}{2}\right).
Déterminer les abscisses de deux points distincts de
la courbe représentative de f pour lesquels la tangente
a pour coefficient directeur 3 \sqrt{3}.
Aide
On admet que, pour tout x \in \mathbb{R} :
f^{\prime}(x)=6 \cos \left(3 x+\frac{\pi}{2}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'approximation affine est également appelée approximation polynomiale d'ordre 1.
Si f est une fonction dérivable deux fois sur un intervalle \text{I} et pour a et x dans \text{I}, alors :
lorsque x est proche de a. Il s'agit alors de l'approximation polynomiale d'ordre 2 (voir ).
Si f est une fonction dérivable deux fois sur un intervalle \text{I} et pour a et x dans \text{I}, alors :
f(x) \approx f(a)+f^{\prime}(a)(x-a)+f^{\prime \prime}(a) \frac{(x-a)^{2}}{2}
lorsque x est proche de a. Il s'agit alors de l'approximation polynomiale d'ordre 2 (voir ).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 69
Exercice inversé
Dans un repère orthonormé, on considère deux
points \text{A} et \text{B}. Le taux d'accroissement entre les deux points est de \text{-8}.
Sachant que \mathrm{A}(-5\,; 6), trouver un couple de coordonnées possibles de \text{B}.
Sachant que \mathrm{A}(-5\,; 6), trouver un couple de coordonnées possibles de \text{B}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 70
Exercice inversé
Dans un repère orthonormé, on considère deux points \text{A} et \text{B}. Le taux d'accroissement entre les deux points est de \frac{5}{3}.
Sachant que \mathrm{B}(0,5 ; 6,5), trouver un couple de coordonnées possibles de \text{A}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah