Chapitre 10
TP Info
Approximation d'une fonction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soit f une fonction définie et dérivable sur un intervalle \text{I} de \R.
Soit a \in \mathrm{I}. Alors, pour tout x \in \mathrm{I} proche de a, on a
Il s'agit de l'approximation affine de f en a ou l'approximation polynomiale à l'ordre 1 de f en a.
Si f est deux fois dérivable, alors, pour tout x \in \mathrm{I} proche de a, on a :
Si f est trois fois dérivable, alors, pour tout x \in \mathrm{I} proche de a, on a :
Soit a \in \mathrm{I}. Alors, pour tout x \in \mathrm{I} proche de a, on a
f(x) \approx f(a)+(x-a) \times f^{\prime}(a).
Il s'agit de l'approximation affine de f en a ou l'approximation polynomiale à l'ordre 1 de f en a.
Si f est deux fois dérivable, alors, pour tout x \in \mathrm{I} proche de a, on a :
f(x) \approx f(a)+(x-a) \times f^{\prime}(a)+\frac{(x-a)^{2}}{2} \times f^{\prime \prime}(a) .
Il s'agit de l'approximation polynomiale à l'ordre 2 de f en a.Si f est trois fois dérivable, alors, pour tout x \in \mathrm{I} proche de a, on a :
f(x) \approx f(a)+(x-a) \times f^{\prime}(a)+\frac{(x-a)^{2}}{2} \times f^{\prime \prime}(a)+\frac{(x-a)^{3}}{6} \times f^{(3)}(a).
Il s'agit de l'approximation polynomiale à l'ordre 3 de f en a.
Notation
• f^{\prime \prime} est la dérivée seconde de la fonction f, c'est la dérivée de la fonction dérivée f^{\prime}.
• f^{(3)} est la dérivée d'ordre 3 de la fonction f , c'est la dérivée de la dérivée seconde f^{\prime \prime}.
• On note p_{i} l'approximation polynomiale à l'ordre i de f en a.
Par exemple, p_{1}(x)=f(a)+(x-a) \times f^{\prime}(a).
• f^{(3)} est la dérivée d'ordre 3 de la fonction f , c'est la dérivée de la dérivée seconde f^{\prime \prime}.
• On note p_{i} l'approximation polynomiale à l'ordre i de f en a.
Par exemple, p_{1}(x)=f(a)+(x-a) \times f^{\prime}(a).
Questions préliminaires
On considère la fonction f définie sur \R par f(x)=\sin (x).
1. Écrire l'approximation affine p_{1} de f en 0.
2. Écrire l'approximation polynomiale à l'ordre 2 p_{2} de f en 0, puis celle à l'ordre 3 p_{3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étudier la précision des approximations à l'ordre 1 et à l'ordre 3 de f en 0 à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode de résolution 1
Calculatrice
1. Régler la fenêtre d'affichage avec -1 \leqslant x \leqslant 1 et -1 \leqslant y \leqslant 1.
2. Représenter graphiquement la fonction f .
3. Représenter graphiquement la fonction p_{1}.
4. Pour quelles valeurs de x cette approximation semble-t-elle être la moins précise ?
5. Représenter graphiquement la fonction p_{3}.
6. Comparer les deux approximations polynomiales. Laquelle semble être la meilleure ?
2. Représenter graphiquement la fonction f .
3. Représenter graphiquement la fonction p_{1}.
5. Représenter graphiquement la fonction p_{3}.
6. Comparer les deux approximations polynomiales. Laquelle semble être la meilleure ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode de résolution 2
Tableur
On rappelle que p_{i} est l'approximation polynomiale à l'ordre i de f en 0. Reproduire la feuille de calcul ci-après pour x variant de -1 à 1 avec un pas de 0,1.
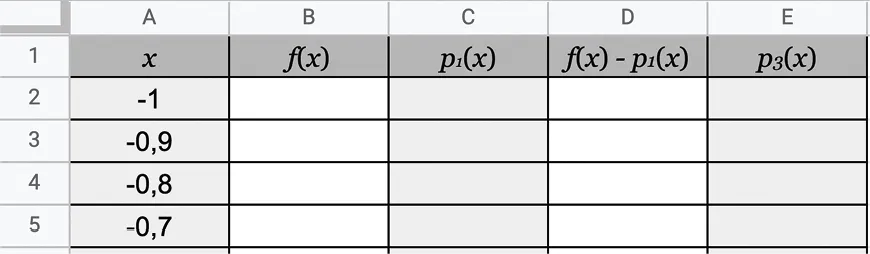1. Quelle formule doit-on saisir dans la cellule B2, puis étirer vers le bas, pour afficher les images de x par f dans la colonne B ?
2. Quelles formules doit-on saisir dans les cellules C2 et D2, puis étirer vers le bas pour compléter les colonnes C et D ?
3. À quoi correspondent les valeurs obtenues dans la colonne D ?
4. Compléter la colonne E pour obtenir les images de x par l'approximation polynomiale de f à l'ordre 3.
5. Quelles valeurs peut-on faire figurer dans la colonne F pour savoir si l'approximation polynomiale de f à l'ordre 3 est meilleure que l'approximation affine de f ?
2. Quelles formules doit-on saisir dans les cellules C2 et D2, puis étirer vers le bas pour compléter les colonnes C et D ?
4. Compléter la colonne E pour obtenir les images de x par l'approximation polynomiale de f à l'ordre 3.
5. Quelles valeurs peut-on faire figurer dans la colonne F pour savoir si l'approximation polynomiale de f à l'ordre 3 est meilleure que l'approximation affine de f ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut déterminer une approximation encore plus précise de f en utilisant l'approximation polynomiale de f en a à l'ordre 4 :
f(x) \approx f(a)+(x-a) \times f^{\prime}(a)+\frac{(x-a)^{2}}{2!} \times f^{\prime \prime}(a) +\frac{(x-a)^{3}}{3!} \times f^{(3)}(a)+\frac{(x-a)^{4}}{4!} \times f^{(4)}(a)
Indication
Pour tout entier naturel n non nul,
{n!=1 \times 2 \times 3 \times \ldots \times n} et n! se lit « n factorielle ».
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
