Justifier que l'équation de la tangente peut servir d'approximation pour le calcul des images d'une fonction.

1. On considère la fonction f définie sur l'intervalle [1\,; 5] par f(x)=x^{2}+6 x-3.
Dans un tableur, écrire dans la colonne A à partir de la cellule A2 les valeurs de x de 1 à 5 avec un pas de \text{0,1}.
2. Quelle est la formule à écrire dans la cellule B2 et à étirer vers le bas pour obtenir les images f(x) ?

3. On note \text{T} la tangente à la courbe représentative de f au point d'abscisse 3.
a. Montrer que l'équation réduite de \text{T} est \mathrm{T}: y=12 x-12.

b. On note alors g la fonction définie sur [1\,; 5] par l'expression de la tangente \text{T}, c'est-à-dire par g(x)=12 x-12.
Quelle est la formule à écrire dans la cellule C2 et à étirer vers le bas pour obtenir les images g(x) ?

c. Dans la colonne D, calculer la différence des colonnes B et C afin de comparer les images de x par f et par g.
Sur quel intervalle la différence entre les deux images est-elle inférieure à \text{0,5} ?

d. En quelle valeur cette différence est-elle nulle ? Pouvait-on prévoir ce résultat ?

4. Cas général : Écrire la formule donnant l'équation réduite de la tangente à la courbe représentative d'une fonction f au point d'abscisse a. Que se passe-t-il lorsque a se rapproche de x ?

Il est donc possible d'approcher la valeur des images de la fonction à l'aide des tangentes à sa courbe représentative. Quelle est la condition à respecter pour obtenir la meilleure approximation possible ?

Démontrer la formule de dérivation d'un produit de deux fonctions.

1. Écrire les taux de variation des fonctions u et v entre x et x + h.

2. On pose, pour tout x \in \mathrm{I}, f(x)=u(x) \times v(x).
On admet que la fonction f est une fonction définie et dérivable sur \text{I} en tant que produit de fonctions dérivables. Écrire le taux de variation de f entre x et x + h.

3. Vérifier que ce taux de variation est égal à \frac{u(x+h)-u(x)}{h} \times v(x+h)+u(x) \times \frac{v(x+h)-v(x)}{h}.

4. En utilisant les formules de la question 1 et en faisant tendre h vers 0, obtenir la formule de dérivation d'un produit u \times v de deux fonctions.

Si u et v sont deux fonctions dérivables sur un intervalle \text{I}, quelle est la dérivée de \boldsymbol{u} \times \boldsymbol{v} ?

Découvrir de nouvelles formules de dérivation

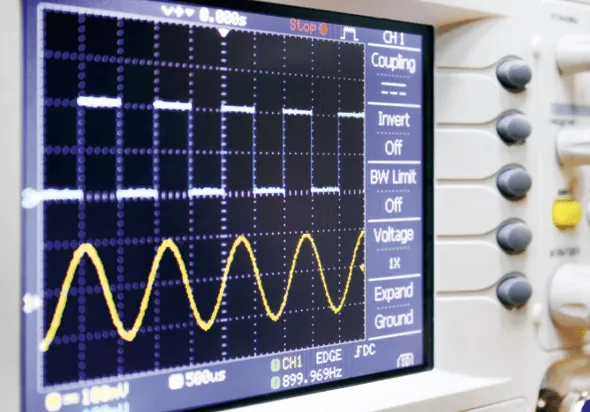
1. Quelle est la position du point au bout de \text{4,5} secondes ?

2. Déterminer un temps t_0 pour lequel le point se situe sur l'axe des abscisses.

a. Analyser la fonction obtenue. Qu'est-il advenu de la fonction trigonométrique ? À quoi correspond le coefficient apparu hors de la fonction ?

b. Quelle est la vitesse du point au bout de 4,5 secondes ?

4. On veut déterminer l'accélération du point au bout de \text{4,5} secondes. Pour obtenir l'accélération a(t) du point à l'instant t, on dérive la fonction vitesse v.
Pour cela, on utilise un logiciel de calcul formel affichant le résultat suivant.
a. Analyser la fonction obtenue. Qu'est-il advenu de la fonction trigonométrique ? À quoi correspond le coefficient apparu hors de la fonction ?

b. Quelle est l'accélération du point au bout de \text{4,5} secondes ?

5. Soient f une fonction dérivable sur \R, et a et b deux réels.
On admet que la dérivée de la fonction t \mapsto f(a t+b) est donnée par la fonction définie pour tout réel t par t \mapsto a \times f^{\prime}(a t+b).
a. Déterminer alors les dérivées des fonctions t \mapsto \cos (a t+b) et t \mapsto \sin (a t+b).

b. Les résultats confirment-ils les observations décrites aux questions 3 a et 3 a ?

Soient a et b deux réels. Quelles sont les formules de dérivation des fonctions trigonométriques {t} \mapsto \cos ({a} {t}+{b}) et t \mapsto \sin (a t+b) ?