Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Automatismes
Ch. 1
Statistiques à une variable
Ch. 2
Fluctuations d'une fréquence et probabilités
Ch. 3
Résolution d'un problème du premier degré
Ch. 4
Représentation et variations d'une fonction
Ch. 5
Fonctions affines, fonction carré
Ch. 6
Calculs commerciaux et financiers
Ch. 7
Géométrie
Fiches méthodes
Chapitre 5
Activité B
#TIC
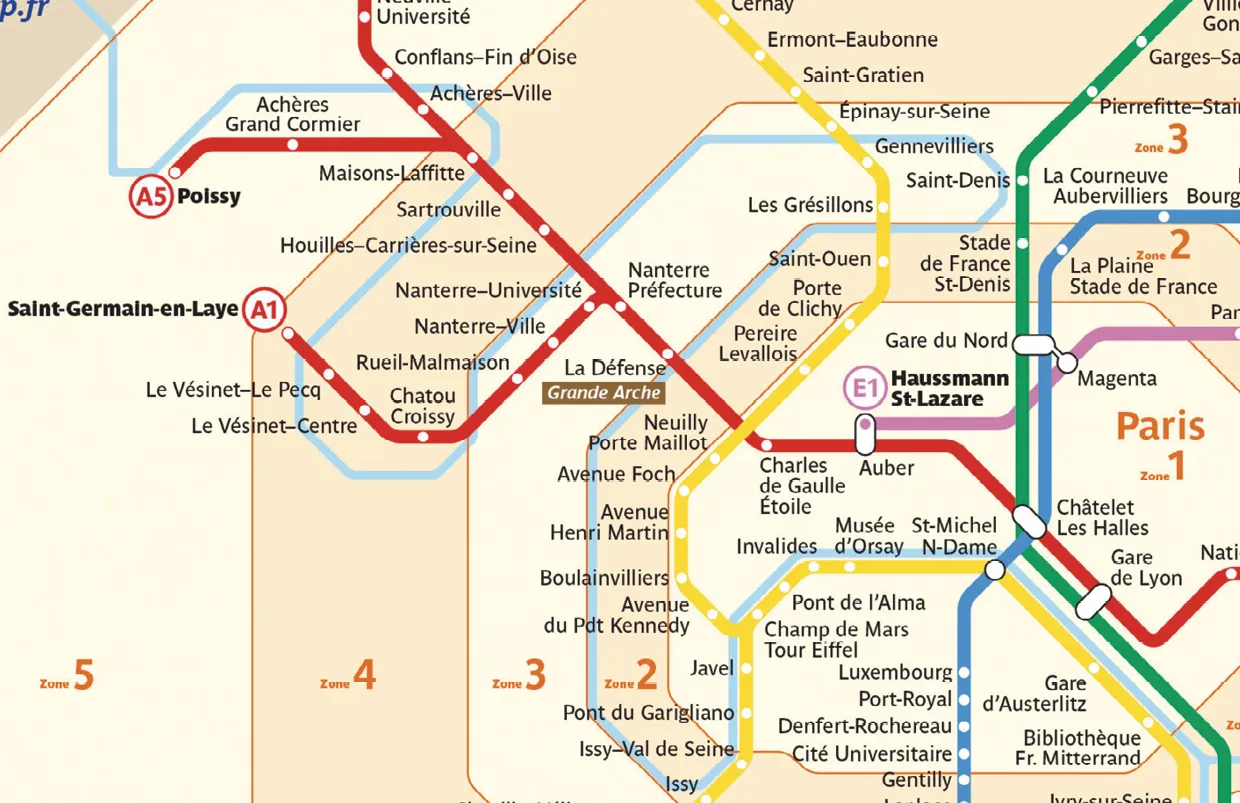
Réseau des transports en Île-de-France
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Résoudre graphiquement un système de deux équations du premier degré à deux inconnues.
Résoudre graphiquement un système de deux équations du premier degré à deux inconnues.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Andréas est en seconde professionnelle dans un lycée parisien. Chaque semaine, il utilise les transports en commun pour rentrer soit chez son père, qui habite vers Haussmann―Saint-Lazare, soit chez sa mère qui habite le quartier de La Défense.
Une partie du plan du réseau régional des transports en Île‑de‑France est donnée ci-contre.
Une partie du plan du réseau régional des transports en Île‑de‑France est donnée ci-contre.
- Lors de la première semaine, Andréas est rentré trois jours chez son père (soit six billets) et deux jours chez sa mère (soit quatre billets) et il a payé 22,60 €.
- Lors de la deuxième semaine, Andréas est rentré un jour chez son père (soit deux billets) et quatre jours chez sa mère (soit huit billets) et il a payé 24,20 €.
Problématique
Quel montant va-t-il devoir payer ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
1
S'APPROPRIERDéterminer les zones de transport dans lesquelles habitent le père et la mère d'Andréas, à l'aide du plan régional des transports en Île‑de‑France.
2
ANALYSER/RAISONNERProposer une méthode de résolution permettant de répondre à la problématique.
On modélise cette situation par le système de deux équations à deux inconnues ci-dessous.
\left\{\begin{array}{l}
6 x+4 y=22,60 \\
2 x+8 y=24,20
\end{array}\right.
3
S'APPROPRIERIndiquer ce que représentent les deux inconnues x et y.
4
RÉALISERTracer les deux droites correspondant à chacune des équations, à l'aide des outils numériques. Ici, la .
Cliquez pour accéder à un module GeoGebra
GeoGebra
5
RÉALISERDéterminer les coordonnées du point d'intersection de ces deux droites.
6
VALIDERVérifier que le couple de coordonnées de ce point d'intersection est solution de chacune des deux équations du système.
Coup de pouce
Pour vérifier qu'un couple de valeurs est solution d'une équation, on remplace x et y par leur valeur dans l'équation.
7
S'APPROPRIEREn déduire le prix d'un billet pour chacune des zones de transport 1 et 3.
8
RÉALISERCalculer le montant que va devoir payer Andréas la semaine prochaine.
9
COMMUNIQUERRédiger un message à Andréas afin de répondre de façon détaillée à la problématique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je fais le bilanQu'est-ce que j'ai appris ?
Fais le bilan de ce que tu as appris lors de cette activité à l'aide d'une carte mentale.
Cliquez pour accéder à un espace de dessin
Cette fonctionnalité est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah