Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Automatismes
Ch. 1
Statistiques à une variable
Ch. 2
Fluctuations d'une fréquence et probabilités
Ch. 3
Résolution d'un problème du premier degré
Ch. 4
Représentation et variations d'une fonction
Ch. 5
Fonctions affines, fonction carré
Ch. 6
Calculs commerciaux et financiers
Ch. 7
Géométrie
Fiches méthodes
Chapitre 5
L'essentiel
Fonctions affines, fonction carré et systèmes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Fonction affine f(x)=ax+b
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
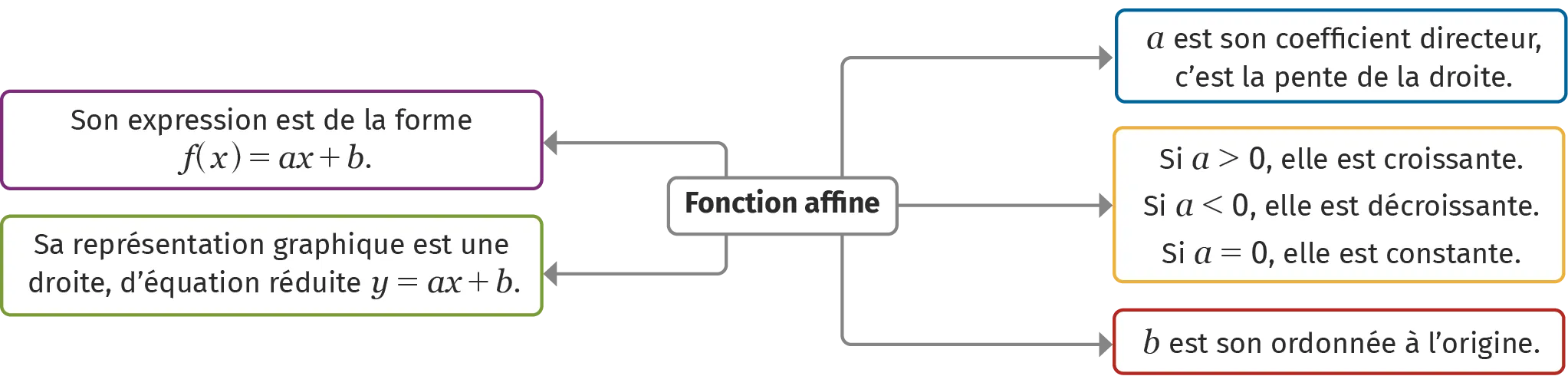
Une fonction affine f est une fonction définie sur \mathbb{R} dont l'expression est de la forme \bold{f(x)=a x+b} avec a et b réels.
La représentation graphique d'une fonction affine est une droite d'équation réduite y=ax+b.
Le sens de variation d'une fonction affine d'expression f(x)=ax+b dépend du signe de a :
La représentation graphique d'une fonction affine est une droite d'équation réduite y=ax+b.
- a est le cœfficient directeur de la droite ou taux d'accroissement de la fonction.
- b est l'ordonnée à l'origine de la droite.
- si a=0, f(x)=b, la fonction est alors constante ;
- si b=0, f(x)=ax, la fonction est alors linéaire.
Remarque
Deux droites d'équations données sont parallèles si elles ont le même cœfficient directeur.
- si a>0, la fonction est croissante ;
- si a\lt 0, la fonction est décroissante ;
- si a=0, la fonction est constante.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On considère deux fonctions affines f et g définies sur \mathbb{R} par f(x)=2x-4 et g(x)=-3x+2 dont les droites représentatives
sont données ici.
Dans un repère orthonormé, le cœfficient directeur correspond à la pente de la droite.
Dans un repère orthonormé, le cœfficient directeur correspond à la pente de la droite.
- La fonction f est croissante sur \mathbb{R} car a=\color{green}2\color{black}>0.
- La fonction g est décroissante sur \mathbb{R} car a=\color{red}-3\color{black}\lt 0.
Le zoom est accessible dans la version Premium.
On peut également déterminer algébriquement l'expression f(x)=ax+b d'une fonction affine à partir de la donnée de deux nombres x_1 et x_2 et de leurs images f(x_1) et f(x_2).
- Pour déterminer a, on calcule le taux d'accroissement a=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}.
- Pour déterminer b, on résout l'équation f\left(x_1\right)=a x_1+b.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice résolu
1. Déterminer algébriquement l'expression de la fonction affine f à partir des deux points \mathrm{E}(2;3) et
\mathrm{F}(4;9) qui appartiennent à sa droite représentative.
1re étape : Pour déterminer le cœfficient directeur a, on calcule le taux d'accroissement :
a=\frac{f\left(x_\mathrm{F}\right)-f\left(x_\mathrm{E}\right)}{x_\mathrm{F}-x_\mathrm{E}}=\frac{9-3}{4-2}=\frac{6}{2}=3
On obtient donc l'expression f(x)=3x+b.
2e étape : Pour déterminer l'ordonnée à l'origine b, on choisit le point \mathrm{E} ou le point \mathrm{F} et on intègre ses coordonnées dans l'expression.
On choisit par exemple le point \mathrm{F}.
On a f(x)=3x+b, on remplace x par 4 et f(x) par 9.
On obtient 9=3\times 4+b, on résout alors l'équation.
\iff 9=12+b
\iff 9-12=12+b-12
\iff b=-3
L'expression de la fonction affine f est donc f(x)=3 x-3.
1re étape : Pour déterminer le cœfficient directeur a, on calcule le taux d'accroissement :
a=\frac{f\left(x_\mathrm{F}\right)-f\left(x_\mathrm{E}\right)}{x_\mathrm{F}-x_\mathrm{E}}=\frac{9-3}{4-2}=\frac{6}{2}=3
On obtient donc l'expression f(x)=3x+b.
2e étape : Pour déterminer l'ordonnée à l'origine b, on choisit le point \mathrm{E} ou le point \mathrm{F} et on intègre ses coordonnées dans l'expression.
On choisit par exemple le point \mathrm{F}.
On a f(x)=3x+b, on remplace x par 4 et f(x) par 9.
On obtient 9=3\times 4+b, on résout alors l'équation.
\iff 9=12+b
\iff 9-12=12+b-12
\iff b=-3
L'expression de la fonction affine f est donc f(x)=3 x-3.
2. Vérifier graphiquement l'expression obtenue.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Système de deux équations à deux inconnues
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Un système de deux équations du premier degré à deux inconnues est composé de deux équations dans lesquelles se trouvent deux inconnues, que l'on note généralement par les lettres x et y.
- Résoudre un système de deux équations à deux inconnues revient à déterminer le couple solution qui vérifie chacune des deux équations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Soit le système de deux équations à deux inconnues suivant.
\left\{\begin{array}{c}
\color{red}2x+3 y=1\\
\color{green}-5 x+4 y=-14
\end{array}\right.
- On représente graphiquement les droites correspondant à chacune des deux équations du système
- On relève sur le graphique le couple de coordonnées du point d'intersection \mathrm{A} de ces deux droites (2;-1), c'est-à-dire qui a pour abscisse x=2 et pour ordonnée y=-1.
Le zoom est accessible dans la version Premium.
- On vérifie que ce couple de valeurs est bien solution du système en remplaçant x par 2 et y par -1 dans chacune des deux équations.
- Le couple (2;-1) est donc solution du système.
\left\{\begin{aligned}
2 \times \color{blue}2\color{black}+3 \times\color{purple}(-1)\color{black}&=4-3=1 \\
-5 \times \color{blue}2\color{black}+4 \times\color{purple}(-1)\color{black}&=-10-4=-14
\end{aligned}\right.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Fonction carré f(x)=x^2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
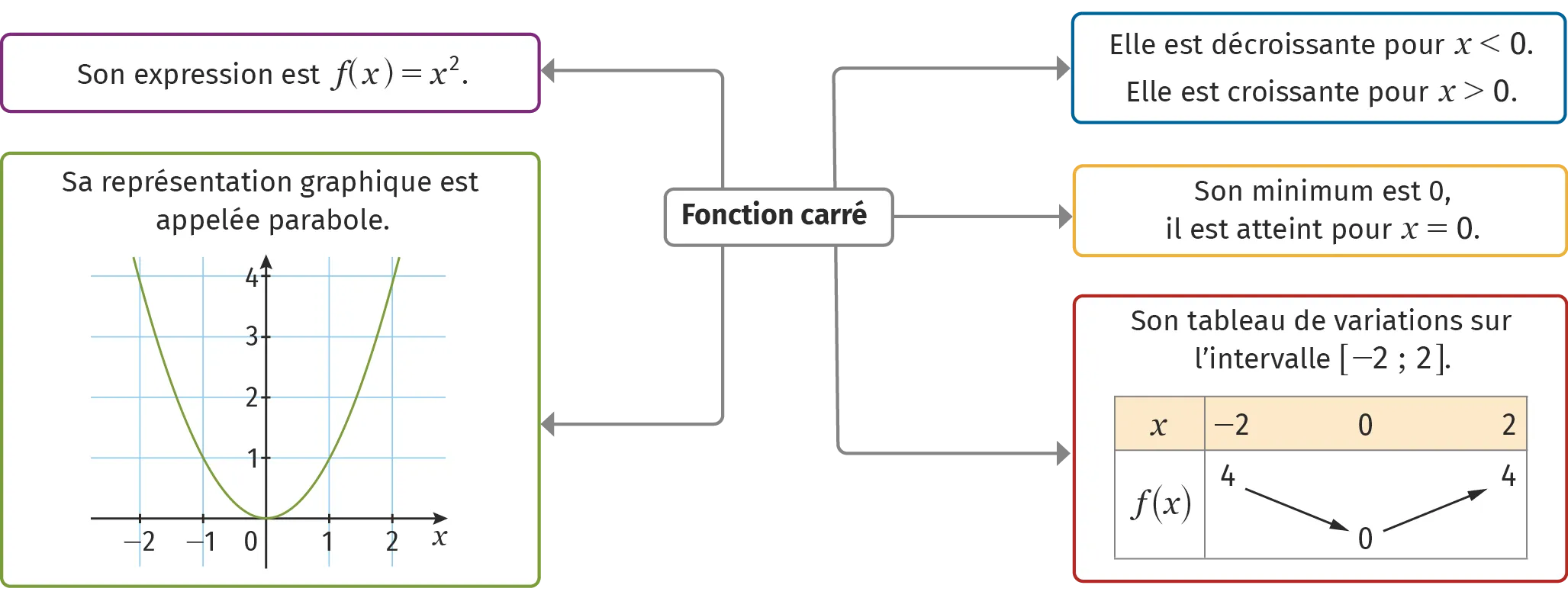
La fonction f définie sur \mathbb{R} par f(x)=x^2 est appelée la fonction carré. La courbe représentative de cette fonction est appelée parabole.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Opérations sur les fonctions f+k et kf
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Addition d'une constante à une fonction : lorsque l'on ajoute un nombre k à une fonction f, on obtient une fonction f+k qui a le même sens de variation que f.
- Multiplication d'une fonction par une constante : lorsque l'on multiplie une fonction f par un nombre k, on obtient une fonction kf qui a le même sens de variation que f si k>0 et qui a le sens de variation contraire si k\lt 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On considère la courbe représentative de la fonction f définie sur \mathbb{R} par f(x)=x^2.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Résolution d'une équation du type f(x)=c ou d'une inéquation
du type f(x)\lt c
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Résoudre une équation du type f(x)=c, où c est un réel donné, revient à trouver les solutions, si elles existent, qui correspondent aux abscisses des points d'intersection de la courbe représentative de la fonction f et la droite d'équation y=c.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Résoudre une inéquation du type f(x)\lt c, où c est un réel donné, revient à trouver les solutions, si elles existent, qui correspondent à l'ensemble des abscisses pour lesquelles la courbe représentative de la fonction f est située en dessous de la droite d'équation y=c.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On considère la droite représentative de la fonction f définie sur \mathbb{R} par \color{green}{f(x)=2x+4} et la droite d'équation y=10 ci-dessous.
La solution de l'équation \color{green}{f(x)}=\color{red}{10} est l'abscisse du point d'intersection \mathrm{A} de la droite représentative de la fonction f et de la droite d'équation y=10, soit x=3.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On considère la courbe représentative de la fonction f définie sur \mathbb{R} par f(x)=0,8x^2et la droite d'équation y=5 ci-dessous.
Les solutions de l'équation \color{green}f(x)\color{black}\lt \color{red}5 sont l'ensemble des abscisses pour lesquelles la courbe représentative de la fonction f est située en dessous de la droite d'équation y=5, soit l'intervalle ]-2,5 ; 2,5[.
Le zoom est accessible dans la version Premium.
Les solutions de l'équation \color{green}f(x)\color{black}\lt \color{red}5 sont l'ensemble des abscisses pour lesquelles la courbe représentative de la fonction f est située en dessous de la droite d'équation y=5, soit l'intervalle ]-2,5 ; 2,5[.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah