Enseignement mathématique 1re
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Exercices rituels et automatismes
Exercices rituels
Automatismes
Partie 1 - Information chiffrée
Ch. 1
Analyse de l'information chiffrée
Partie 2 - Probabilités
Ch. 2
De la statistique aux probabilités
Partie 3 - Phénomènes d’évolution
Ch. 3
Croissance linéaire
Ch. 4
Croissance exponentielle
Partie 4 - Dérivation
Ch. 5
Variations instantanées
Ch. 6
Variations globales
GeoGebra
Partie 2
Histoire des mathématiques
Probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une histoire des probabilités
C'est à Gerolamo Cardano (1501-1576) que l'on doit la toute première tentative de
mathématiser les probabilités, dans son livre Liber de ludo alea (1564). Cependant,
un des points de départ d'une réflexion scientifique sur les probabilités est le
célèbre problème des partis, énoncé pour la première fois en 1494 par Luca Pacioli
(1445-1517) dans son encyclopédie mathématique, la Summa de Arithmetica, Geometria,
Proportioni et Proportionalita (voir ci-après).
150 ans plus tard, Blaise Pascal (1623-1662) et Pierre de Fermat (1607-1665) échangent sur ce même problème, qui porte alors le nom du problème du chevalier de Méré, afin de lui apporter une solution généralisable. S'inspirant de ces échanges, Christian Huygens (1629-1695) publie en 1657 son Tractatus de Ratiociniis in Alea Ludo qui constitue le premier traité mathématique consacré aux probabilités et ouvre la voie à cette nouvelle branche des mathématiques.
150 ans plus tard, Blaise Pascal (1623-1662) et Pierre de Fermat (1607-1665) échangent sur ce même problème, qui porte alors le nom du problème du chevalier de Méré, afin de lui apporter une solution généralisable. S'inspirant de ces échanges, Christian Huygens (1629-1695) publie en 1657 son Tractatus de Ratiociniis in Alea Ludo qui constitue le premier traité mathématique consacré aux probabilités et ouvre la voie à cette nouvelle branche des mathématiques.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le problème des partis
On peut résumer le problème dont il est question dans les échanges épistolaires
entre Pascal et Fermat de la façon suivante : deux joueurs (appelés
partis) misent chacun 32 pistoles et participent à un jeu qui se gagne au
meilleur des cinq manches. Le gagnant remporte la somme des deux mises
soit 64 pistoles. Si le jeu est interrompu avant de pouvoir arriver à sa fin (par exemple sur le score de deux manches à une), comment les joueurs
doivent‑ils se répartir les gains pour l'équité ?
Ni Pascal ni Fermat ne parlent encore de probabilités mais chacun calculent pourtant ce qui s'apparente à des espérances de gains. Fermat apporte une solution qui se base sur le dénombrement alors que Pascal choisit une solution élégante qui s'appuie sur son triangle arithmétique. Les solutions présentées dans ces échanges épistolaires sont généralisables à d'autres situations.
Ni Pascal ni Fermat ne parlent encore de probabilités mais chacun calculent pourtant ce qui s'apparente à des espérances de gains. Fermat apporte une solution qui se base sur le dénombrement alors que Pascal choisit une solution élégante qui s'appuie sur son triangle arithmétique. Les solutions présentées dans ces échanges épistolaires sont généralisables à d'autres situations.





Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
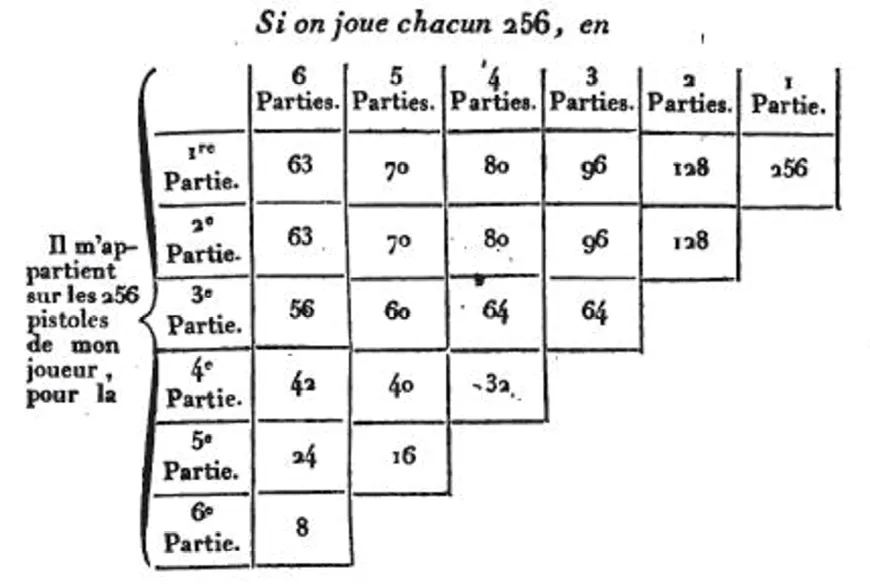
Solution proposée par Pascal
Pascal explique un premier principe : si les deux partis (ayant la même chance de gagner) ont deux victoires chacun,
lors de la partie suivante, l'un emportera la mise et l'autre rien. L'espérance du gain est donc \frac{1}{2} \times 64+\frac{1}{2} \times 0=32. Puis, il procède à reculons comme on l'illustre avec les arbres suivants.



L'espérance de gains lors de cette étape 2 est donc {\frac{1}{2} \times 64+\frac{1}{2} \times 32=48}. Il remonte alors toutes les étapes pour obtenir les espérances de gains à tous les instants où la partie peut s'interrompre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Probabilités conditionnelles et indépendance
Dans The Doctrine of Chances publié à Londres en 1718, Abraham de Moivre
(1667-1754) est le premier mathématicien à aborder la notion d'indépendance
d'événements. C'est à une œuvre de Thomas Bayes (1702-1761), publiée à titre
posthume en 1763 par son ami mathématicien Richard Price (1723-1791), que
l'on doit la première théorie sur les probabilités conditionnelles : An Essay
towards Solving a Problem in the Doctrine of Chances.



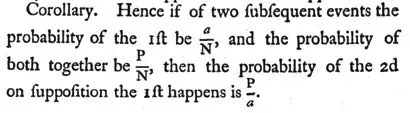
Le corollaire ci-dessus fait partie de la proposition 3 du livre et correspond à la définition que l'on donne aujourd'hui de la probabilité d'un événement \mathrm{B} conditionné par un événement {\mathrm{A}: \mathrm{P}_\mathrm{{A}}(\mathrm{B})=\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}} lorsque \mathrm{P}(\mathrm{A}) \neq 0
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
