Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Automatismes
Ch. 1
Statistiques à une variable
Ch. 2
Fluctuations d'une fréquence et probabilités
Ch. 3
Résolution d'un problème du premier degré
Ch. 4
Représentation et variations d'une fonction
Ch. 5
Fonctions affines, fonction carré
Ch. 6
Calculs commerciaux et financiers
Ch. 7
Géométrie
Fiches méthodes
Chapitre 1
L'essentiel
Statistique à une variable
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Un peu de vocabulaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- La population correspond à l'ensemble des personnes, ou des objets, sur lesquels porte l'étude statistique.
- Le caractère, ou la variable, correspond à la propriété sur laquelle porte l'étude statistique.
- Un caractère est qualitatif s'il est non mesurable. (Exemple : moyen de transport.)
- Un caractère est quantitatif discret s'il est mesurable et s'il ne peut prendre qu'un nombre fini de valeurs. (Exemple : nombre de frères et sœurs.)
- Un caractère est quantitatif continu s'il est mesurable et s'il peut prendre toutes les valeurs d'un intervalle donné. Cet intervalle s'appelle une classe de valeurs. (Exemple : temps de trajet.)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On étudie les résultats des élèves d'une classe de terminale au baccalauréat professionnel.
La population étudiée correspond aux élèves de cette classe de terminale.
Le caractère étudié correspond au résultat obtenu au bac. Ce caractère est qualitatif car il ne se représente pas par un nombre.
Pour calculer la fréquence des élèves qui ont obtenu le bac, on divise l'effectif des élèves qui ont obtenu le bac par l'effectif total : {f=\frac{\color{green}21}{\color{blue}24}=0,875} soit 87,5 %. Dans cette classe de terminale, 87,5 % des élèves ont obtenu le baccalauréat professionnel.
Résultat | Refusé | Admis | Mention Assez Bien | Mention Bien | Mention Très Bien | Total |
|---|---|---|---|---|---|---|
Nombre d'élèves | 3 | 6 | 8 | 6 | 1 | 24 |
Le caractère étudié correspond au résultat obtenu au bac. Ce caractère est qualitatif car il ne se représente pas par un nombre.
Pour calculer la fréquence des élèves qui ont obtenu le bac, on divise l'effectif des élèves qui ont obtenu le bac par l'effectif total : {f=\frac{\color{green}21}{\color{blue}24}=0,875} soit 87,5 %. Dans cette classe de terminale, 87,5 % des élèves ont obtenu le baccalauréat professionnel.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Représentations graphiques d'une série statistique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Il existe différents diagrammes pour représenter une série statistique. Le diagramme le plus adapté dépend principalement de la nature du caractère.
Le diagramme en secteurs convient à toute nature de caractère. Les mesures des angles sont proportionnelles aux effectifs ou aux fréquences.
Le diagramme en bâtons convient à un caractère qualitatif ou quantitatif discret. Les hauteurs des bâtons sont proportionnelles aux effectifs ou aux fréquences.
Le diagramme en colonnes convient à un caractère quantitatif continu dont les valeurs ont été regroupées par classes.
Le diagramme à lignes brisées convient pour représenter un phénomène chronologique quantitatif. Le temps est alors représenté en abscisse et les valeurs du caractère sont représentées en ordonnée.
Exemple
Le diagramme en secteurs convient à toute nature de caractère. Les mesures des angles sont proportionnelles aux effectifs ou aux fréquences.
Le zoom est accessible dans la version Premium.
Exemple
Le diagramme en bâtons convient à un caractère qualitatif ou quantitatif discret. Les hauteurs des bâtons sont proportionnelles aux effectifs ou aux fréquences.
Le zoom est accessible dans la version Premium.
Exemple
Le zoom est accessible dans la version Premium.
Exemple
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Les indicateurs statistiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Il existe deux types d'indicateurs statistiques qui peuvent se calculer avec les fonctions statistiques d'une calculatrice ou d'un tableur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
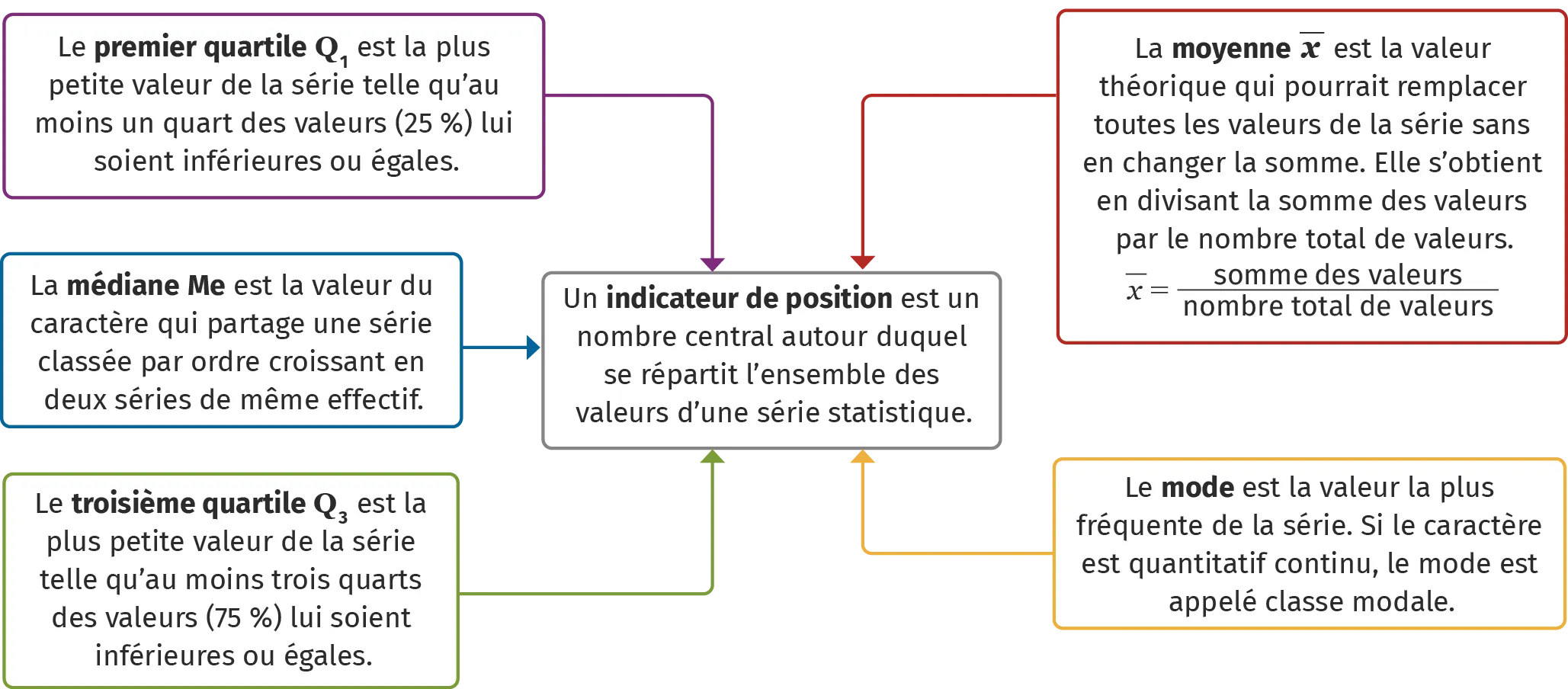
ALes indicateurs de position
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On s'intéresse aux températures mensuelles moyennes à Paris en 2020.
Mois | J | F | M | A | M | J | J | A | S | O | N | D |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
T (°C) | 7,1 | 9,3 | 9,4 | 15,7 | 16,8 | 19,2 | 21,1 | 22,9 | 19,3 | 12,9 | 10,2 | 7,1 |
Indicateur de position | Moyenne | Mode | 1er quartile | Médiane | 3e quartile |
|---|---|---|---|---|---|
Température (en °C) | 14,25 | 7,1 | 9,3 | 14,3 | 19,2 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BLes indicateurs de dispersion
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On s'intéresse à la série statistique représentant les températures mensuelles moyennes à Paris en 2020.
Indicateur de dispersion | Étendue | Écart type | Écart interquartile |
|---|---|---|---|
Température (en °C) | e=\operatorname{Max}-\operatorname{Min}=22,9-7,1=15,8 | \sigma=5,4 | \mathrm{Q}_3-\mathrm{Q}_1=19,2-9,3=9,9 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Le diagramme en boîte à moustaches
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Un diagramme en boîte à moustaches permet de visualiser graphiquement la dispersion d'une série statistique autour de la médiane. On peut lire sur ce diagramme le minimum, le premier quartile, la médiane, le troisième quartile et le maximum d'une série statistique.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On représente les notes obtenues par les élèves d'une classe lors d'un contrôle de mathématiques par le diagramme en boîte à moustaches ci-dessous.
1. On relève les différents indicateurs de position à partir du diagramme en boîte à moustaches.
2. On calcule les différents indicateurs de dispersion à partir du tableau précédent.
Le zoom est accessible dans la version Premium.
1. On relève les différents indicateurs de position à partir du diagramme en boîte à moustaches.
Indicateur de position | Minimum | 1er quartile | Médiane | 3e quartile | Maximum |
|---|---|---|---|---|---|
Note | 2 | 5 | 10 | 12 | 17 |
2. On calcule les différents indicateurs de dispersion à partir du tableau précédent.
Indicateur de dispersion | Étendue | Écart interquartile |
|---|---|---|
Note | e=\operatorname{Max}-\operatorname{Min}=17-2=15 | Q_3-Q_1=12-5=7 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice résolu
Un enseignant réalise un sondage auprès des élèves d'une classe pour connaître le temps qu'ils passent dans les transports chaque jour pour venir au lycée. Les résultats sont regroupés par classes dans le tableau ci-dessous.
Remarques :
Temps (en min) | [0 ; 10[ | [10 ; 20[ | [20; 30[ | [30; 40[ | [40 ; 50[ | [50 ; 60[ |
|---|---|---|---|---|---|---|
Nombre d'élèves | 3 | 11 | 8 | 5 | 2 | 1 |
Remarques :
- Lorsque le crochet est tourné vers l'extérieur (l'intervalle est ouvert), la valeur n'est pas comprise dans l'intervalle, on dit qu'elle est exclue.
- Lorsque le crochet est tourné vers l'intérieur (l'intervalle est fermé), la valeur est comprise dans l'intervalle, on dit qu'elle est incluse.
1. Indiquer le diagramme le plus pertinent pour représenter cette série statistique, en justifiant.
Le diagramme en colonnes est le plus pertinent pour représenter cette série car le caractère étudié est quantitatif continu et les valeurs sont 10 regroupées par classes.
Le diagramme en colonnes est le plus pertinent pour représenter cette série car le caractère étudié est quantitatif continu et les valeurs sont 10 regroupées par classes.
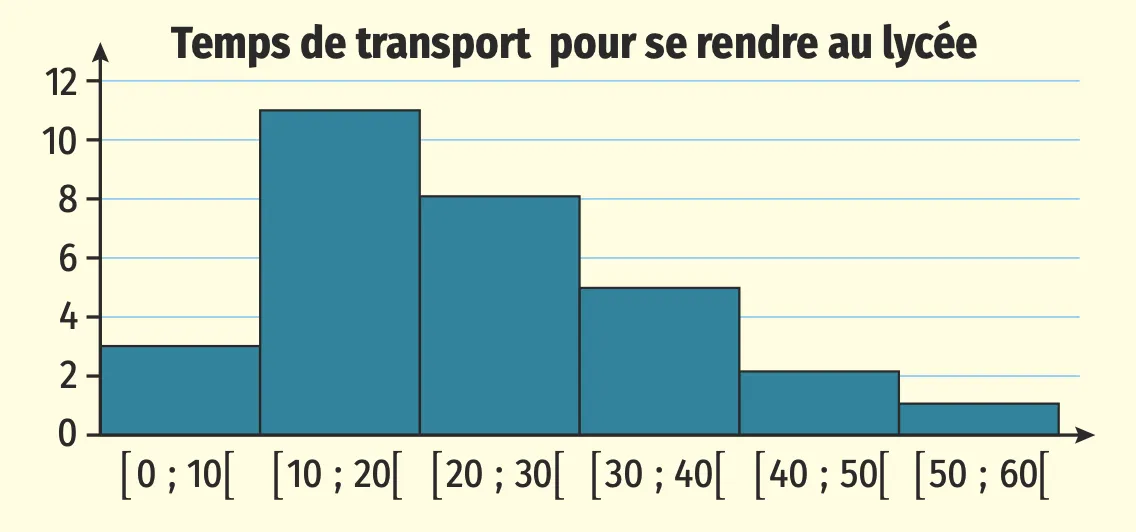
2. Construire le diagramme choisi, à l'aide des outils numériques.
Le zoom est accessible dans la version Premium.
3. Justifier l'intérêt de regrouper les valeurs par classes.
L'intérêt de regrouper les valeurs par classes est de :
L'intérêt de regrouper les valeurs par classes est de :
- constituer des classes ayant un effectif suffisant pour permettre une meilleure interprétation et ainsi rendre l'exploitation statistique plus pertinente ;
- construire des diagrammes statistiques qui auront davantage de sens.
4. Interpréter ce diagramme en colonnes.
Dans ce diagramme en colonnes, on peut voir que tous les élèves de la classe mettent moins d'une heure pour se rendre au lycée et que la majorité des élèves mettent entre 10 et 30 minutes.
Dans ce diagramme en colonnes, on peut voir que tous les élèves de la classe mettent moins d'une heure pour se rendre au lycée et que la majorité des élèves mettent entre 10 et 30 minutes.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah