Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 11
TP / TICE
L'affaire Castaneda contre Partida
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
En 1976, Rodrigo Partida est condamné à huit ans de prison pour un cambriolage dans un comté du sud du Texas. Il conteste ce jugement en affirmant que la méthode de désignation des jurés est discriminatoire : sur les 870 personnes convoquées pour être jurés lors des 11 dernières années, seulement 339 étaient d'origine mexicaine alors qu'ils représentent 79,1 % des habitants de ce comté.
Question préliminaire :
Comparer la fréquence de jurés d'origine mexicaine avec la proportion d'Américains d'origine mexicaine qui vivent dans ce comté.
Question préliminaire :
Comparer la fréquence de jurés d'origine mexicaine avec la proportion d'Américains d'origine mexicaine qui vivent dans ce comté.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Réaliser une simulation avec l'une des deux méthodes proposées afin de déterminer si la contestation de Roberto Partida est recevable.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1 Tableur
1. a. Pour simuler la désignation d'un juré, entrer
dans la cellule A1 d'un tableur la formule :
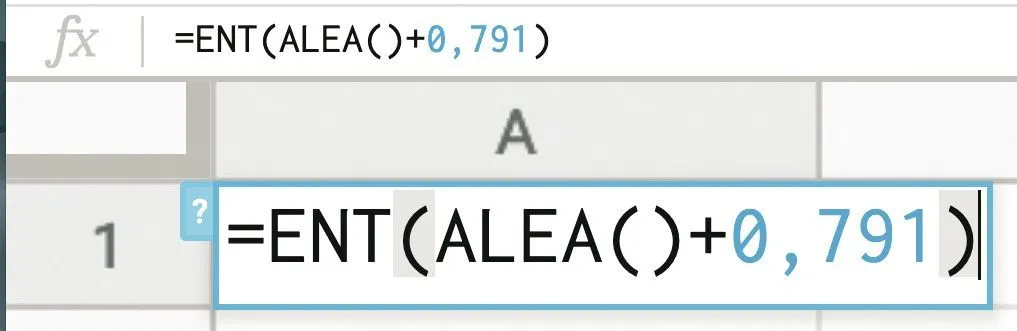
b. Quelle est la probabilité que le nombre qui s'affiche soit 1 \: ?
c. Compléter la phrase suivante :
« signifie que le juré désigné est d'origine mexicaine et signifie qu'il ne l'est pas. »
d. Étirer cette formule jusqu'en A870 pour simuler le tirage des 870 jurés.
2. En A872, calculer la fréquence de jurés d'origine mexicaine. Étirer les formules de la colonne A jusqu'en CV pour simuler 100 fois le tirage d'un jury de 870 personnes.
Le zoom est accessible dans la version Premium.
b. Quelle est la probabilité que le nombre qui s'affiche soit 1 \: ?
c. Compléter la phrase suivante :
«
d. Étirer cette formule jusqu'en A870 pour simuler le tirage des 870 jurés.
2. En A872, calculer la fréquence de jurés d'origine mexicaine. Étirer les formules de la colonne A jusqu'en CV pour simuler 100 fois le tirage d'un jury de 870 personnes.
3. Représenter les fréquences obtenues sous la forme
d'un nuage de points.
4. Effectuer plusieurs simulations en appuyant sur F9 et estimer un intervalle dans lequel devrait se trouver la fréquence de jurés d'origine mexicaine dans ce comté.
5. La proportion de jurés d'origine mexicaine dans l'énoncé semble-t-elle cohérente avec les simulations obtenues ?
6. La contestation de Roberto Partida semble-t-elle recevable ?
4. Effectuer plusieurs simulations en appuyant sur F9 et estimer un intervalle dans lequel devrait se trouver la fréquence de jurés d'origine mexicaine dans ce comté.
5. La proportion de jurés d'origine mexicaine dans l'énoncé semble-t-elle cohérente avec les simulations obtenues ?
6. La contestation de Roberto Partida semble-t-elle recevable ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
>Méthode 2 Python
1. a. Quelle est la probabilité que l'instruction int(random() + 0,791) renvoie 1 \: ?
b. Compléter la phrase suivante :
« signifie que le juré désigné est d'origine mexicaine et signifie qu'il ne l'est pas. »
c. Compléter ce programme pour qu'il affiche les fréquences de jurés d'origine mexicaine pour chaque jury tiré au sort.
2. Effectuer plusieurs simulations et estimer un intervalle dans lequel devrait se trouver la fréquence de jurés d'origine mexicaine dans ce comté.
3. La proportion de jurés d'origine mexicaine trouvée précédemment semble-t-elle cohérente avec les simulations obtenues ?
4. La contestation de Roberto Partida semble-t-elle recevable ?
b. Compléter la phrase suivante :
«
c. Compléter ce programme pour qu'il affiche les fréquences de jurés d'origine mexicaine pour chaque jury tiré au sort.
2. Effectuer plusieurs simulations et estimer un intervalle dans lequel devrait se trouver la fréquence de jurés d'origine mexicaine dans ce comté.
3. La proportion de jurés d'origine mexicaine trouvée précédemment semble-t-elle cohérente avec les simulations obtenues ?
4. La contestation de Roberto Partida semble-t-elle recevable ?
from math import *
from random import random
import matplotlib.pyplot as plt
N = 1000
for k in range(...):
Compteur = 0
for i in range(...):
x = int(random() + 0.791)
if ...:
Compteur = Compteur + 1
f = ...
plt.plot(k, f, 'ob')
plt.plot([0,N-1], [0.791-1/sqrt(869),0.791-1/sqrt(869)], "r")
plt.plot([0,N-1], [0.791+1/sqrt(869),0.791+1/sqrt(869)], "r")
plt.show()
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah