L'abbé Nollet, au XVIII^e siècle, met au point un appareil capable de mettre en évidence la charge électrique d'un objet. Pour ce faire, on approche l'objet chargé du sommet de l'électroscope, sans le toucher. La partie conductrice de celui-ci s'électrise par influence et les deux feuilles métalliques s'écartent l'une de l'autre.

Schématiser la répartition des charges dans la partie conductrice de l'électroscope lorsqu'on approche un objet chargé positivement du sommet de celui-ci.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

26
Un électron qui tourne autour d'un noyau, une Lune qui tourne autour d'une planète

✔ RAI/ANA : Construire un raisonnement

Le zoom est accessible dans la version Premium.

L'atome d'hydrogène est constitué d'un proton et d'un électron. Selon le modèle de l'atome établi par Rutherford, l'électron gravite autour du proton, à la manière de la Lune qui gravite autour de la Terre.

1. Identifier des arguments allant dans le sens du modèle planétaire de l'atome.

2. Identifier des arguments révoquant ce modèle.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

27
Atome d'hélium, F_{\mathrm{e}} et F_{\mathrm{g}}

✔ MATH : Vecteur

Un atome d'hélium 4 est noté _{2}^{4} \mathrm{He}.

1. Donner la composition de cet atome.

Un atome d'hélium possède un rayon approximatif de r= 31 pm.

2. En considérant le noyau comme ponctuel, calculer l'intensité de la force électrostatique exercée par un proton du noyau sur un des électrons du cortège électronique.

3. Sans souci d'échelle, représenter cette force sur un schéma.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

4. Calculer l'intensité de la force gravitationnelle de ce proton sur cet électron.

5. Calculer le rapport de ces deux intensités. Commenter.

Données

e= 1,602 \times 10^-19 C ;
k= 8,99 \times 10⁹ N·m²·C^-2 ;
m_{\text{nucléon}}= 1,67 \times 10^-27 kg ;
m_{\text{électron}}= 9,11 \times 10^-31 kg ;
G= 6,67 \times 10^-11 N·m²·kg^-2.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

28
Comprendre les attendus
Un ion cuivre \mathrm{Cu}^{2+}

✔ MATH : Calcul littéral

1. Donner la composition du noyau et du nuage électronique d'un ion cuivre \mathrm{Cu}^{2+}.

2. Calculer la charge électrique portée par cet ion.

3. Représenter les lignes du champ électrostatique créé par cet ion, modélisé par un point.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

4. Calculer l'intensité du champ électrostatique que cet ion engendre à 1,0 cm de lui.

5. Calculer l'intensité du champ gravitationnel que cet ion engendre à 1,0 cm.

Données

G= 6,67 \times 10^-11 N·m²·kg^-2 ;
k= 8,99 \times 10⁹ N·m²·C^-2 ;
e= 1,602 \times 10^-19 C ;
_{29}^{63} \mathrm{Cu}
m_{\text{nucléon}}= 1,67 \times 10^-27 kg ;
m_{\text{électron}}= 9,11 \times 10^-31 kg.

Détails du barème
TOTAL /7 pts

1 pt

1. Identifier le nombre de protons et de neutrons à partir de Z et A.

1 pt

1. Identifier le nombre d'électrons à partir de Z et de la formule de l'ion cuivre (II) \mathrm{Cu}^{2+}.

1 pt

2. Identifier le calcul, le réaliser avec la bonne unité et le nombre correct de chiffres significatifs.

1 pt

3. Représenter correctement des lignes de champ, bien orientées.

1,5 pt

4. Identifier et utiliser la relation E=k \cdot \dfrac{q}{d^{2}} avec la bonne unité et le nombre de chiffres significatifs corrects.

1,5 pt

5. Identifier et utiliser la relation g=G \cdot \dfrac{m}{d^{2}} avec la bonne unité et le nombre de chiffres significatifs corrects.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

29
Envol d'un avion

✔ RAI/ANA : Utiliser des observations pour répondre à une problématique

Le zoom est accessible dans la version Premium.

Les lignes de champ de vitesse autour d'une aile d'avion lors du vol sont représentées ci-dessus. Plus la vitesse est grande dans une zone spatiale, plus la pression y est petite, et inversement.

À l'aide des lignes de champ représentées, expliquer comment la forme d'une aile d'avion lui permet de voler.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

30
Cartographie d'un champ électrostatique

✔ MATH : Vecteur

Soit un objet portant une charge électrique égale à +45 C.

1. À l'aide du déplacement d'une charge d'essai q_{\mathrm{e}}= 1 C à des endroits pertinents, cartographier le champ électrostatique créé par l'objet précédent dans un périmètre de 10 m. Représenter les lignes de champ.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

2. Même question pour le champ créé par une charge électrique égale à -45 C.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

31
Expérience de Rutherford

✔ RAI/ANA : Utiliser des observations pour répondre à une problématique

Le zoom est accessible dans la version Premium.

Lors d'une expérience célèbre, Ernest Rutherford envoie des particules \alpha chargées positivement sur une fine feuille d'or. Il observe la répulsion violente d'un petit nombre d'entre elles vers l'arrière.

1. Représenter les forces électrostatiques mises en jeu au moment où une particule \alpha s'approche d'un noyau d'atome d'or.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

2. Identifier la propriété du noyau d'un atome identifiée ici par Rutherford.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

32
Deux billes de cuivre en QCM

✔ MATH : Calcul littéral

Le zoom est accessible dans la version Premium.

Soit deux billes de cuivre portant toutes deux une charge électrique égale à +100e, séparées de 10 cm. Si on éloigne ces billes à 20 cm l'une de l'autre, les forces électrostatiques qu'elles exercent l'une sur l'autre vont :

a. être multipliées par 2.

b. être divisées par 2.

c. être multipliées par 4.

d. être divisées par 4.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

33
Vecteurs force et champ électrostatique

✔ MATH : Vecteur

Soit une petite bille de cuivre à laquelle on a réussi à enlever 150 électrons et une bille en verre à laquelle on a réussi à donner 50 électrons, situées à 10 cm l'une de l'autre. Dans cet exercice, on choisit d'orienter le vecteur unitaire de la bille de cuivre vers la bille de verre.

1. Sans souci d'échelle, schématiser la situation.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

2. Déterminer les valeurs des forces électrostatiques F_{\mathrm{e}} (cuivre/verre) et F_{\mathrm{e}} (verre/cuivre).

3. Calculer E_{\text {cuivre}} (verre), l'intensité du champ électrostatique engendré par la bille de cuivre, à l'endroit où est située la bille de verre.

On déplace la bille en verre d'un angle de 35° vers le haut, de manière à ce que les deux billes soient toujours séparées de 10 cm.

4. Que peut-on dire concernant F_{\mathrm{e}} (cuivre/verre), F_{\mathrm{e}} (verre/cuivre) et E_{\text { cuivre }} (verre) ?

Donnée

k= 8,99 \times 10⁹ N·m²·C^-2.
e= 1,602 \times 10^-19 C ;

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

34
Copie d'élève à commenter

Proposer une justification pour chaque erreur relevée par le correcteur.

1.

Le zoom est accessible dans la version Premium.

2. La force électrostatique de q_{1}= 2e sur q_{2}= -e est deux fois ~~plus intense que la force~~ électrostatique de q_{2} sur q_{1}.

3. La force électrostatique de q_{1}= 2e sur q_{2}=e est donnée par : \vec{F}_{\text{e}}= ~~\color{red}\xcancel{\color{black}k \cdot \dfrac{(2e)^{2}}{d^{2}} \vec{e}_{x}}.~~

4. Un exemple de champ vectoriel est un champ de ~~température sur une carte météorologique.~~

5. Le rapport des intensités de la force gravitationnelle sur la force électrostatique peut être déterminé en faisant le calcul suivant : ~~\color{red}\xcancel{\color{black}\vec{F}_g(q2/q1)=\vec{F}_\text{e}(q1/q2)}.~~

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

35
Cohésion d'un cristal de sel

✔ MATH : Calcul littéral

Le zoom est accessible dans la version Premium.

Le sel de cuisine est appelé en chimie solide ionique de chlorure de sodium. On parle de solide ionique, car les liaisons mises en jeu sont des liaisons ioniques et non covalentes. On peut donc considérer que le chlore et le sodium sont présents dans ce solide sous forme ionique, soit \mathrm{Cl}^{-} et \mathrm{Na}^{+}.

Le zoom est accessible dans la version Premium.

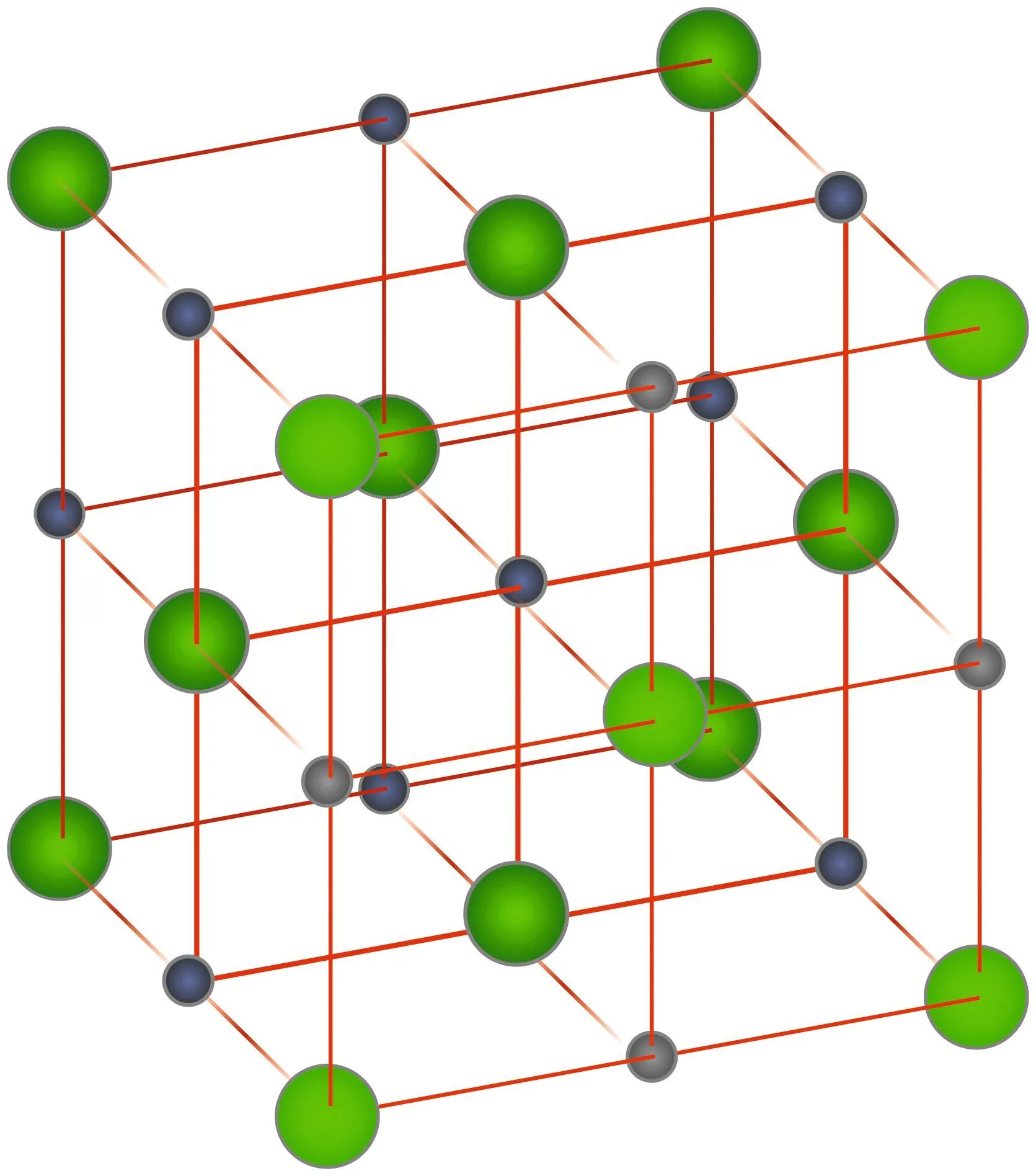
Une maille de ce cristal est représentée ci-dessus, les ions chlorure en vert et les ions sodium en bleu.
On remarque une alternance des ions sodium et chlorure : les voisins immédiats d'un ion sont de charge opposée.

1. À l'aide de cette dernière phrase, expliquer la cohésion d'un cristal ionique, engendrée par les forces électrostatiques mises en jeu.

On s'intéresse maintenant aux forces électrostatiques subies par un ion sodium.

2. Identifier le nombre d'ions chlorure les plus proches d'un ion sodium.

3. Identifier le nombre d'ions sodium les plus proches d'un ion sodium.

4. À l'aide de la maille représentée, calculer la distance d_{\mathrm{Na}-\mathrm{Cl}} entre les centres d'un ion sodium et un ion chlorure.

5. Calculer la valeur de la force électrostatique F(\mathrm{Cl}^{-} / \mathrm{Na}^{+}) exercée par un ion chlorure sur un ion sodium.

6. En appliquant le théorème de Pythagore, déterminer la distance d_{\mathrm{Na}-\mathrm{Na}} séparant deux ions sodium, en fonction de a.

7. Calculer la valeur de la force F(\mathrm{Na}^{+} / \mathrm{Na}^{+}) exercée par un ion sodium sur un autre ion sodium.

8. Les résultats des questions 5. et 7. confirment-ils la cohésion du cristal ?

Données

r(\mathrm{Na}^{+}) = 102 pm ;
r(\mathrm{Cl}^{-}) = 181 pm ;
a= 564 pm ;
e= 1,602 \times 10^-19 C ;
k= 8,99 \times 10⁹N·m²·C^-2.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

36
Observer Mars

✔ MATH : Calcul littéral

Le satellite MOM (Mars Orbiter Mission) a été lancé en novembre 2013. Il a pour objectif d'étudier l'atmosphère de Mars (R_{\text{Mars}} = 3,37 \times 10³ m). Il possède une masse d'environ 1 350 kg. Son orbite est représentée sur le schéma ci-dessous.

Le zoom est accessible dans la version Premium.

Calculer la différence des intensités des forces gravitationnelles exercées par Mars sur le satellite MOM lorsque ce dernier passe du point \text{A} au point \text{B.}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

37
La matière : du vide et des charges

✔ RAI/ANA : Construire un raisonnement

La matière est lacunaire, c'est-à-dire majoritairement constituée de vide. De plus, elle est constituée de particules neutres, les neutrons, ainsi que de particules chargées, les protons et les électrons.

1. Expliquer la cohésion de la matière par les interactions électrostatiques.

2. À l'aide des positions respectives des électrons et des protons au sein de l'atome, expliquer qu'un livre posé sur une table ne passe pas au travers de celle‑ci.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

38
La Lune s'éloigne

✔ MATH : Calcul littéral

Le zoom est accessible dans la version Premium.

La Lune s'éloigne chaque année de 3,8 cm de la Terre.

1. Cet éloignement influence-t-il la valeur de la force gravitationnelle qui s'exerce entre les deux astres ?

2. De quelle distance la Lune se sera-t-elle éloignée de la Terre dans 10 000 ans ?

3. Quelle sera alors la valeur de la force gravitationnelle entre les deux astres ?

Données

m_{\text{Terre}}= 6,0 \times 10²⁴ kg ;
m_{\text{Lune}}= 7,3 \times 10²² kg ;
d_{\text{Terre-Lune}}= 3,84 \times 10⁵ km ;
G= 6,67 \times 10^-11 N·m²·kg^-2.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Une règle, de la laine et un filet d'eau

✔ ANA : Utiliser des observations pour répondre à une problématique

On frotte une règle en plastique avec un morceau de laine. On approche ensuite la règle d'un filet d'eau, celui-ci se courbe.

1. Schématiser la répartition des charges électriques qui engendre la déviation du filet d'eau.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

Maintenant on approche le morceau de laine du filet d'eau et on observe le même phénomène qu'avec la règle.

2. Expliquer cela, puis schématiser la répartition des charges qui engendre cette nouvelle déviation.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Cage de Faraday

✔ ANA : Utiliser des observations pour répondre à une problématique

Une cage de Faraday est un dispositif couramment utilisé pour protéger les appareils électroniques des ondes électromagnétiques ou pour protéger des décharges les techniciens qui travaillent sur les lignes électriques.
Ces cages sont des enceintes métalliques qui vont permettre une isolation des champs électriques extérieurs.

Identifier la propriété, vue dans le cours, qui explique cette protection.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

C
Io

✔ ANA : Utiliser des observations pour répondre à une problématique

Io est un des satellites de Jupiter. Sa découverte est remarquable car elle a été faite par Galilée, au XVII^e siècle ! Dans cet exercice, on considère que la distance Io/Jupiter est négligeable devant la distance Jupiter/Soleil.

Déterminer entre le Soleil et Jupiter, l'astre dont l'action gravitationnelle est la plus forte sur Io :

en comparant les forces d'attraction gravitationnelle de ces deux astres sur Io

en comparant les deux champ gravitationnels de ces deux astres, sur la position de Io

Données

m_{Soleil} = 1{,}989 \times 10^{30} kg
m_{Jupiter} = 1{,}898 \times 10^{27} kg
m_{Io} = 8{,}9319 \times 10^{22} kg
d_{Io-Jupiter} = 4{,}2 \times 10^5 km
d_\text{Io-Soleil} = 7{,}8 \times 10^8 km

G = 6{,}67 \times 10^{-11} N·m²·kg^-2
k = 9{,}0 \times 10^9 N·m²·C^-2

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Pour s'entraîner

25Électroscope

26 Un électron qui tourne autour d'un noyau, une Lune qui tourne autour d'une planète

27Atome d'hélium, F_{\mathrm{e}} et F_{\mathrm{g}}

28Comprendre les attendus Un ion cuivre \mathrm{Cu}^{2+}

Détails du barème TOTAL /7 pts

29 Envol d'un avion

30 Cartographie d'un champ électrostatique

31Expérience de Rutherford

32Deux billes de cuivre en QCM

33 Vecteurs force et champ électrostatique

34Copie d'élève à commenter

35 Cohésion d'un cristal de sel

36 Observer Mars

37 La matière : du vide et des charges

38 La Lune s'éloigne

AUne règle, de la laine et un filet d'eau

BCage de Faraday

CIo

Une erreur sur la page ? Une idée à proposer ?

Nous préparons votre pageNous vous offrons 5 essais

25
Électroscope

26
Un électron qui tourne autour d'un noyau, une Lune qui tourne autour d'une planète

27
Atome d'hélium, F_{\mathrm{e}} et F_{\mathrm{g}}

28
Comprendre les attendus
Un ion cuivre \mathrm{Cu}^{2+}

Détails du barème
TOTAL /7 pts

29
Envol d'un avion

30
Cartographie d'un champ électrostatique

31
Expérience de Rutherford

32
Deux billes de cuivre en QCM

33
Vecteurs force et champ électrostatique

34
Copie d'élève à commenter

35
Cohésion d'un cristal de sel

36
Observer Mars

37
La matière : du vide et des charges

38
La Lune s'éloigne

A
Une règle, de la laine et un filet d'eau

B
Cage de Faraday

C
Io