Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 12
Entraînement 1
Variables aléatoires réelles
13 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
[Communiquer.]
Dans chaque cas, déterminer la valeur de p pour que le tableau soit celui d'une loi de probabilité.
1.
| x _ { i } | -2 | 1 | 3 |
| \text {P} \left( \text {X} = x_{i} \right) | \dfrac { 1 } { 3 } | \dfrac { 1 } { 2 } | p |
2.
| x _ { i } | -3 | 1 | 2 |
| \text {P} \left( \text {Y} = x_{i} \right) | 0,25 | p | 0,55 |
3.
| x _ { i } | -5 | -2 | 0 | 1 | 4 |
| \text {P} \left( \text {Z} = x_{i} \right) | p | \dfrac { 1 } { 4 } | \dfrac { 1 } { 6 } | \dfrac { 1 } { 6 } | \dfrac { 1 } { 3 } |
4.
| x _ { i } | -1 | 4 | 5 |
| \text {P} \left( \text {W} = x_{i} \right) | -2p+0\text{,}25 | p+0\text{,}25 | p+0\text{,}5 |
Aide
Quelle équation doit vérifier p ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On lance un dé tétraédrique équilibré dont les faces
sont numérotées de 1 à 4.
Dans chaque cas, déterminer :
1. les valeurs prises par la variable aléatoire \text{X} ;
2. la loi de probabilité de \text{X}.
1. les valeurs prises par la variable aléatoire \text{X} ;
2. la loi de probabilité de \text{X}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
[Modéliser.]
\text{X} est la variable aléatoire qui associe à chaque lancer le double du nombre obtenu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
[Modéliser.]
\text{X} est la variable aléatoire qui associe à chaque lancer l'inverse du nombre obtenu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
[Modéliser.]
\text{X} est la variable aléatoire qui associe à chaque lancer (-1)^n où n est le nombre obtenu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
[Modéliser.]
Une urne contient cinq boules indiscernables au toucher numérotées de 1 à 5. On en tire trois simultanément. Soit \text{M} la variable aléatoire qui associe au tirage de trois boules le plus petit nombre inscrit sur celles-ci.
1. Quelles sont les valeurs prises par \text{M ?}
2. Déterminer la loi de probabilité de \text{M.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
[Modéliser.]
Voici la composition d'un jeu de domino.
Le zoom est accessible dans la version Premium.
On tire au hasard un domino.
Soit \text{S} la variable aléatoire qui donne la somme des points inscrits sur le domino.
Déterminer la loi de probabilité de \text{S.}
Soit \text{S} la variable aléatoire qui donne la somme des points inscrits sur le domino.
Déterminer la loi de probabilité de \text{S.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
[Modéliser.]
Une urne contient les jetons, indiscernables au toucher, représentés ci-dessous.
Le zoom est accessible dans la version Premium.
1. Soit \text{X} la variable aléatoire qui associe, au tirage d'un jeton dans l'urne, la valeur du nombre inscrit sur
celui-ci. Déterminer la loi de probabilité de \text{X.}
2. On suppose maintenant que les jetons verts comptent double, les jetons rouges comptent pour moitié et les jetons bleus sont sans effet.
Soit \text{Y} la variable aléatoire qui associe, au tirage d'un jeton dans l'urne, la valeur du nombre inscrit sur celui-ci en tenant compte des modifications. Déterminer la loi de probabilité de \text{Y.}
2. On suppose maintenant que les jetons verts comptent double, les jetons rouges comptent pour moitié et les jetons bleus sont sans effet.
Soit \text{Y} la variable aléatoire qui associe, au tirage d'un jeton dans l'urne, la valeur du nombre inscrit sur celui-ci en tenant compte des modifications. Déterminer la loi de probabilité de \text{Y.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
[Modéliser.]On lance simultanément deux dés cubiques équilibrés dont les faces sont numérotées de 1 à 6.
1. Soit \text{S} la variable aléatoire qui associe à chaque lancer la somme des deux dés. Déterminer la loi de probabilité de \text{S.}
2. Soit \text{D} la variable aléatoire qui associe à chaque lancer la valeur absolue de la différence des deux dés. Déterminer la loi de probabilité de \text{D.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
[Modéliser.] Un jeu de tarot comporte 78 cartes :
- 56 cartes « classiques » (14 de chaque couleur : roi - dame - cavalier - valet - 10 - 9 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - as) ;
- 21 atouts (numérotés de 1 à 21) ;
- un joker appelé « excuse ».
Lors du comptage des points à la fin d'une partie, les cartes n'ont pas la même valeur :
- un roi, l'atout 1, l'atout 21 et l'excuse rapportent 4\text{,}5 points ;
- une dame rapporte 3\text{,}5 points ;
- un cavalier rapporte 2\text{,}5 points ;
- un valet rapporte 1\text{,}5 point ;
- toutes les autres cartes rapportent 0\text{,}5 point.
Soit \text{X} la variable aléatoire qui au tirage d'une carte d'un jeu de tarot associe sa valeur en points. Déterminer la loi de probabilité de \text{X.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
[Modéliser.] Lors d'une kermesse, dans un stand, sont disposées trois roues. Chaque roue est divisée en douze secteurs de même aire. Une roue étant lancée, elle s'arrête aléatoirement face à la flèche sur un seul secteur. On admettra que tous les secteurs ont la même probabilité d'être « tirés ».
Pour participer, un joueur choisit l'une des trois roues, acquitte la mise correspondant à la roue choisie, puis lance cette roue. Si le secteur « tiré » est jaune, le joueur reçoit le gain correspondant à la roue choisie.
Le zoom est accessible dans la version Premium.
Soit \text{X} (respectivement \text{Y} et \text{Z} ) la variable aléatoire donnant le gain du joueur qui lance la roue \text{R1} (respectivement \text{R2} et \text{R3} ). Déterminer la loi de probabilité de \text{X,} \text{Y} et \text{Z.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
[Modéliser.]
Le jeu de Scrabble est composé de 102 jetons : 2 jokers qui rapportent 0 point et les 26 lettres de l'alphabet sont réparties de la façon suivante.
Le zoom est accessible dans la version Premium.
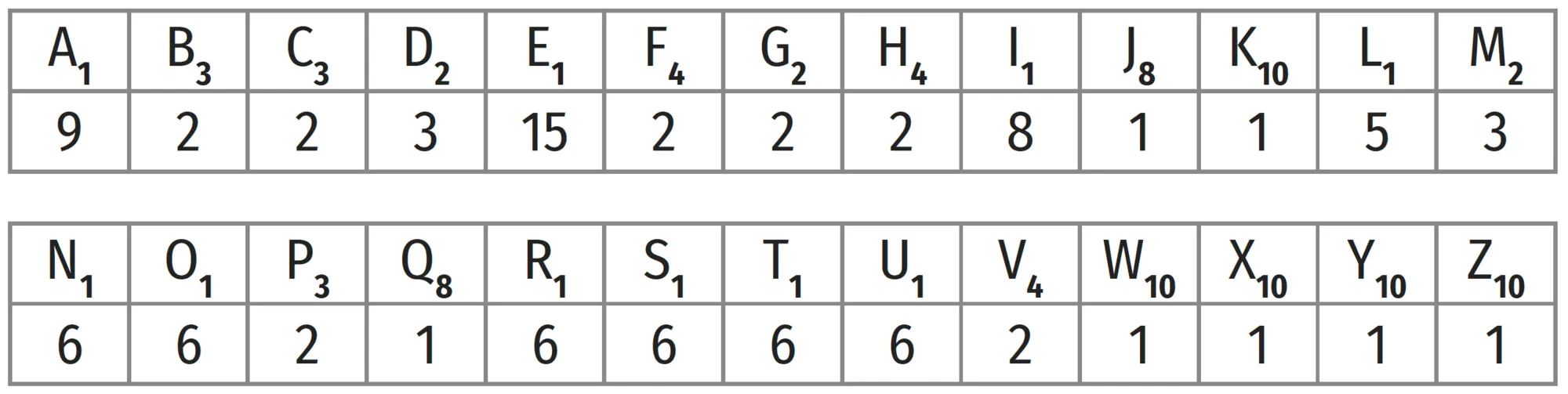
Par exemple, 9 jetons portent la lettre A et rapportent 1 point, 2 jetons portent la lettre B et rapportent 3 points, 2 jetons portent la lettre C et rapportent 3 points, etc.
Soit \text{X} la variable aléatoire qui associe au tirage d'un
jeton le nombre de points que celui-ci rapporte.
Déterminer la loi de probabilité de \text{X.}
Déterminer la loi de probabilité de \text{X.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
[Modéliser.]
Le jeu de Uno est composé de 108 cartes réparties de la
façon suivante :
- 76 cartes numérotées de 0 à 9 (19 de chacune des quatre couleurs, neuf paires de même valeur et un seul 0)\:;
- 32 cartes spéciales (huit cartes « inversion », huit cartes « passe ton tour », huit cartes « +2 », quatre cartes « +4 » et quatre cartes « joker »).
Le zoom est accessible dans la version Premium.
Soit \text{Y} la variable aléatoire qui au tirage d'une carte du jeu de Uno associe sa valeur en points. Déterminer la loi de probabilité de \text{Y.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
[Modéliser.]
Dans un club d'aviron, les adhérents peuvent choisir une formule d'entraînements uniquement le week-end, ou bien une formule d'entraînements le week-end et la semaine.
De plus, ils peuvent adhérer au club uniquement pour accéder à toutes les installations intérieures (rameurs, salle de musculation, etc.) sans profiter des entraînements sur l'eau.
Enfin, ils ont la possibilité de s'inscrire à des séances de fitness complémentaires.
La répartition des différents adhérents est donnée dans le tableau ci-après.
| Week-end uniquement | Week-end et semaine | En salle | Total | |
| Fitness | 20 | 70 | ||
| Pas fitness | 190 | 350 | ||
| Total | 150 | 450 |
1. Compléter le tableau à double entrée.
2. Le prix à l'année pour la formule week-end uniquement est de 450 \:€, 505\:€ pour la formule week-end et semaine, et 400\:€ pour la formule en salle. De plus, l'inscription aux séances de fitness coûte 30\:€ par an.
On note \text{X} le montant des frais d'inscription payés par un adhérent choisi au hasard dans ce club d'aviron. Donner la loi de probabilité de \text{X.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
Algo
[Modéliser.]
Une biscuiterie fabrique des cookies qu'elle conditionne en sachets. Les cookies peuvent être aux pépites de chocolat au lait, de chocolat noir ou de chocolat blanc et peuvent contenir ou non des éclats de noisettes.
Pour déterminer le prix \text{P} d'un sachet de cookies, la biscuiterie utilise l'algorithme suivant.
\boxed{
\begin{array} { l } { \text {P} \leftarrow \text {2,5} } \\
\text {Si les cookies sont aux pépites de chocolat noir :} \\
\quad \text{P} \leftarrow \text {P + 1} \\
\text {Sinon} : \\
\quad \text {Si les cookies sont aux pépites de chocolat blanc :} \\
\quad \quad \text{ P } \leftarrow \text { P + 0,5 } \\
\quad \text {Fin Si } \\
\text {Fin Si } \\
\text {Si les cookies ont des éclats de noisettes :} \\
\quad \text{P} \leftarrow \text {P + 0,5} \\
\text {Fin Si } \\
\end{array}
}
1. Déterminer le prix à payer pour un sachet de différentes variétés de cookies.
2. Les six types de cookies ont exactement la même probabilité d'être produits. On appelle \text{X} la variable aléatoire qui associe à un sachet de cookies son prix de vente. Déterminer la loi de probabilité de \text{X.}
2. Les six types de cookies ont exactement la même probabilité d'être produits. On appelle \text{X} la variable aléatoire qui associe à un sachet de cookies son prix de vente. Déterminer la loi de probabilité de \text{X.}
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
[Modéliser.]
On étudie le comportement d'une souris dans le labyrinthe ci-dessous.
Le zoom est accessible dans la version Premium.
À chaque intersection, la souris choisit au hasard et de manière équiprobable une direction. Soit \text{X} la variable aléatoire qui donne le nombre de fromages que la souris a mangés en traversant le labyrinthe. Déterminer la loi de probabilité de \text{X.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
[Modéliser.]
Un restaurant universitaire propose tous les jours de la viande ou du poisson avec comme accompagnement possible des frites ou du riz. On suppose que chaque étudiant choisit aléatoirement le contenu de son assiette.
Les prix affichés sont les suivants :
- viande : 4\text{,}50 € ;
- poisson : 3\text{,}50 € ;
- frites : 2 € ;
- riz : 3 €.
On note \text{T} la variable aléatoire donnant le prix payé pour un plat au restaurant universitaire. Déterminer la loi de probabilité de \text{T.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
[Chercher.]
La planche de Galton. Un joueur lâche une bille sur une planche inclinée sur laquelle sont plantés des clous comme sur la figure ci-dessous.
Le zoom est accessible dans la version Premium.
À chaque clou rencontré, la bille passe indifféremment à droite ou à gauche. En fin de parcours, elle tombe dans l'une des cases numérotées de 0 à 4. Le numéro de la case est donc le nombre de fois où la bille est descendue à droite lors de son parcours.
1. Traduire cette situation par un arbre de probabilité.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
2. Soit \text{X} la variable aléatoire qui au lancer d'une bille associe le numéro de la case dans laquelle elle termine son parcours. Déterminer la loi de probabilité de \text{X.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
[Modéliser.] Dans un zoo, on a regroupé dans le même enclos trois dromadaires (\text{D}_1, \text{D}_2 et \text{D}_3), deux chameaux (\text{C}_1 et \text{C}_2) et un lama (\text{L)}. Un visiteur prend en photo deux animaux qui ont tous la même probabilité d'être photographiés. Soit \text{X} la variable aléatoire donnant le nombre de bosses photographiées.
Déterminer la loi de probabilité de \text{X.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
[Modéliser.]
On choisit au hasard un nombre entier compris entre 1 et 20. Si c'est un nombre premier, on gagne 5\:€, si c'est un multiple de 4, on gagne 2\:€, sinon on perd 3\:€. Soit \text{X} la variable aléatoire donnant le gain du joueur.
Déterminer la loi de probabilité de \text{X.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
[Chercher.]
On lance un dé icosaédrique, dont les faces sont numérotées de 1 à 20, que l'on suppose bien équilibré.
On marque :
Les points sont cumulables.
Le zoom est accessible dans la version Premium.
On marque :
- 2 points si le nombre obtenu est pair ;
- 3 points si le nombre obtenu est premier ;
- 5 points si le nombre obtenu est un multiple de 5 ;
- 7 points si le nombre obtenu est un carré parfait.
Les points sont cumulables.
Soit \text{X} la variable aléatoire qui associe au lancer du dé
le nombre de points marqués par le joueur.
1. Déterminer la loi de probabilité de \text{X.}
2. En déduire \text{P}( \text{X} \leqslant 5 ), \text{P}( 3 \leqslant \text{X} \leqslant 7 ) et \mathrm { P } ( \mathrm { X } > 7 ).
1. Déterminer la loi de probabilité de \text{X.}
2. En déduire \text{P}( \text{X} \leqslant 5 ), \text{P}( 3 \leqslant \text{X} \leqslant 7 ) et \mathrm { P } ( \mathrm { X } > 7 ).
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah