Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 5
Cours 2
Extremums d'une fonction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AExtremum local
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Soient \text{I} un intervalle ouvert et c un réel de \text{I.} On considère une fonction f définie sur \text{I.} Dire que f(c) est un maximum local (respectivement minimum local) de f au voisinage de c signifie qu'il existe deux réels a et b dans \text{I} tels
que c \in ] a \:; b [ et, pour tout réel x de ] a\: ; b [, f ( x ) \leqslant f ( c ) (respectivement
f ( x ) \geqslant f ( c )).
Un extremum local est un maximum ou un minimum local.
Un extremum local est un maximum ou un minimum local.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On dit que f(c) est un maximum global sur \text{I} lorsque pour tout x \in \mathrm {I}, f ( x ) \leqslant f ( c ).
On définit de façon analogue un minimum global.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Soit une fonction h définie sur \R dont on donne la courbe représentative ci-dessous.
h(2) est un minimum local de h et h(1) = 2 est un maximum local de h.
h(-1) est un autre minimum local de h, il est aussi le minimum global de la fonction h.
Il ne semble pas y avoir de maximum global.
h(2) est un minimum local de h et h(1) = 2 est un maximum local de h.
h(-1) est un autre minimum local de h, il est aussi le minimum global de la fonction h.
Il ne semble pas y avoir de maximum global.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BLien avec la dérivation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Soient f une fonction dérivable sur un intervalle ouvert \text{I} et c un réel de \text{I.}
1. Si f(c) est un extremum local de f, alors f ^ { \prime } ( c ) = 0.


2. Si f ^ { \prime } s'annule en c en changeant de signe, alors f(c) est un extremum local de f.
1. Si f(c) est un extremum local de f, alors f ^ { \prime } ( c ) = 0.


2. Si f ^ { \prime } s'annule en c en changeant de signe, alors f(c) est un extremum local de f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Si f ^ { \prime } s'annule en c sans changer de signe, alors f(c) n'est pas un extremum.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Idées générales de la démonstration :
- Si f(c) est un extremum local, alors il y a un changement de variation au niveau du point c, d'où le changement de signe de la dérivée.
- De plus, la tangente à la courbe représentative de f au point d'abscisse c semble parallèle à l'axe des abscisses, d'où f ^ { \prime } ( c ) = 0 (voir l'illustration ci-dessus).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On peut affirmer que h ^ { \prime } ( - 1 ) = h ^ { \prime } ( 1 ) = h ^ { \prime } ( 2 ) = 0.
2. Soit f une fonction définie sur un intervalle [ a\: ; b ] et c \in [ a\: ; b ].
f(c) est un minimum local de f sur [ a\: ; b ]\::

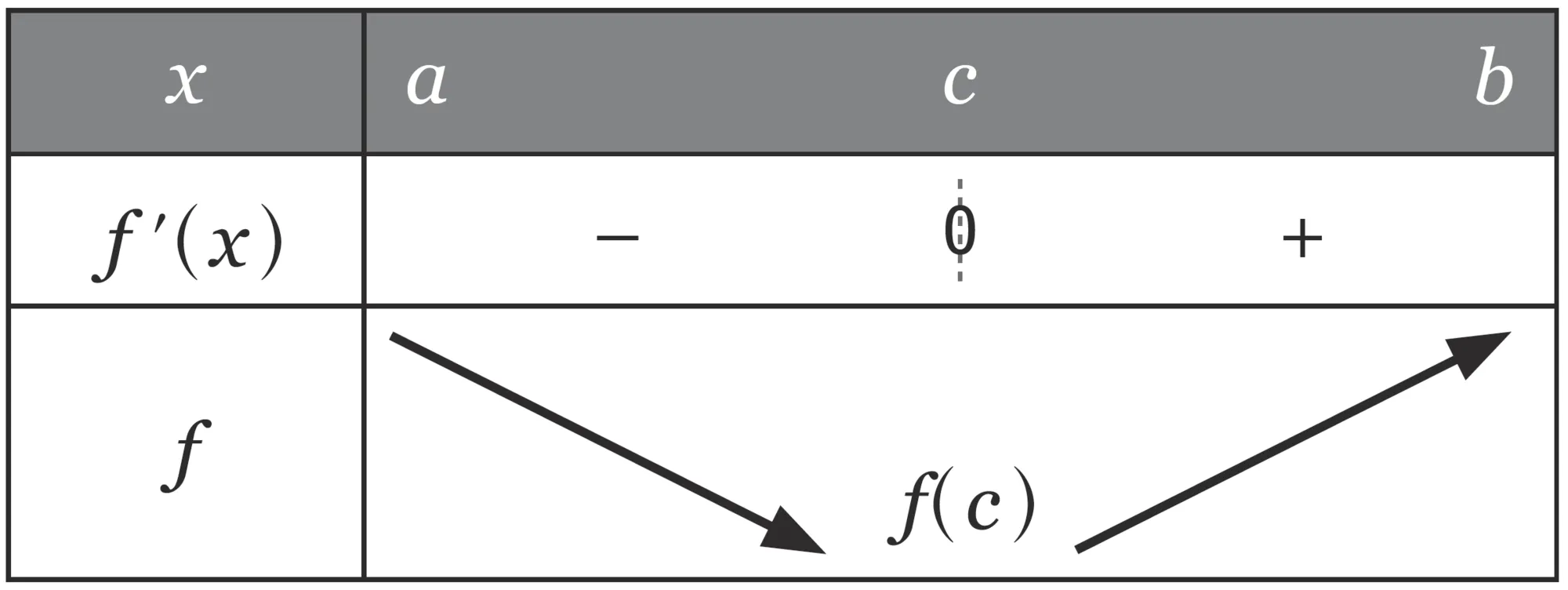


f(c) est un maximum local de f sur [ a\: ; b ]\::

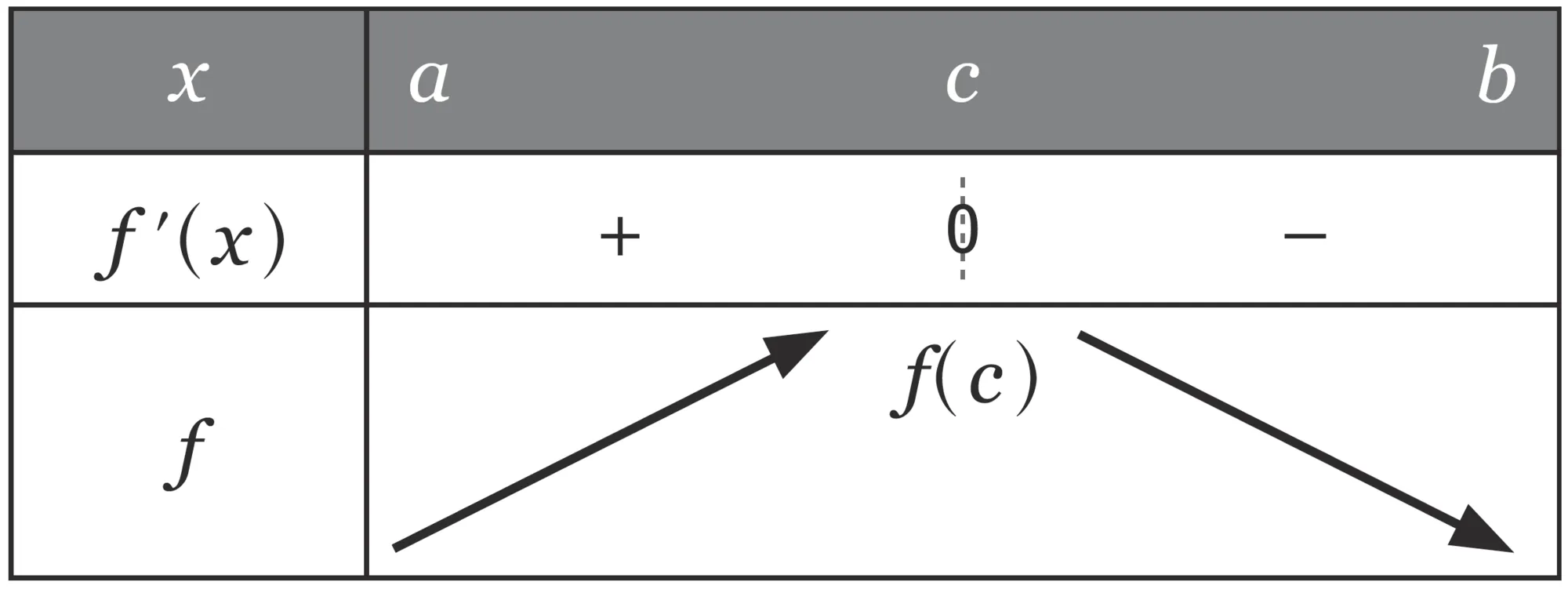


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On a représenté ci-dessous la fonction f définie sur [ - 2\: ; + \infty [ par
f ( x ) = - 0{,}5 x ^ { 3 } + 0{,}75 x ^ { 2 } + 3 x - 1.

1. Par lecture graphique, déterminer les valeurs de x pour lesquelles la fonction f semble admettre des extremums locaux.
2. a. Vérifier que la dérivée de f s'écrit sous la forme f ^ { \prime } ( x ) = - 1{,}5 ( x + 1 ) ( x - 2 ).
b. Étudier les variations de f, dresser son tableau de variations puis retrouver les résultats de la question 1..
b. Étudier les variations de f, dresser son tableau de variations puis retrouver les résultats de la question 1..
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. f semble admettre un minimum local pour x = -1 .
f semble admettre un maximum local pour x = 2 .
2. a. f est dérivable sur [-2\: ; 4] en tant que fonction polynôme et, pour tout x \in [ - 2 \:; 4 ] , f ^ { \prime } ( x ) = - 1{,}5 x ^ { 2 } + 1{,}5 x + 3.
On développe - 1{,}5 ( x + 1 ) ( x - 2 ) \: : on obtient l'expression de f ^ { \prime } ( x ).
b. On a f ^ { \prime } ( x ) = 0 \Leftrightarrow x = - 1 ou x = 2 .
En étudiant le signe de x + 1 et celui de x - 2 , on obtient le signe du produit.

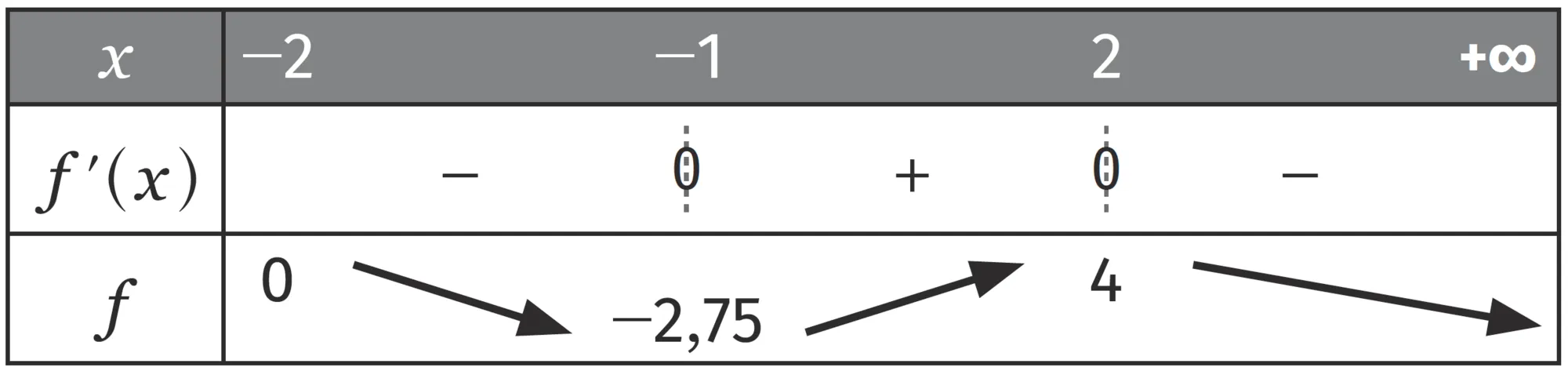
f ^ { \prime } s'annule en changeant de signe pour x = -1 et pour x = 2 .
-2{,}75 est un minimum local de f atteint pour x = -1 .
4 est un maximum local de f atteint pour x = 2 .
f semble admettre un maximum local pour x = 2 .
2. a. f est dérivable sur [-2\: ; 4] en tant que fonction polynôme et, pour tout x \in [ - 2 \:; 4 ] , f ^ { \prime } ( x ) = - 1{,}5 x ^ { 2 } + 1{,}5 x + 3.
On développe - 1{,}5 ( x + 1 ) ( x - 2 ) \: : on obtient l'expression de f ^ { \prime } ( x ).
b. On a f ^ { \prime } ( x ) = 0 \Leftrightarrow x = - 1 ou x = 2 .
En étudiant le signe de x + 1 et celui de x - 2 , on obtient le signe du produit.


f ^ { \prime } s'annule en changeant de signe pour x = -1 et pour x = 2 .
-2{,}75 est un minimum local de f atteint pour x = -1 .
4 est un maximum local de f atteint pour x = 2 .
Pour s'entraîner
exercices et p. 143 et p. 148
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour déterminer les extremums d'une fonction :
Graphiquement
1. on regarde où se trouvent les changements de variations ;
2. la valeur d'un extremum se lit sur l'axe des ordonnées.
Algébriquement
1. on vérifie que la fonction est dérivable et on calcule sa dérivée ;
2. on détermine les valeurs de x pour lesquelles la dérivée s'annule en changeant de signe ;
3. on en déduit les extremums en lisant les images des valeurs obtenues à l'étape précédente.
Graphiquement
1. on regarde où se trouvent les changements de variations ;
2. la valeur d'un extremum se lit sur l'axe des ordonnées.
Algébriquement
1. on vérifie que la fonction est dérivable et on calcule sa dérivée ;
2. on détermine les valeurs de x pour lesquelles la dérivée s'annule en changeant de signe ;
3. on en déduit les extremums en lisant les images des valeurs obtenues à l'étape précédente.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
