Exercices de synthèse

91

Devoir maison

[Calculer, Raisonner.]
D'après bac S, Centres étrangers, juin 2003

Soit (u_n) la suite définie, pour tout entier n \geqslant 1, par u_{n}=\frac{n^{2}}{2^{n}}.

1. Pour tout entier n \geqslant 1, on pose v_{n}=\frac{u_{n+1}}{u_{n}}.
a. Montrer que \lim\limits_{\substack{n \to +\infty}} v_{n}=\frac{1}{2}.

b. Montrer que, pour tout entier n \geqslant 1, v_{n}>\frac{1}{2}.

c. Déterminer le plus petit entier n_0 tel que, pour tout n \geqslant n_0, v_{n} \leqslant \frac{3}{4}.

d. En déduire que, pour tout n \geqslant n_0, u_{n+1} \leqslant \frac{3}{4} u_{n}.

2. Pour tout entier n \geqslant 5 on pose \mathrm{S}_{n}=\mathop{\sum}\limits_{k=5}\limits^{n} u_{k}=u_{5}+u_{6}+\ldots+u_{n}.

a. Montrer par récurrence que, pour tout entier n \geqslant 5 :

u_{n} \leqslant\left(\frac{3}{4}\right)^{n-5} u_{5}.

b. Montrer que, pour tout entier n \geqslant 5 :

\mathrm{S}_{n} \leqslant\left[1+\frac{3}{4}+\left(\frac{3}{4}\right)^{2}+\ldots+\left(\frac{3}{4}\right)^{n-5}\right] u_{5}.

c. En déduire que, pour tout entier n \geqslant 5, \mathrm{S}_{n} \leqslant 4 u_{5}.

3. Montrer que la suite (\text{S}_n) est croissante et en déduire qu'elle converge.

92

[Chercher, Communiquer.]
D'après bac S, Nouvelle Calédonie, novembre 2013

Suites mêlées

Soient (u_n) et (v_n) deux suites définies par u_0=2, v_0=10 et, pour tout entier naturel n :

1. a. Montrer que, pour tout entier naturel n : v_{n+1}-u_{n+1}=\frac{5}{12}\left(v_{n}-u_{n}\right).

b. Pour tout entier naturel n, on pose w_{n}=v_{n}-u_{n}.
Montrer que, pour tout entier naturel n, w_{n}=8\left(\frac{5}{12}\right)^{n}.

2. a. Montrer que la suite (u_n) est croissante et que la suite (v_n) est décroissante.

b. Montrer que, pour tout entier naturel n, on a : u_{n} \leqslant 10 et v_{n} \geqslant 2.

c. En déduire que les suites (u_n) et (v_n) convergent.

3. Montrer que les suites (u_n) et (v_n) ont la même limite.

4. a. Montrer que la suite (t_n) définie, pour tout entier naturel n, par t_{n}=3 u_{n}+4 v_{n} est constante.

b. En déduire que la limite commune des suites (u_n) et (v_n) est \frac{46}{7}.

93

[Raisonner, Calculer.]
Soient \left(\mathrm{S}_{n}\right) et \left(\mathrm{T}_{n}\right) deux suites définies, pour tout entier naturel n, par :
\mathrm{S}_{n}=\mathop{\sum}\limits_{k=0}\limits^{n} \frac{1}{3^{k}}=1+\frac{1}{3}+\ldots+\frac{1}{3^{n}} et \mathrm{T}_{n}=\mathop{\sum}\limits_{k=0}\limits^{n} \frac{k}{3^{k}}=\frac{1}{3}+\frac{2}{3^{2}}+\ldots+\frac{n}{3^{n}}.

1. a. Pour tout entier naturel n, exprimer \text{S}_n en fonction de n.

b. En déduire \lim\limits_{\substack{n \to +\infty}}\mathrm{S}_{n}.

2. a. Montrer que la suite \mathrm{T}_{n} est croissante.

b. Montrer que, pour tout entier naturel n, \mathrm{T}_{n+1}=\frac{\mathrm{S}_{n}+\mathrm{T}_{n}}{3}.

c. Montrer par récurrence que, pour tout entier n \geqslant 1, \mathrm{T}_{n} \leqslant 1.

d. En déduire que la suite \mathrm{T}_{n} converge vers un réel \ell.

e. On admet que \ell vérifie \ell=\frac{\ell+\frac{3}{2}}{3}. Déterminer \ell.

94

[Calculer, Modéliser.]
D'après bac S, Centres étrangers, juin 2018

Un détaillant en fruits et légumes étudie l'évolution de ses ventes de melons afin de pouvoir anticiper ses commandes.
Le détaillant réalise une étude sur ses clients. Il constate que :

• parmi les clients achetant un melon une semaine donnée, 90 % d'entre eux achètent un melon la semaine suivante ;
• parmi les clients n'achetant pas de melon une semaine donnée, 60 % d'entre eux n'achètent pas de melon la semaine suivante.

On choisit au hasard un client ayant acheté un melon au cours de la semaine 1 et, pour n \geqslant 1, on note \text{A}_n l'événement : « le client achète un melon au cours de la semaine n » et p_{n}=\mathrm{P}\left(\mathrm{A}_{n}\right). On a ainsi p_{1}=1.

1. Démontrer que, pour tout entier n \geqslant 1, p_{n+1}=0,5 p_{n}+0,4.

2. a. Montrer par récurrence que, pour tout entier n \geqslant 1, p_{n}>0,8.

b. Démontrer que la suite (p_n) est décroissante.

c. La suite (p_n) est‑elle convergente ?

3. On pose pour tout entier n \geqslant 1, v_{n}=p_{n}-0,8.
a. Démontrer que (v_n) est une suite géométrique dont on donnera le premier terme v_1 et la raison.

b. Exprimer v_n en fonction de n. En déduire que, pour tout n \geqslant 1, p_{n}=0,8+0,2 \times 0,5^{n-1}.

c. Déterminer la limite de la suite (p_n).

95

[Calculer, Communiquer.]

Suite arithmético-géométrique

Soient a et b deux réels tels que a \neq 0, a \neq 1 et b \neq 0.
On considère la suite (u_n) de premier terme u_{0} \in \mathbb{R} et définie, pour tout entier naturel n, par u_{n+1}=a u_{n}+b.

1. Résoudre dans \mathbb{R} l'équation x=a x+b.

On note \alpha la solution de cette équation.

2. Montrer que la suite (v_n) définie, pour tout entier naturel n, par v_{n}=u_{n}-\alpha est géométrique.

3. Exprimer alors v_n et u_n en fonction de u_0, n, a et b.

4. Suivant les valeurs de a, discuter de la convergence de la suite (u_n).

96

[Calculer, Modéliser.]
D'après bac S, Polynésie, juin 2018

Un lapin se déplace dans un terrier composé de trois galeries, notées \text{A}, \text{B} et \text{C}, dans chacune desquelles il est confronté à un stimulus particulier. À chaque fois qu'il est soumis à un stimulus, le lapin reste dans la galerie où il se trouve ou change de galerie. Cela constitue une étape.
Pour tout entier naturel n, on note a_n (respectivement b_n et c_n) la probabilité de l'événement : « Le lapin est dans la galerie \text{A} (respectivement \text{B} et \text{C}) à l'étape n ».
À l'étape n=0, le lapin est dans la galerie \text{A}.

Une étude antérieure des réactions du lapin face aux différents stimuli permet de modéliser ses déplacements par le système suivant :

L'objectif de cet exercice est d'estimer dans quelle galerie le lapin a la plus grande probabilité de se trouver à long terme.

1. Pour tout entier naturel n, on pose u_{n}=a_{n}-c_{n}.
a. Démontrer que la suite (u_n) est géométrique en précisant sa raison.

b. Exprimer u_n en fonction de n.

2. Pour tout entier naturel n, on pose v_{n}=b_{n}-\frac{4}{7}.
a. Expliquer pourquoi, pour tout entier naturel n, a_{n}+b_{n}+c_{n}=1 et en déduire que, pour tout entier naturel n, v_{n+1}=-\frac{1}{6} v_{n}.

b. Exprimer v_n en fonction de n.

3. En déduire que pour tout entier naturel n, on a :
a_{n}=\frac{3}{14}+\frac{1}{2}\left(\frac{1}{3}\right)^{n}+\frac{2}{7}\left(-\frac{1}{6}\right)^{n}, b_{n}=\frac{4}{7}-\frac{4}{7}\left(-\frac{1}{6}\right)^{n} et c_{n}=\frac{3}{14}-\frac{1}{2}\left(\frac{1}{3}\right)^{n}+\frac{2}{7}\left(-\frac{1}{6}\right)^{n}.

4. Que peut‑on en déduire sur la position du lapin après un très grand nombre d'étapes ?

97

[Représenter.]
D'après bac S, Polynésie, septembre 2017

Au début de l'an 2000, on comptait 300 tortues vivant sur une île.
Une étude a permis de modéliser ce nombre de tortues par la suite (u_n) définie par u_0=0{,}3 et, pour tout entier naturel n, u_{n+1}=0{,}9 u_{n}\left(1-u_{n}\right) où, pour tout entier naturel n, u_n modélise le nombre de tortues, en milliers, au début de l'année 2000+ n.

1. Calculer, dans ce modèle, le nombre de tortues au début de l'année 2001 puis de l'année 2002.

2. On admet que, pour tout entier naturel n, u_n et 1-u_n appartiennent à l'intervalle [0 ; 1].
a. Montrer que, pour tout entier naturel n : 0 \leqslant u_{n+1} \leqslant 0{,}9 u_{n}.

b. Montrer que, pour tout entier naturel n : 0 \leqslant u_{n} \leqslant 0{,}3 \times 0{,}9^{n}.

c. Déterminer la limite de la suite (u_n). Que peut‑on en conclure sur le devenir de cette population de tortues ?

3. Des études permettent d'affirmer que si le nombre de tortues à une date donnée est inférieur au seuil critique de 30 individus, alors l'espèce est menacée d'extinction.
On souhaite qu'à la fin de son exécution, l'algorithme ci contre calcule la dernière année avant laquelle il restera au moins 30 tortues. Recopier et compléter cet algorithme afin qu'il satisfasse cette exigence.

98

[Représenter, Modéliser.]
D'après bac S, Amérique du Nord, mai 2018

Un scooter radiocommandé se déplace en ligne droite à la vitesse constante de 1 m·s⁻¹. Il est poursuivi par un chien qui se déplace à la même vitesse.
On représente la situation vue de dessus dans un repère orthonormé du plan d'unité 1 mètre. L'origine de ce repère est la position initiale du chien. Le scooter est représenté par un point appartenant à la droite d'équation x = 5. Il se déplace sur cette droite dans le sens des ordonnées croissantes.
La situation est représentée par le graphique ci‑dessous.

À l'instant initial, le scooter est représenté par le point \text{S}_0. Le chien qui le poursuit est représenté par le point \text{M}_0. On considère qu'à chaque seconde, le chien s'oriente instantanément en direction du scooter et se déplace en ligne droite sur une distance de 1 mètre.
Ainsi, à l'instant initial, le chien s'oriente en direction du point \text{S}_0, et une seconde plus tard il se trouve un mètre plus loin au point \text{M}_1.
À cet instant, le scooter est au point \text{S}_1. Le chien s'oriente en direction de \text{S}_1 et se déplace en ligne droite en parcourant 1 mètre, et ainsi de suite.
On modélise alors les trajectoires du chien et du scooter par deux suites de points notées (\text{M}_n) et (\text{S}_n).
Au bout de n secondes, les coordonnées du point \text{S}_n sont (5 ; n).
On note (x_n ; y_n) les coordonnées du point \text{M}_n.

1. Reproduire le graphique et construire les points \mathrm{M}_{2} et \mathrm{M}_{3}.


2. On note d_n la distance entre le chien et le scooter n secondes après le début de la poursuite.
On a donc d_{n}=\mathrm{M}_{n} \mathrm{S}_{n}.
Calculer d_0 et d_1.

3. Justifier que le point \mathrm{M}_{2} a pour coordonnées : \left(1+\frac{4}{\sqrt{17}} ; \frac{1}{\sqrt{17}}\right).

4. On admet que, pour tout entier naturel n :

a. Le tableau ci‑dessous, obtenu à l'aide d'un tableur, donne les coordonnées des points \mathrm{M}_{n} et \mathrm{S}_{n} ainsi que la distance d_n en fonction de n.


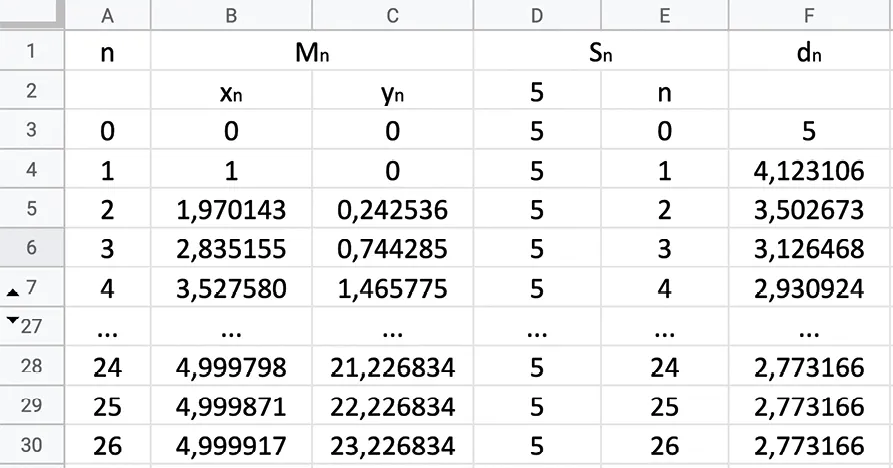
Quelles formules doit‑on écrire dans les cellules B4, C4 et F4 et recopier vers le bas pour remplir les colonnes B, C et F ?

b. On admet que la suite (d_n) est strictement décroissante. Justifier que cette suite est convergente et conjecturer sa limite à l'aide du tableau.

100

Approfondissement

Deux suites (u_n) et (v_n) définies pour tout entier naturel n sont dites adjacentes lorsque l'une est croissante, l'autre est décroissante et que \lim\limits_{\substack{n \to +\infty}}\left(u_{n}-v_{n}\right)=0. Nous allons démontrer que si (u_n) et (v_n) sont deux suites adjacentes, alors elles convergent et elles ont toutes les deux la même limite. Pour cela, considérons deux suites (u_n) et (v_n) telles que, quitte à inverser les rôles, (u_n) est croissante, (v_n) est décroissante et \lim\limits_{\substack{n \to +\infty}}\left(u_{n}-v_{n}\right)=0.

1. a. Montrer que la suite \left(v_{n}-u_{n}\right) est décroissante.

b. En déduire que, pour tout entier naturel n, on a u_{n} \leqslant v_{n}.

2. Nous allons à présent montrer que (u_n) converge. a. Prouver que la suite (u_n) est majorée.

b. En déduire que la suite (u_n) converge.

Avec un raisonnement analogue, on montre de même que la suite (v_n) converge.

3. Nous allons à présent montrer que les deux suites convergent vers la même limite. Pour cela, notons \lim\limits_{\substack{n \to +\infty}} u_{n}=\ell et \lim\limits_{\substack{n \to +\infty}} v_{n}=\ell^{\prime}.
a. Grâce aux opérations sur les limites, déterminer \lim\limits_{\substack{n \to +\infty}}\left(u_{n}-v_{n}\right).

b. En déduire que \ell=\ell^{\prime}.

4. Soient (u_n) et (v_n) deux suites définies pour tout entier n \geqslant 1 par : u_{n}=\mathop{\sum}\limits_{k=0}\limits^{n} \frac{1}{k !}=\frac{1}{0 !}+\frac{1}{1 !}+\frac{1}{2 !}+\ldots+\frac{1}{n !} et v_{n}=u_{n}+\frac{1}{n ! \times n} où k !=1 \times 2 \times \ldots \times k et, par convention 0!=1.
a. Montrer que les suites (u_n) et (v_n) sont adjacentes.

b. Grâce à la calculatrice, déterminer une valeur approchée à 10^{-6} près de la limite commune de ces deux suites.

101

Approfondissement

Méthode de Newton

Soit f une fonction définie et dérivable sur un intervalle \text{I} et telle que f^{\prime} ne s'annule pas sur \text{I}. On note \mathcal{C }_f sa courbe représentative dans un repère orthogonal. On admet que l'équation f(x)=0 admet une unique solution \alpha sur \text{I} dont on cherche à déterminer une approximation. Soit x_0 un nombre réel de \text{I}.
Pour tout entier naturel n, x_{n+1} est l'abscisse du point d'intersection de l'axe des abscisses avec la tangente à \mathcal{C }_f au point d'abscisse x_n.

1. Montrer que, pour tout entier naturel n : x_{n+1}=x_{n}-\frac{f\left(x_{n}\right)}{f^{\prime}\left(x_{n}\right)}.

2. Soit f la fonction définie sur ] 0 ; +\infty[ par f(x)=x^{2}-2. On pose x_0=2.
a. Montrer que pour tout entier naturel n, on a : x_{n+1}=\frac{x_{n}^{2}+2}{2 x_{n}}.

b. Soit g la fonction définie sur ] 0 ;+\infty[ par g(x)=\frac{x^{2}+2}{2 x}. Étudier les variations de la fonction g.

c. Montrer par récurrence que, pour tout n \in \mathbb{N}, \sqrt{2} \leqslant x_{n+1} \leqslant x_{n}.

d. En déduire que la suite (x_n) converge vers un réel \ell.

e. On admet que \ell vérifie \ell=\frac{\ell^{2}+2}{2\ell}. Déterminer \ell.

3. Soit f la fonction définie sur [1 ;+\infty[ par f(x)=x^{2}-x-1. on pose x_0=2.
a. Résoudre l'équation x^{2}-x-1=0.
On note \Phi la solution positive de cette équation.

b. Montrer que pour tout entier naturel n, on a : x_{n+1}=\frac{x_{n}^{2}+1}{2 x_{n}-1}.

c. Soit g la fonction définie sur [1 ;+\infty[ par g(x)=\frac{x^{2}+1}{2 x-1}. Étudier les variations de la fonction g.

d. Montrer par récurrence que, pour tout n \in \mathbb{N}, \Phi \leqslant x_{n+1} \leqslant x_{n}.

e. En déduire que la suite (x_n) converge vers un réel \ell.

f. On admet que \ell vérifie \ell=\frac{\ell^{2}+1}{2 \ell-1}. Montrer que \ell=\Phi.

102

Approfondissement

Méthode de Héron

Soit a un nombre réel strictement positif.
Considérons la suite (u_n) définie par \left.u_{0} \in\right] 0 ;+\infty[ et, pour tout entier naturel n, u_{n+1}=\frac{1}{2}\left(u_{n}+\frac{a}{u_{n}}\right).

1. Montrer par récurrence que la suite (u_n) est positive.

2. a. Montrer que, pour tout entier naturel n : u_{n+1}-\sqrt{a}=\frac{\left(u_{n}-\sqrt{a}\right)^{2}}{2 u_{n}}.

b. En déduire que, pour tout entier naturel n \geqslant 1 : u_{n}-\sqrt{a} \geqslant 0.

c. Montrer que la suite (u_n) est décroissante.

3. En déduire que la suite (u_n) converge vers un réel \ell.

4. On admet que \ell vérifie \ell=\frac{1}{2}\left(\ell+\frac{a}{\ell}\right). Déterminer la valeur de \ell.

103

Approfondissement

Suites récurrentes linéaires d'ordre deux

Une suite (u_n) définie sur \mathbb{N} est une suite récurrente linéaire d'ordre deux lorsqu'il existe deux réels a et b avec b non nul tels que, pour tout entier n, u_{n+2}=a u_{n+1}+b u_{n}.
Pour une telle suite, on appelle (\mathrm{E}): r^{2}=a r+b l'équation caractéristique.
Dans la suite, (u_n) désignera une suite récurrente linéaire d'ordre deux de premiers termes u_0 et u_1.

Partie A

On suppose dans cette partie que l'équation (\mathrm{E}) admet deux solutions réelles distinctes r_1 et r_2.
On va montrer que, pour une telle suite, il existe deux uniques nombres réels \lambda et \mu tels que, pour tout n \in \mathbb{N}, u_{n}=\lambda r_{1}^{n}+\mu r_{2}^{n}.

1. On suppose que, pour tout n \in \mathbb{N}, u_{n}=\lambda r_{1}^{n}+\mu r_{2}^{n}.
Calculer \lambda et \mu en fonction de u_0, u_1, r_1 et r_2.

2. Pour tout entier naturel n, on note \mathrm{P}(n) la proposition u_{n}=\lambda r_{1}^{n}+\mu r_{2}^{n}.
a. Vérifier que \mathrm{P}(0) et \mathrm{P}(1) sont vraies.

b. Soit k un entier naturel tel que \mathrm{P}(k) et \mathrm{P}(k+1) sont vraies. Montrer alors que \mathrm{P}(k+2) est également vraie.

c. En déduire que \mathrm{P}(n) est vraie pour tout entier naturel n puis conclure.

3. Application : On appelle suite de Fibonacci la suite (u_n) définie par u_{0}=u_{1}=1 et la relation, valable pour tout entier naturel n, u_{n+2}=u_{n+1}+u_{n}.
Écrire l'équation caractéristique associée, la résoudre, puis exprimer, pour tout entier naturel n, u_n en fonction de n.

Partie B

On suppose dans cette partie que l'équation (\mathrm{E}) admet une unique solution r_0.
On va montrer que, pour une telle suite, il existe deux uniques nombres réels \lambda et \mu tels que, pour tout n \in \mathbb{N}, u_{n}=\lambda r_{0}^{n}+\mu n r_{0}^{n}.

1. Montrer que dans ce cas, l'équation (\mathrm{E}) peut s'écrire r^{2}=2 r_{0} r-r_{0}^{2}.

2. On suppose que, pour tout n \in \mathbb{N}, u_{n}=\lambda r_{0}^{n}+\mu n r_{0}^{n}.
Calculer \lambda et \mu en fonction de u_0, u_1, r_0.

3. Pour tout entier naturel n, on note \mathrm{P}(n) la proposition u_{n}=\lambda r_{0}^{n}+\mu n r_{0}^{n}.
Montrer, en utilisant un raisonnement analogue à celui rencontré dans la Partie A, que \mathrm{P}(n) est vraie pour tout entier naturel n.

4. Application : Soit (u_n) la suite définie par u_0=4, u_1=3 et la relation, valable pour tout entier naturel n, u_{n+2}=4 u_{n+1}-4 u_{n}.
Écrire l'équation caractéristique associée, la résoudre, puis exprimer, pour tout entier naturel n, u_n en fonction de n.

Méthode

❯ Vous avez travaillé pendant des semaines sur votre oral, vous avez appris énormément de choses, vous avez envie de tout dire… Or, votre présentation ne doit pas durer plus de 5 minutes ! Vous devez aller à l'essentiel : cela nécessite de faire des choix.

❯ Au brouillon, notez toutes vos idées, sous la forme de mots‑clés ou de phrases ; organisez‑les ensuite par grandes thématiques. Ces thématiques vont constituer la trame de votre présentation.

❯ Vous pouvez noter le niveau de priorité en face de chaque point que vous voulez aborder : priorité 1 (à évoquer absolument), priorité 2 (important à évoquer), priorité 3 (moins important, à évoquer s'il reste du temps). Cela vous aidera à hiérarchiser vos idées.

Exemples de points à aborder

❯ Il peut être judicieux de commencer par donner quelques éléments biographiques rapides sur Fibonacci.

❯ Expliquer comment est définie cette suite sera une étape essentielle de votre développement. Vous pouvez commencer par présenter les suites récurrentes linéaires d'ordre 1 avant d'aborder les suites récurrentes linéaires d'ordre 2.

❯ La suite de Fibonacci possède de très nombreuses propriétés (la limite des quotients de ses termes est liée au nombre d'or, la recherche d'un maximum par méthode dichotomique, l'approximation de la spirale logarithmique, etc.). Il faut choisir celles que vous souhaitez aborder car vous n'aurez pas le temps de tout traiter.

Méthodologie

Consulter les fiches méthode de ce manuel pour le Grand Oral p. 14