Mathématiques Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme n�épérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 13
TP INFO 2
Le paradoxe du duc de Toscane
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Grand habitué des jeux de dés, le duc de Toscane aurait remarqué qu'en lançant trois dés équilibrés et en faisant la somme des trois nombres obtenus, la somme 10 était plus fréquente que la somme 9 alors qu'il y a autant de manières d'écrire 9 que 10 en faisant la somme de trois entiers compris entre 1 et 6.
Questions préliminaires :
1. Avec trois dés, on peut obtenir la somme 9 de la façon suivante : 1 + 2 + 6.
Trouver les cinq autres possibilités d'obtenir la somme 9.
2. Trouver les six possibilités d'obtenir la somme 10 avec trois dés.
1. Avec trois dés, on peut obtenir la somme 9 de la façon suivante : 1 + 2 + 6.
Trouver les cinq autres possibilités d'obtenir la somme 9.
2. Trouver les six possibilités d'obtenir la somme 10 avec trois dés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
On cherche à vérifier expérimentalement
la conjecture du duc de Toscane à l'aide
d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1 Tableur
1.
Reproduire la feuille de calcul ci‑dessous dans un tableur.

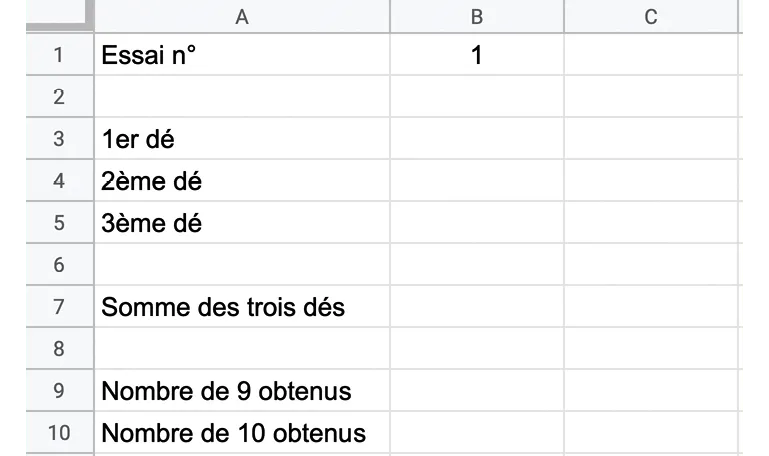
2. On souhaite faire 200 essais de lancers de triplets de dés équilibrés. Qu'écrire en case C1 ? Étendre la formule jusqu'à la case GS1.


2. On souhaite faire 200 essais de lancers de triplets de dés équilibrés. Qu'écrire en case C1 ? Étendre la formule jusqu'à la case GS1.
3.
Simuler le lancer de chacun des trois dés aux lignes 3, 4 et 5.
4. Remplir les cases de la ligne 7.
5. Remplir enfin les lignes 9 et 10.
6. Comparer le résultat obtenu avec celui des autres élèves de la classe. Retrouve‑t‑on expérimentalement l'hypothèse du duc de Toscane ?
Aide
On pourra utiliser la commande ALEA.ENTRE.BORNES
4. Remplir les cases de la ligne 7.
Aide
On pourra utiliser la commande SOMME.
5. Remplir enfin les lignes 9 et 10.
Aide
On pourra utiliser la commande NB.SI.
6. Comparer le résultat obtenu avec celui des autres élèves de la classe. Retrouve‑t‑on expérimentalement l'hypothèse du duc de Toscane ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
On considère le programme suivant.
from random import *
def somme_des_dés():
dé_1 = randint(1,6)
dé_2 = randint(1,6)
dé_3 = randint(1,6)
S = dé_1 + dé_2 + dé_3
return S
def comparaison_10_et_9(n):
i = 0
j = 0
for k in range(n):
S = somme_des_dés()
if S == 10 :
i = i + 1
elif S == 9 :
j = j + 1
return (i,j)
1.
Expliquer la fonction somme_des_dés. À quoi sert‑elle ?
2. Les variables i et j correspondent à des variables de comptage (correspondant respectivement aux nombres de 10 et de 9 obtenus). Expliquer la suite du programme.
3. Tester le programme pour n = 10000.
Cela semble‑t‑il confirmer l'hypothèse du duc de Toscane ?
2. Les variables i et j correspondent à des variables de comptage (correspondant respectivement aux nombres de 10 et de 9 obtenus). Expliquer la suite du programme.
3. Tester le programme pour n = 10000.
Cela semble‑t‑il confirmer l'hypothèse du duc de Toscane ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour tout k \in\{1 \: ; 2 \: ; 3\}, on note \mathrm{X}_{k} la variable aléatoire
correspondant au résultat du k^{e} dé et \text{X} la
variable aléatoire correspondant à la somme alors
obtenue.
1. Exprimer \text{X} en fonction des variables aléatoires \mathrm{X}_{k}.
2. Calculer \mathrm{E}(\mathrm{X}). Déterminer alors \mathrm{V}(\mathrm{X}) et \sigma(\mathrm{X}).
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
