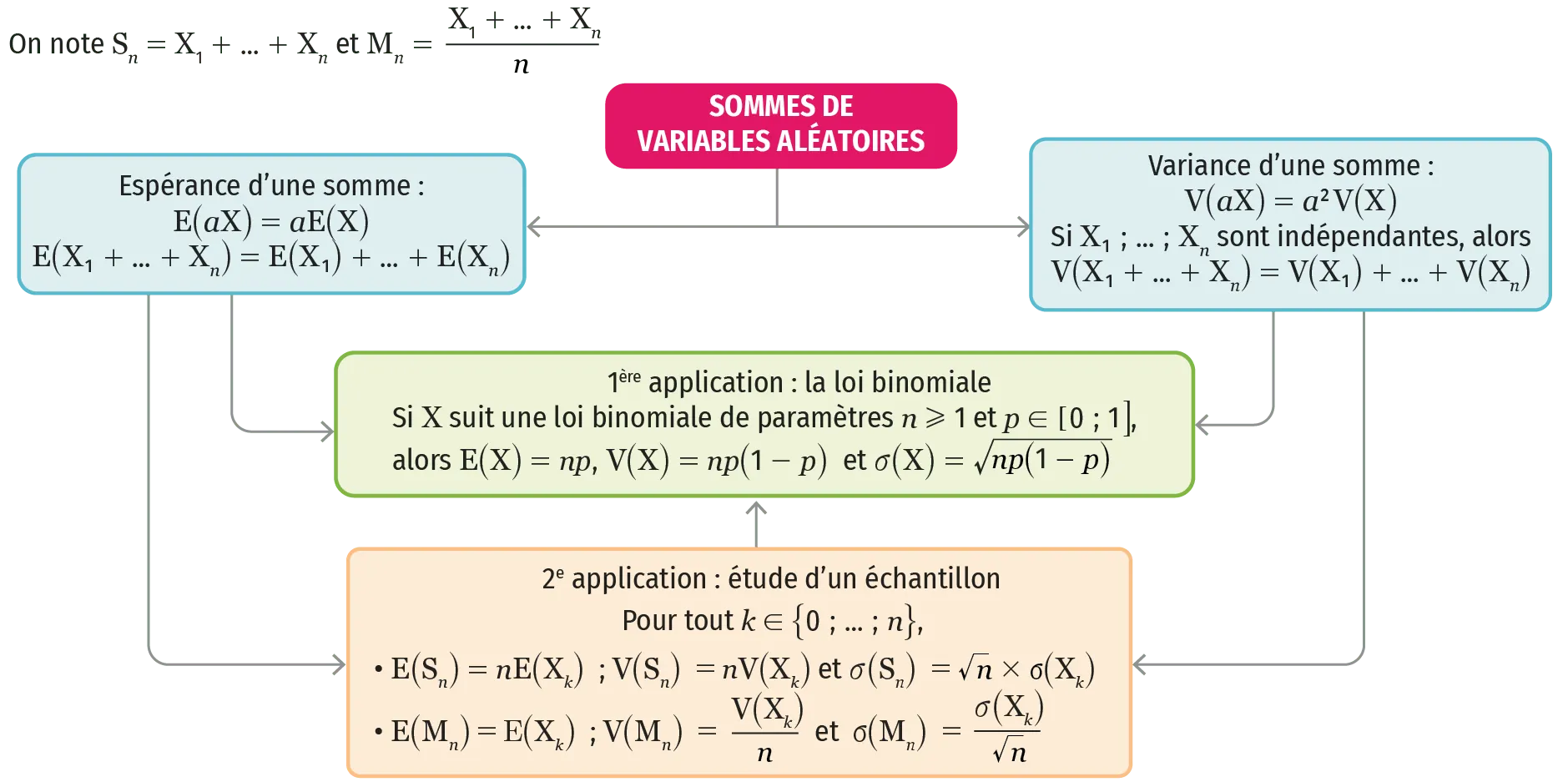
1

Si \textbf{X} et \textbf{Y} sont deux variables aléatoires définies sur un univers \Omega et si \boldsymbol{a} est un nombre réel, on a les égalités \mathbf{E}(\mathbf{X}+\mathbf{Y})=\mathbf{E}(\mathbf{X})+\mathbf{E}(\mathbf{Y}), \mathbf{E}(\boldsymbol{a} \mathbf{X})=\boldsymbol{a} \mathbf{E}(\mathbf{X}) \operatorname{et} \mathbf{E}(\boldsymbol{a} \mathbf{X}+\mathbf{Y})=\boldsymbol{a} \mathbf{E}(\mathbf{X})+\mathbf{E}(\mathbf{Y}). Cela permet de :

✔ déterminer l'espérance d'une variable aléatoire en la décomposant comme somme de variables aléatoires plus simples à étudier ;
✔ démontrer que si \text{X} suit la loi binomiale de paramètres n et p, alors \mathrm{E}(\mathrm{X})=n p.

2

Si \textbf{X} et \textbf{Y} sont deux variables aléatoires indépendantes définies sur un univers \Omega et si \boldsymbol{a} est un nombre réel, on a les égalités \mathbf{V}(\mathbf{X}+\mathbf{Y})=\mathbf{V}(\mathbf{X})+\mathbf{V}(\mathbf{Y}) \text { et } \mathbf{V}(\boldsymbol{a} \mathbf{X})=\boldsymbol{a}^{2} \mathbf{V}(\mathbf{X}).  :

✔ déterminer la variance d'une variable aléatoire en la décomposant comme somme de variables aléatoires indépendantes plus simples à étudier ;
✔ démontrer que si \text{X} suit la loi binomiale de paramètres n et p, alors \mathrm{V}(\mathrm{X})=n p(1-p) et \sigma(\mathrm{X})=\sqrt{n p(1-p)}.

3

Étude de la somme \mathbf{S}_{n} de n variables aléatoires indépendantes \mathbf{X}_{1} ; \ldots ; \mathbf{X}_{n} suivant la même loi de probabilité. La variable aléatoire \mathbf{S}_{n} s'écrit \mathbf{S}_{n}=\mathbf{X}_{1}+\ldots+\mathbf{X}_{n}. Cela permet de :

✔ étudier plus simplement les propriétés de la somme, notamment dans le cas de la répétition de n expériences dans des conditions indépendantes ;
✔ calculer l'espérance de \mathrm{S}_{n} en utilisant, pour tout k \in\{1 \: ; \ldots \: ; n\}, \mathrm{E}\left(\mathrm{S}_{n}\right)=n \mathrm{E}\left(\mathrm{X}_{k}\right) ;
✔ calculer l'espérance de \mathrm{S}_{n} en utilisant \mathrm{V}\left(\mathrm{S}_{n}\right)=n \mathrm{V}\left(\mathrm{X}_{k}\right). On a ainsi \sigma\left(\mathrm{S}_{n}\right)=\sqrt{n} \sigma\left(\mathrm{X}_{k}\right).

4

Étude de la moyenne \mathbf{M}_{n} de n variables aléatoires indépendantes \mathbf{X}_{1} ; \ldots ; \mathbf{X}_{n} suivant la même loi de probabilité. La variable aléatoire \mathbf{M}_{n} s'écrit \mathbf{M}_{n}=\frac{\mathbf{X}_{1}+\ldots+\mathbf{X}_{n}}{\mathbf{n}}. Cela permet de :

✔ étudier plus simplement les propriétés de la moyenne, notamment dans le cas de la répétition de n expériences dans des conditions indépendantes ;
✔ calculer l'espérance de \mathbf{M}_{n} en utilisant, pour tout k \in\{1 \: ; \ldots \: ; n\}, \mathrm{E}\left(\mathrm{M}_{n}\right)=\mathrm{E}\left(\mathrm{X}_{k}\right) ;
✔ calculer l'espérance de \mathbf{M}_{n} en utilisant V\left(M_{n}\right)=\frac{V\left(X_{k}\right)}{n}. On a ainsi \sigma\left(\mathrm{M}_{n}\right)=\frac{\sigma\left(\mathrm{X}_{k}\right)}{\sqrt{n}}.