Sommaire
Mes pages
N° Page
ouverture
p. 1-17
Algèbre
Rappelsp. 445-446
Algèbre et géométrie
Analyse
Probabilités
Annexes
/ 451
Page précédente
Chapitre 14
Activité

Loi des grands nombres

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Autour d'une inégalité

Objectif : Travailler autour de l'inégalité de Bienaymé-Tchebychev.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
On considère une urne contenant quatre boules noires et six boules blanches indiscernables au toucher. On tire successivement et sans remise des boules dans l'urne jusqu'à l'obtention d'une boule blanche. On note \text{X} le rang d'apparition de la première boule blanche.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
1
Déterminer toutes les valeurs de \text{X} puis donner sa loi de probabilité.

Cliquez pour accéder à une zone de dessin


2
À l'aide de la calculatrice, calculer l'espérance et la variance de \text{X} (donner une valeur approchée à 10^{-3} près).

3
Calculer \mathrm{P}(|\mathrm{X}-\mathrm{E}(\mathrm{X})| \geqslant 2) et comparer ce résultat à \frac{\text{V(X)}}{2^{2}}.
Aide
Déterminer les valeurs de \text{X} telles que l'inégalité |\mathrm{X}-\mathrm{E}(\mathrm{X})| \geqslant 2 est respectée.

4
Comparer \mathrm{P}(|\mathrm{X}-\mathrm{E}(\mathrm{X})| \geqslant 0{,}5) à \frac{\text{V(X)}}{0{,}5^{2}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Bilan
Conjecturer une généralisation de l'inégalité constatée dans cette activité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Une situation d'équiprobabilité

Objectif : Simuler une expérience dans un cas équiprobable et observer le comportement des valeurs obtenues.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
On lance une pièce de monnaie équilibrée et on souhaite observer la répartition du nombre de piles et de faces obtenu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
1
Écrire un programme en Python permettant de simuler n lancers d'une pièce de monnaie.
Faire afficher le nombre de piles et de faces obtenu. On privilégiera un programme contenant une fonction prenant comme argument n et renvoyant le nombre de piles et de faces obtenu. 




	

    
  	
2

    a) Faire fonctionner ce programme pour n = 10, n = 100 puis n = 1\:000. Tester différentes fois pour n = 10\:000.


    b) Compléter le tableau suivant avec les résultats obtenus.
    





\boldsymbol{n}10\text{100}\text{1 000}\text{10 000}
Nombre de piles
Nombre de faces

    

	

  
  c) Que remarque-t-on sur les valeurs obtenues ?
  

  

  

	

  
  
  	
3

    Expliquer en quoi cela n'est pas surprenant de trouver une telle répartition dans les résultats.

  

  

	

  

  

   
  	
4

	a) 
    Sur 1\, 000 lancers, quelle est la moyenne théorique du nombre de piles obtenu ?

  

  

	
 
  
   b) On teste le programme 30 fois pour n = 1\:000 et on relève le nombre de piles.


Sur ces 30 simulations, combien donnent un écart maximal de 100 par rapport à la
moyenne attendue ?

Aide
On pourra compléter le programme Python pour automatiser les calculs.


  

  

  

 

 

  
  c) Sur 10 lancers, quelle est la moyenne théorique du nombre de piles obtenu ?
  

  

  

	

    
  d) On teste le programme 30 fois pour n = 10 et on note le nombre de piles.

Sur ces 30 simulations, combien donnent un écart maximal de 1 par rapport à la moyenne attendue ?
  

  



  

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Bilan

  



  
  
    	Dans une situation d'équiprobabilité, que peut-on dire des fréquences observées par rapport à la moyenne théorique en fonction du nombre d'expériences réalisées ?
  

  

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.




C
Une situation non équiprobable



Objectif : Simuler une expérience dans un cas non équiprobable et observer le comportement des valeurs obtenues.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

  


  On lance un dé non équilibré à six faces numérotées de 1 à 6, ayant les caractéristiques suivantes :
  

    
  
  • la probabilité d'obtenir 3 est la même que celle d'obtenir 4 : elle est égale à \frac{1}{10} ;
    • 
  
  • la probabilité d'obtenir une autre face est égale à \frac{1}{5}.
    • 




On lance le dé et on appelle \text{X} la variable aléatoire qui prend comme valeur le résultat du dé obtenu.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

	





  
  	
1

    a) 
    Donner toutes les valeurs possibles pour \text{X}.

  

  


   
    b) 
    Montrer que la situation décrit bien une loi de probabilité.

  

  





  
	

  	2
  

    	Alice a écrit le programme ci-contre pour simuler cette expérience.

Elle lance son programme pour n = 10\:000 et obtient les résultats suivants.



      




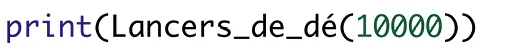
Placeholder pour Capture d'écran de code Python : fonction print affichant le résultat de Lanceurs_de_de(10000).Capture d'écran de code Python : fonction print affichant le résultat de Lanceurs_de_de(10000).



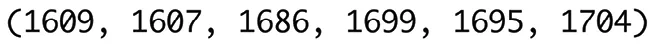
Placeholder pour Capture d'écran: suite de nombres Python (1609, 1607, 1686, 1699, 1695, 1704)Capture d'écran: suite de nombres Python (1609, 1607, 1686, 1699, 1695, 1704)








 

Justifier que le programme d'Alice n'est pas correct.
  












  	
3

    a) 
    Modifier le programme d'Alice pour simuler correctement l'expérience.

    b) Exécuter ce nouveau programme
pour n = 10, n = 100, n = 1\:000 et enfin
n = 10\:000. Noter les valeurs obtenues
dans un tableau.

Aide
Modifier les arguments de \text{randint} pour prendre en compte les probabilités et ajuster alors les conditions du  \text{if}.


   
 
n=10n=100n=1\:000n=10\:000
 1
 2
 3
 4
 5
 6
 


 

 

 

 
from random import randint

def Lancers_de_de(n):
  # n correspond au nombre de lancers effectues.
  # On initialise le nombre de faces obtenues :
  F1 = 0
  F2 = 0
  F3 = 0
  F4 = 0
  F5 = 0
  F6 = 0
  # on effectue n lancers :
  for i in range(n):
    # on simule le lancer du de à 6 faces :
    X = randint(1,6)
    # on comptabilise les resultats obtenus :
    if X == 1:
      F1 = F1 + 1
    elif X == 2:
      F2 = F2 + 1
    elif X == 3:
      F3 = F3 + 1
    elif X == 4:
      F4 = F4 + 1
    elif X == 5:
      F5 = F5 + 1
    else:
      F6 = F6 + 1
  # on renvoie le nombre de resultats obtenus :
  return(F1, F2, F3, F4, F5, F6)

print(Lancers_de_de(10000))



 
 
 


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Bilan

  

  
  
    	Dans une situation sans équiprobabilité, que peut-on dire des fréquences observées par rapport aux calculs théoriques en fonction du nombre d'expériences réalisées ?
  

  

Page suivante
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille