Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 14
TP INFO 1
Une approximation de \pi par la loi des grands nombres
16 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Dans un repère orthonormé \text{(O ; I , J)}, on considère les points d'abscisses
et d'ordonnées positives, appartenant au quart de disque \mathcal{D} délimité par
le quart de cercle \mathcal{C} de centre \text{O} et de rayon 1 ci-contre.
Une équation de \mathcal{C} est alors donnée par x^2 + y^2 = 1, où x et y sont des réels compris entre 0 et 1.
On considère l'expérience suivante :
On simule aléatoirement le positionnement de points de coordonnées (x \:; y), où (x \:; y) \in[0 \:; 1] \times[0 \:; 1]. On note \text{X} la variable aléatoire donnant le nombre de points appartenant à \mathcal{D}. Questions préliminaires :
Le cours sur la loi des grands nombres indique que la moyenne empirique peut être considérée comme un bon estimateur de \frac{\pi}{4} (pour un nombre de simulations importantes).
On considère un point de coordonnées positives appartenant au carré de côté 1 et dont \text{O}, \text{I} et \text{J} sont trois sommets.
Calculer la probabilité que ce point appartienne à \mathcal{D}.
On considère l'expérience suivante :
On simule aléatoirement le positionnement de points de coordonnées (x \:; y), où (x \:; y) \in[0 \:; 1] \times[0 \:; 1]. On note \text{X} la variable aléatoire donnant le nombre de points appartenant à \mathcal{D}. Questions préliminaires :
Le cours sur la loi des grands nombres indique que la moyenne empirique peut être considérée comme un bon estimateur de \frac{\pi}{4} (pour un nombre de simulations importantes).
On considère un point de coordonnées positives appartenant au carré de côté 1 et dont \text{O}, \text{I} et \text{J} sont trois sommets.
Calculer la probabilité que ce point appartienne à \mathcal{D}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
En utilisant la loi des grands nombres, donner une approximation de \boldsymbol{\pi} à l'aide d'une des deux méthodes.
Objectif
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Python
On considère le programme incomplet ci-dessous, écrit en Python. On suppose que n est un entier naturel strictement positif.
from math import * ... def estimateur_Pi(n): Compteur = 0 : for i in range (...): x = random() y = random() r = ... if r <= 1: Compteur = ... Prop = Compteur/n return 4*Prop
1. Compléter les pointillés.
2. Quel est le rôle de la variable \text{Compteur} ?
3. Expliquer la formule de la variable \text{Prop}.
4. Tester le programme pour différentes valeurs de n et conclure à l'aide du cours.
2. Quel est le rôle de la variable \text{Compteur} ?
3. Expliquer la formule de la variable \text{Prop}.
4. Tester le programme pour différentes valeurs de n et conclure à l'aide du cours.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
On considère la feuille de calcul suivante, permettant
de simuler l'expérience décrite dans l'énoncé.
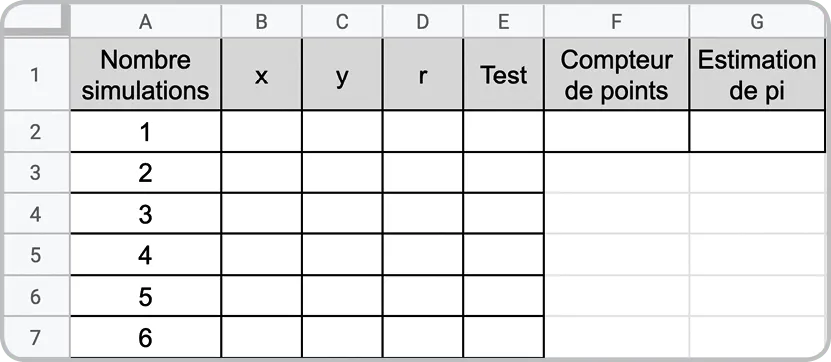1. En utilisant la commande \text{=ALEA()}, simuler des valeurs de x et de y aléatoirement sur la ligne 2.
2. Donner la formule à mettre en D2 pour calculer la distance à l'origine du point de coordonnées (x \:; y).
Le zoom est accessible dans la version Premium.
2. Donner la formule à mettre en D2 pour calculer la distance à l'origine du point de coordonnées (x \:; y).
3. Recopier et compléter la commande à mettre en
E2 : =\text{SI}(\text{D}2…\:;1\: ;0).
4. Compléter F2 afin d'avoir le compteur de test, sachant que l'on va faire 500 simulations.
5. Expliquer comment approcher la valeur de \pi. Compléter alors la case G2 avec la bonne formule.
6. Tester ce procédé pour 500 points et conclure.
4. Compléter F2 afin d'avoir le compteur de test, sachant que l'on va faire 500 simulations.
5. Expliquer comment approcher la valeur de \pi. Compléter alors la case G2 avec la bonne formule.
6. Tester ce procédé pour 500 points et conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer une valeur approchée de l'intégrale \displaystyle\int_{0}^{1} \sqrt{1-x^{2}} \text{d} x.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah